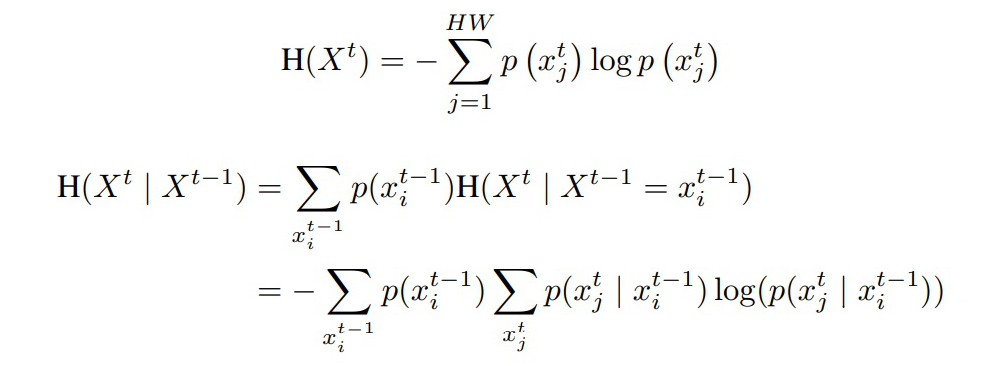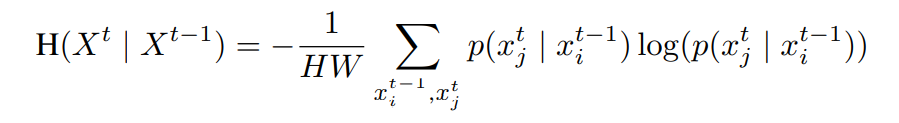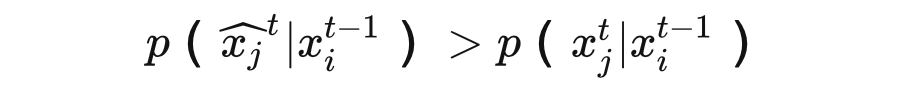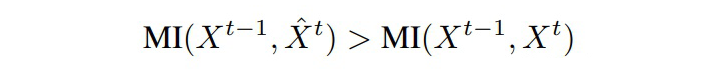NeurIPS 2022 | 基于对齐引导时间注意力机制的视频动作识别
©作者 | 张海涛
单位 | 重庆邮电大学
研究方向 | 视频理解
论文链接:

引言
1.1 问题与动机

1.2 解决方案


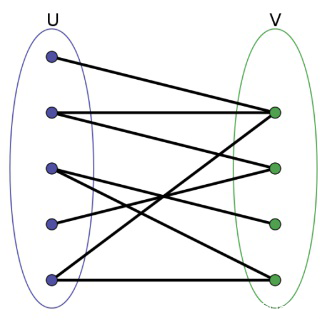
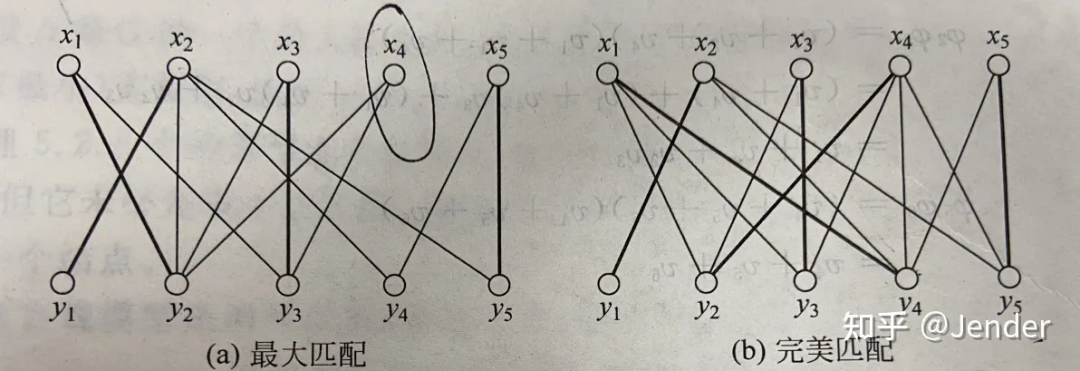
交错路径和增广路径:给定 G 的一个匹配 M,若路径 P 的边交替出现 M 中的边和非 M 中的边,则称 P 是交错路径。给定一个交错路径 P,它的起始点都是非饱和点则称 P 为增广路径。
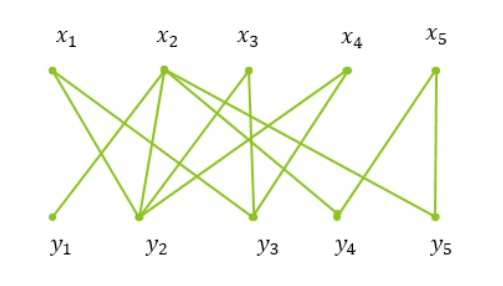
如下图,其中黑粗线表示匹配。{1,2,3}和{1,2,3,4,5}都是交错路径(一条含匹配边一条不含),但是{1,2,3}不是增广路径,因为{1,2,3}的起点(1 的左端点)是非饱和点(与匹配无关),而终点(3 的右端点)是饱和点(与匹配 4 相关)。而{1,2,3,4,5}是一条增广路径。

增广路径对匈牙利算法至关重要。从上图可以看出,{1,2,3,4,5}是一条增广路径,其中{2,4}是匹配。现在可以撤销 {2,4} 匹配,增加{1,3,5}匹配,显然{1,3,5}是不相邻的边符合匹配定义。所以,根据这条增广路径我们获得了更大的匹配。匈牙利算法目的是求解最大匹配,即图 G 不再存在 M 的增广路径。
匈牙利算法:
-
任给初始匹配 -
若 饱和 ,则是最大匹配,结束算法;否则,进入 3 -
在 点中寻找一个非饱和点 ,令 , -
若 停止,找到一个不饱和 的最大匹配;否则任选一点 -
若 是 的饱和点执行 6;否则,求从 到 的增广路径 ,执行 ,转 2 -
是 的饱和点一定存在边 ,执行 , ,转 4
例题:

顶标,它的思想是 x 取最大边的权重,y 取 0,即:
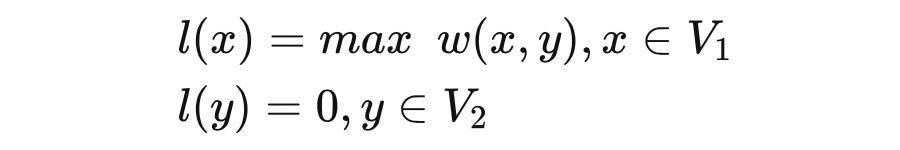

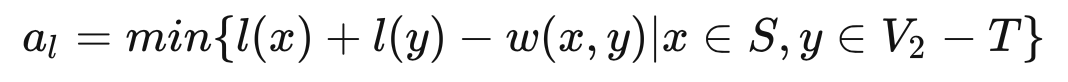

例题:

2.2 理论证明
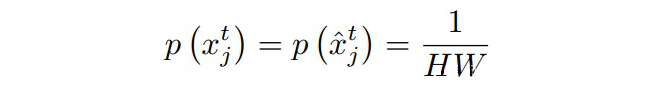
由于信息熵是负对数,则:
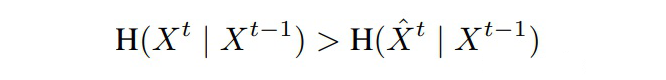
最后推导得到,对齐后的互信息更大些:
总结:对齐后相邻帧相同位置的 patch 高度相似,由于用已知信息推相似信息概率自然会大一些,所以对齐后的条件熵会小一些,那么减去小的值,互信息自然会大一些。互信息刻画了两个随机变量的相似度,在这里相邻两帧的互信息更大意味着它们在时间维度有更多的共享信息。
实验
在此不赘述论文中的所有实验,只谈谈有启发性的实验。
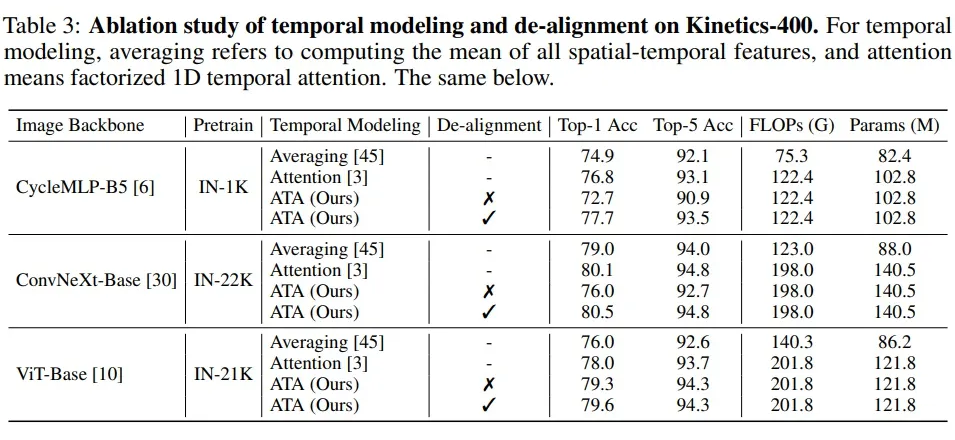
ATA 的通用性和 de-aligment 的有效性:
首先可以看出,ATA 在 MLP,Convolution,ViT 架构中都有效果。其次在时间建模方面,ATA 要远超 Averaging,略好与 Attetion。由于 Attention 建立了帧与帧间的全局联系,那么它包含的互信息也是较大的(Attention 其实也是一种对齐方法),这说明了增大互信息确实能够更好地理解视频。
另外可以观察到,在 MLP 和 Conv 架构中使用 de-alignment 的效果和不使用的效果差异明显,这是因为 MLP 和 Conv 依赖于局部的空间模式,需要空间结构的完整性。而在 ViT 架构中,不使用 de-alignment 的效果差异并不大,这是因为 Transformer 能建立全局的空间联系,对于空间结构的破坏具有一定的容忍度。
互信息比较:

明显看到,没有任何时序建模时,互信息极低。简单,增加 Averaging 后互信息剧增,这说明时序建模的有效性可能就是因为增大了相邻帧的互信息。另外,ATA 的互信息略微高于 Attention,而且 ATA 是没有参数的,说明其优势。最重要的是验证了,Aligment 确实可以增加相邻帧的互信息,并且使得分类效果更好。
总结
本文的核心思想是将相邻帧的 Token 或 Patch 对齐,即将高度相似的 Patch/Token 放在相同位置上。
这种方法,从信息论的角度是增大了互信息,从直觉来说是让相邻帧在时间维度共享更多有用的语义信息。
考虑是否用可学习的方式求解完全二部图的最优匹配并降低时间复杂度。
更多阅读



#投 稿 通 道#
让你的文字被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个,让知识真正流动起来。
📝 稿件基本要求:
• 文章确系个人原创作品,未曾在公开渠道发表,如为其他平台已发表或待发表的文章,请明确标注
• 稿件建议以 markdown 格式撰写,文中配图以附件形式发送,要求图片清晰,无版权问题
• PaperWeekly 尊重原作者署名权,并将为每篇被采纳的原创首发稿件,提供业内具有竞争力稿酬,具体依据文章阅读量和文章质量阶梯制结算
📬 投稿通道:
• 投稿邮箱:hr@paperweekly.site
• 来稿请备注即时联系方式(微信),以便我们在稿件选用的第一时间联系作者
• 您也可以直接添加小编微信(pwbot02)快速投稿,备注:姓名-投稿
△长按添加PaperWeekly小编
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧