AI能证明数学数据库中82%的问题了，新SOTA已达成，还是基于Transformer

明敏 发自 凹非寺
量子位 | 公众号 QbitAI

不得不说，科学家们最近都在痴迷给AI补数学课了。

这不，脸书团队也来凑热闹，提出了一种新模型，能完全自动化论证定理，并显著优于SOTA。

要知道，随着数学定理愈加复杂，之后再仅凭人力来论证定理只会变得更加困难。

因此，用计算机论证数学定理已经成为一个研究焦点。

此前OpenAI也提出过专攻这一方向的模型GPT-f，它能论证Metamath中56%的问题。

而这次提出的最新方法，能将这一数字提升到82.6%。

与此同时，研究人员表示该方法使用的时间还更短，与GPT-f相比可以将计算消耗缩减到原本的十分之一。

难道说这一次AI大战数学，是要成功了？

还是Transformer

本文提出的方法为一种基于Transformer的在线训练程序。

大致可以分为三步：

第一、在数学证明库中预训练；

第二、在有监督数据集上微调策略模型；

第三、在线训练策略模型和判断模型。

具体来看是利用一种搜索算法，让模型在已有的数学证明库中学习，然后去推广证明更多的问题。

其中数学证明库包括3种，分别是Metamath、Lean和自研的一种证明环境。

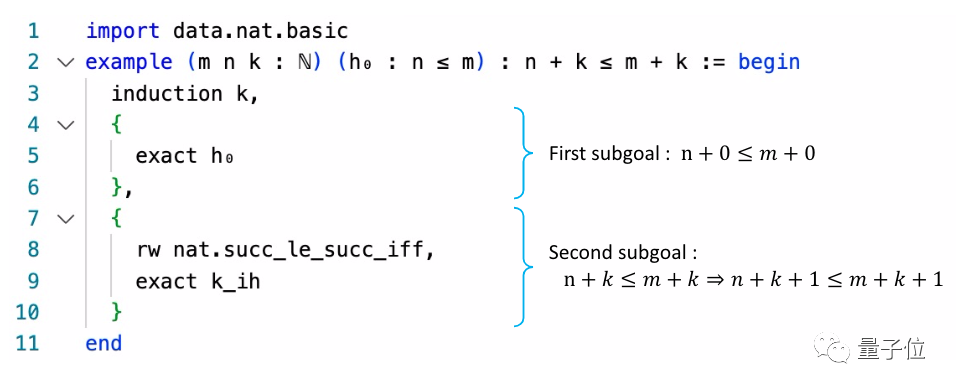
这些证明库简单来说，就是把普通数学语言转换成近似于编程语言的形式。

Metamath的主库是set.mm，包含基于ZFC集合论的约38000个证明。

Lean更为人熟知的，是微软那个可以参加IMO赛事的AI算法。Lean库就是为了教会同名算法所有的本科数学知识，并让它学会证明这些定理。

这项研究的主要目标，是为了构建一个证明器，让它可以自动生成一系列合适的策略去论证问题。

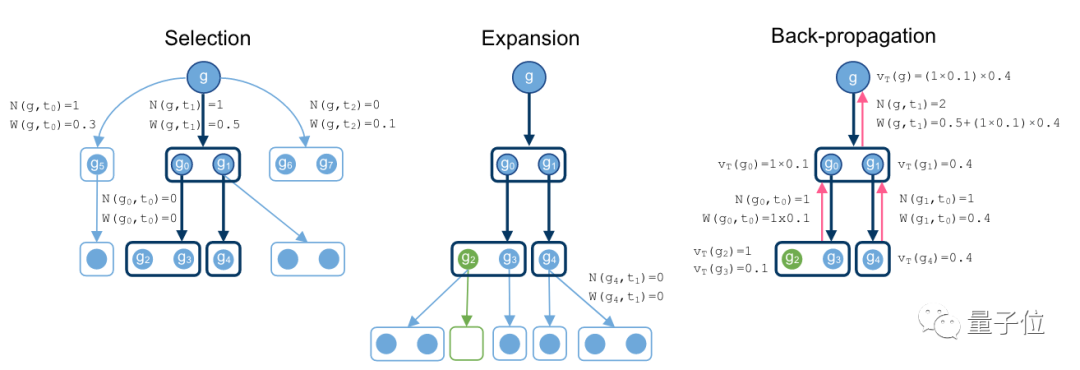
为此，研究人员提出了一个基于MCTS的非平衡超图证明搜索算法。

MCTS译为蒙特卡洛树搜索，常用于解决博弈树问题，它因为AlphaGo所被人熟知。

它的运行过程，就是通过在搜索空间中随机抽样来找寻有希望的动作，然后根据这个动作来扩展搜索树。

本项研究采用的思路类似于此。

搜索证明过程从目标g开始，向下搜索方法，逐步发展成一个超图（Hypergraph）。

当出现一个分支下出现空集时，就意味着找到了一个最优证明。

最后，在反向传播过程中，记下超树的节点值和总操作次数。

在这个环节中，研究人员假设了一个策略模型和一个判断模型。

策略模型允许判断模型进行抽样，判断模型可以评估当前策略找到证明方法的能力。

整个搜索算法，就以如上两个模型作为参照。

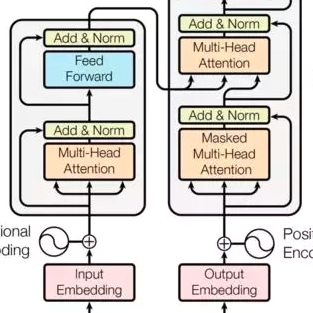
而这两个模型都是Transformer模型，且权值共享。

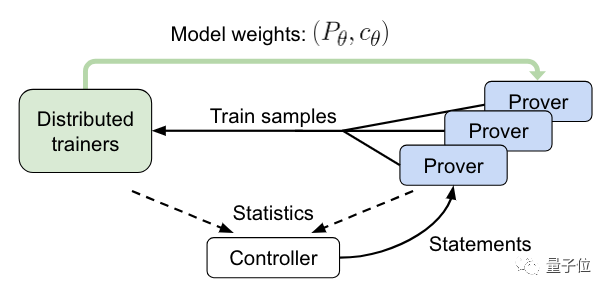
接下来，就到了在线训练的阶段。

这个过程中，控制器会将语句发送给异步HTPS验证，并收集训练和证明数据。

然后验证器会将训练样本发送给分布式训练器，并定期同步其模型副本。

实验结果

在测试环节，研究人员将HTPS与GPT-f进行了比较。

后者是OpenAI此前提出的数学定理推理模型，同样基于Transformer。

结果表明，在线训练后的模型可以证明Metamath中82%的问题，远超GPT-f此前56.5%的记录。

在Lean库中，这一模型可以证明其中43%的定理，比SOTA提高了38%，以下是该模型证明出的IMO试题。

不过目前它还不是十全十美。

比如在如下这道题中，它解题用了比原题简便的办法，但这是不对的，研究人员表示这是因为注释中出现了错误。

One More Thing

用计算机论证数学问题，四色定理的证明便是最为人熟知的例子之一。

四色定理是近代数学三大难题之一，它提出“任何一张地图只用四种颜色就能使具有共同边界的国家，着上不同的颜色”。

由于这一定理的论证需要大量计算，在它被提出后100年内，都没有人能完全论证。

直到1976年，在美国伊利诺斯大学两台计算机上，经过1200小时、100亿次判断后，终于可以论证任何一张地图都只需要4种颜色来标记，由此也轰动了整个数学界。

加之随着数学问题愈加复杂，用人力来检验定理是否正确也变得更加困难。

近来，AI界也把目光逐步聚焦在数学问题上。

2020年，OpenAI推出数学定理推理模型GPT-f，可用于自动定理证明。

这一方法可完成测试集中56.5%的证明，超过当时SOTA模型MetaGen-IL30%以上。

同年，微软也发布了可以做出IMO试题的Lean，这意味着AI能做出没见过的题目了。

去年，OpenAI给GPT-3加上验证器后，做数学题效果明显好于此前微调的办法，可以达到小学生90%的水平。

今年1月，来自MIT+哈佛+哥伦比亚大学+滑铁卢大学的一项联合研究表明，他们提出的模型可以做高数了。

总之，科学家们正在努力让AI这个偏科生变得文理双全。

论文地址：
https://arxiv.org/abs/2205.11491

— 完 —

「人工智能」、「智能汽车」微信社群邀你加入！

欢迎关注人工智能、智能汽车的小伙伴们加入我们，与AI从业者交流、切磋，不错过最新行业发展&技术进展。

ps.加好友请务必备注您的姓名-公司-职位哦~

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见~