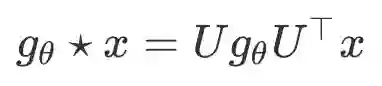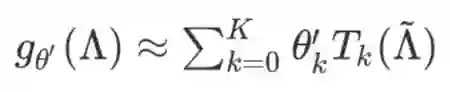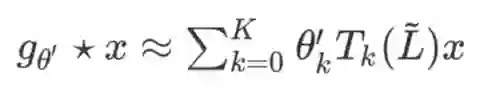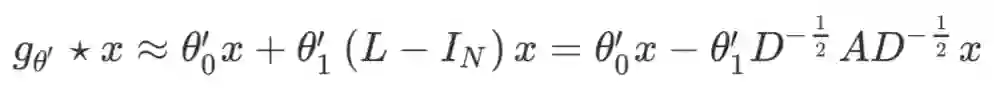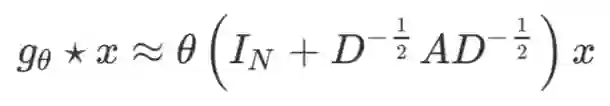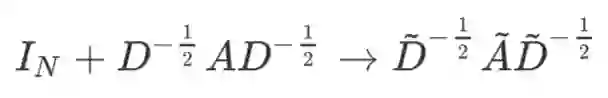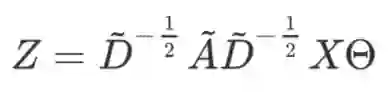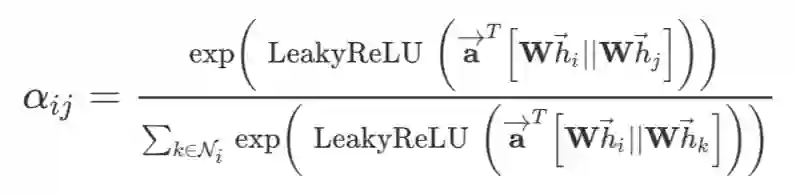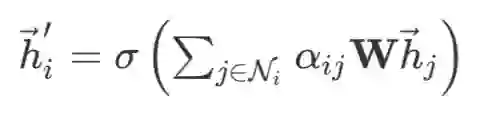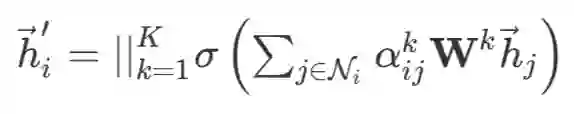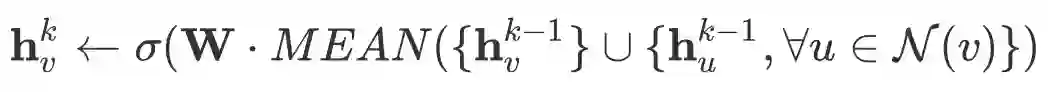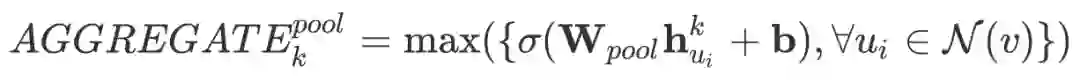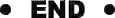图神经网络三剑客：GCN、GAT与GraphSAGE

©PaperWeekly 原创 · 作者｜桑运鑫

学校｜上海交通大学

研究方向｜图神经网络在金融领域的应用

2019 年号称图神经网络元年，在各个领域关于图神经网络的研究爆发式增长。本文主要介绍一下三种常见图神经网络：GCN、GAT 以及 GraphSAGE。前两者是目前应用比较广泛的图神经网络，后者则为图神经网络的工程应用提供了基础。

GCN

图神经网络基于巴拿赫不动点定理提出，但图神经网络领域的大发展是在 2013 年 Bruna 提出图上的基于频域和基于空域的卷积神经网络后。

关于图卷积神经网络的理解与介绍，知乎上的回答已经讲的非常透彻了。

如何理解 Graph Convolutional Network (GCN)？

https://www.zhihu.com/question/54504471/answer/332657604

这里主要介绍一下 PyG 和 DGL 两个主要的图神经网络库实现所基于的文章 Semi-supervised Classification with Graph Convolutional Networks。它基于对图上频域卷积的一阶近似提出了一种高效的逐层传播规则。 

论文标题： Semi-supervised Classification with Graph Convolutional Networks

论文链接： https://arxiv.org/abs/1609.02907

在将定义在欧式空间上的拉普拉斯算子和傅里叶变换对应到图上之后，图上的频域卷积操作可以基于卷积定理自然导出：

其中图上的拉普拉斯矩阵（归一化后）L 是一个半正定对称矩阵，它具有一些良好的性质，可以进行谱分解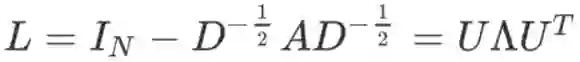：，其中 U 是 L 的特征向向量组成的矩阵，Λ 是 L 的特征值组成的对角矩阵， 则是定义在图上的对信号  的傅里叶变换。

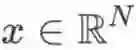
而对角矩阵  则是卷积核，也是不同的卷积操作关注的焦点，对  不同的设计会影响卷积操作的效率，其编码的信息也会影响最终任务的精度。

一开始的图卷积神经网络将  视作 L 的特征值的一个函数 。但这种定义存在两个问题： 

1. 对特征向量矩阵 U 的乘法操作时间复杂度是 ；  

2. 对大规模图的拉普拉斯矩阵 L 的特征分解是困难的。

之后的研究发现可以使用切比雪夫多项式来对 进行近似：

其中 。 是 L 的最大特征值， 是切比雪夫多项式的系数向量。切比雪夫多项式通过如下的递推公式定义：，起始值：。将其代入之前定义的卷积操作：

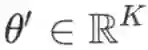
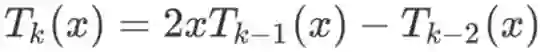
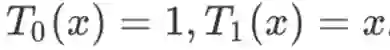
其中 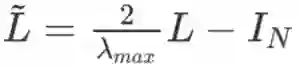，此时的时间复杂度为 。文章在此基础上对卷积操作进行了进一步的简化，首先固定 K=1，并且让  近似等于 2（注意之前对 L 的定义），则上式可以简化为一个包含两个自由参数  和  的公式：

我们进一步假定 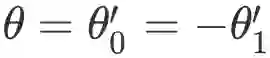，则可进一步对公式进行变形：

但是此时的  的特征值取值在 [0, 2]，对这一操作的堆叠会导致数值不稳定以及梯度爆炸（或消失）等问题。为了解决这一问题，引入一种称为重归一化（renormalization）的技术：

最后将计算进行向量化，得到最终的卷积计算公式为：

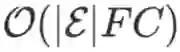
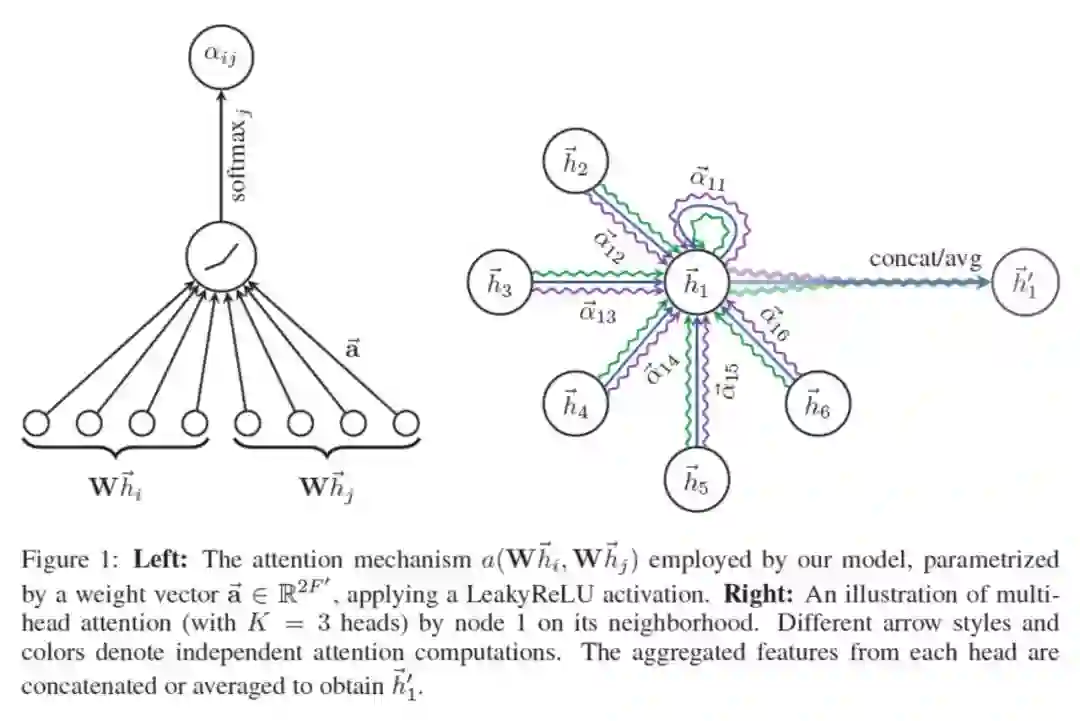
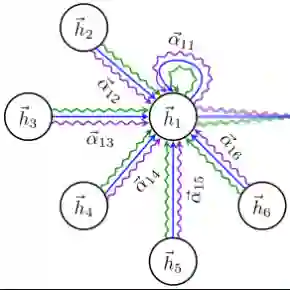
这一计算的时间复杂度为 。基于上式实现的 GCN 在三个数据集上取得了当时最好的结果。

GAT

PyG 与 DGL 的 GAT 模块都是基于 Graph Attention Networks 实现的，它的思想非常简单，就是将 transform 中大放异彩的注意力机制迁移到了图神经网络上。

论文标题：Graph Attention Networks

论文链接： https://arxiv.org/abs/1710.10903

整篇文章的内容可以用下面一张图来概况。

首先回顾下注意力机制的定义，注意力机制实质上可以理解成一个加权求和的过程：对于一个给定的 query，有一系列的 value 和与之一一对应的 key，怎样计算 query 的结果呢？

很简单，对 query 和所有的 key 求相似度，然后根据相似度对所有的 value 加权求和就行了。这个相似度就是 attention coefficients，在文章中计算如下：

其中 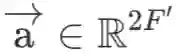 是前馈神经网络的权重系数，|| 代表拼接操作。

利用注意力机制对图中结点特征进行更新：

既然得到了上式，那么多头注意力的更新就不言而明了，用 k 个权重系数分别得到新的结点特征之后再拼接就可以了：

最后就是大家喜闻乐见的暴打 benchmarks 的环节，GAT 在三个数据集上达到了当时的 SOTA。

GraphSAGE

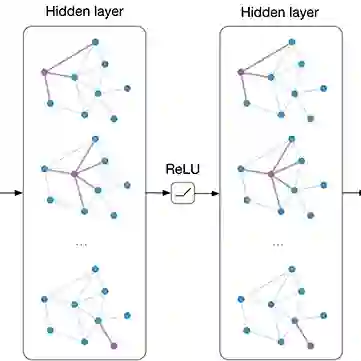
GraphSAGE 由 Inductive Representation Learning on Large Graphs 提出，该方法提供了一种通用的归纳式框架，使用结点信息特征为未出现过的（unseen）结点生成结点向量，这一方法为后来的 PinSage（GCN 在商业推荐系统首次成功应用）提供了基础。

论文标题： Inductive Representation Learning on Large Graphs

论文链接： https://arxiv.org/abs/1706.02216

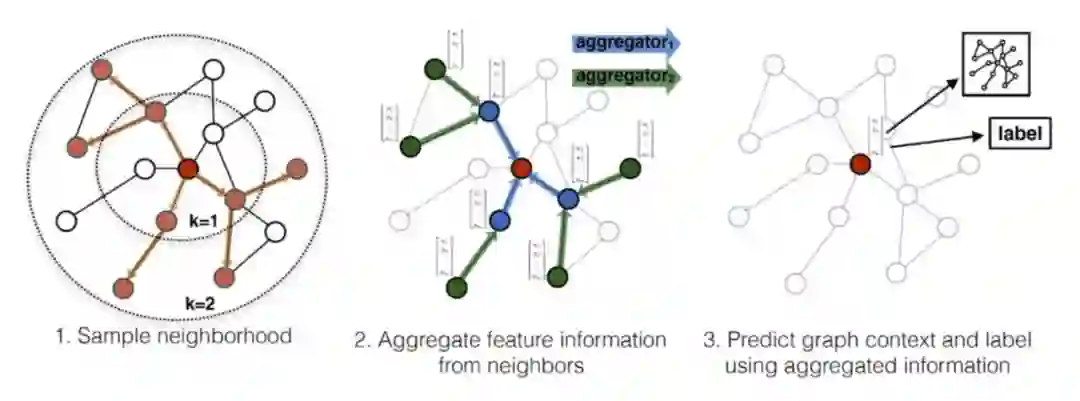
但 GraphSAGE 的思想却非常简单，也可以用一张图表示。 

算法的详细过程如下：

1. 对图上的每个结点 v，设置它的初始 embedding  为它的输入特征 ；

2. 之后进行 K次迭代，在每次迭代中，对每个结点 v，聚合它的邻居结点（采样后）的在上一轮迭代中生成的结点表示  生成当前结点的邻居结点表示 ，之后连接  输入一个前馈神经网络得到结点的当前表示  ；           

3. 最后得到每个结点的表示 。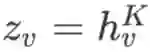

这个算法有两个关键点：一是邻居结点采样，二是聚合邻居结点信息的聚合函数。 

邻居结点采样方面，论文中在 K 轮迭代中，每轮采样不同的样本，采样数量为 。在聚合函数方面，论文提出了三种聚合函数：

Mean aggregator：

LSTM aggregator：使用 LSTM 对邻居结点信息进行聚合。值得注意地是，因为 LSTM 的序列性，这个聚合函数不具备对称性。文章中使用对邻居结点随机排列的方法来将其应用于无序集合。 

Pooling aggregator：

论文在三个数据集上取得了对于 baseline 的 SOTA。

既然为工程应用提出的方法，对于实验部分就不能一笔带过了，这里给出论文中两个有意思的结论：

对于邻居结点的采样，设置 K=2 和 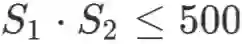 得到比较好的表现；

对于聚合函数的比较上，LSTM aggregator 和 Pooling aggregator 表现最好，但是前者比后者慢大约两倍。

总结

本文对图神经网络中常用的三种方法进行了介绍。随着图神经网络研究的热度不断上升，我们也看到图神经网络的不同变种不断涌现，此外，因为对于非欧空间数据良好的表达能力，图神经网络在交通、金融、社会科学等有大量相应数据积淀的交叉领域也面临着广阔的应用前景。

点击以下标题查看更多往期内容： 

• 针对图嵌入模型的受限黑盒对抗攻击框架
  

• 深度学习模型不确定性方法对比
  

• ICLR 2020 | 隐空间的图神经网络：Geom-GCN
  

• 深度学习预训练模型可解释性概览
  

• 如何快速理解马尔科夫链蒙特卡洛法？
  

• 神经网络中的常用激活函数总结

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。