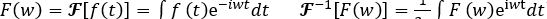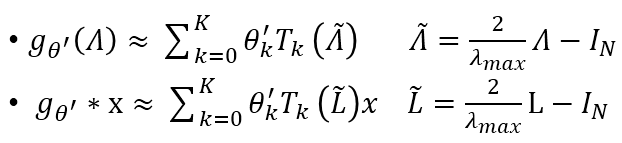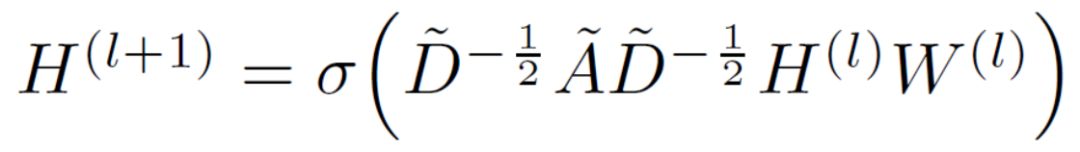图卷积网络介绍及进展【附PPT与视频资料】

2019 年 1 月 3 日 人工智能前沿讲习班

关注文章公众号

回复"王胤全"获取PPT

视频资料可点击下方阅读原文在线观看

简介

图是现实世界中一类重要的数据结构，社交网络、通讯网络、交通网络、蛋白质作用网络等都可以由图的形式表达。图的生成与分类、社区发现、节点分类等任务也有着广泛应用。近几年图卷积神经网络把深度学习中卷积神经网络的思想用到图的学习上，达到了非常好的效果。本文主要介绍图卷积网络的基本概念以及关于它的一些进展。

作者简介

王胤全，中国科学院数学与系统科学研究院硕博二年级在读，本科毕业于中国科学技术大学数学院。目前研究兴趣为图神经网络及其应用。

引言

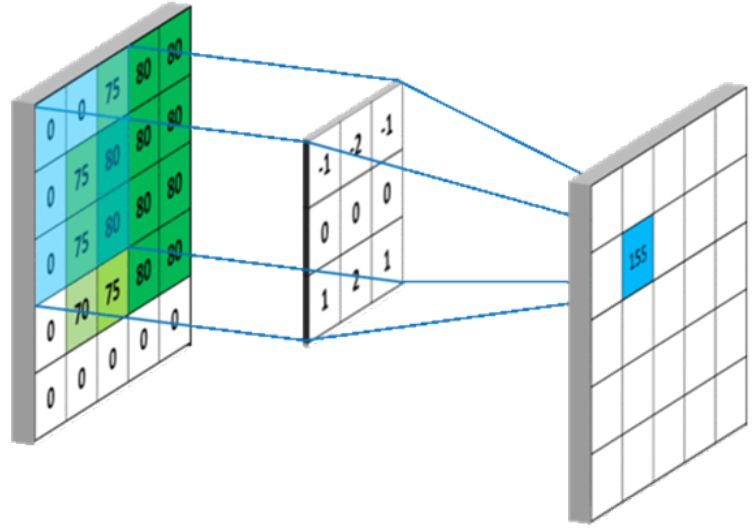
广泛应用在图像领域的CNN中使用的卷积概念是指在图像上用一个卷积核，如3*3的小矩阵在原图上以此做加权求和得到下一层的特征，这可以看做用一个像素周围的特征聚合来得到新的特征，同时也可以看做是把和卷积核结构相似的特征提取出来，即数值分布和卷积核相同时新的特征的值最大。

这种卷积操作配合pooling等在结构规则的图像等数据上效果显著，但是如果我们考虑非欧氏空间比如图(即graph，流形也是典型的非欧结构，这里我们只考虑图)，就难以选取固定的卷积核来适应整个图的不规则性，如邻居节点数量的不确定和节点顺序的不确定。

GCN就是把卷积使用在图上的一个方法，在半监督节点分类等问题上得到了很好的结果。

概念及方法介绍

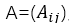
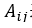
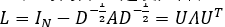
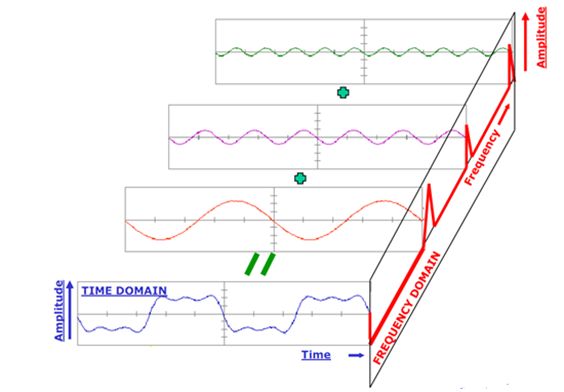
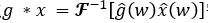
以下我们只讨论无向图，用G=(V,E)来表示一个图，其中V是顶点集，E是边集，为邻接矩阵，表示节点i，j连边的权重，对角阵D是度矩阵，对角元是每个节点的度，定义图G的拉普拉斯矩阵为，L是对称半正定的，因此可以按等式右边正交相似对角化，对角阵Λ的对角元是L的特征值，U是一个正交方阵。

卷积公式需要用到傅里叶变换，常见的傅里叶变换

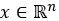
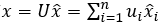
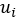
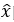
可以看做是把原函数f从时域映射到频域，如上图把一个复杂的波分解成各不相同的简单波的叠加，一个波的傅里叶变换就是这个波分解时属于不同简单波的系数。类比这种想法，对图上的一个特征或看做图信号，定义为它的傅里叶变换，用x ̂重构x时就有，其中是U的第i列向量，同时也是拉普拉斯矩阵L的特征向量，这样就把x分解成了特征向量的加权和，而后面定义的卷积也可以看做是对系数的操作。

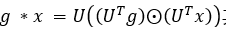
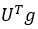
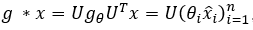
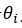
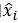
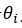
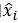
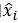
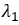
使用图的傅里叶变换，如同一般的卷积公式，两个图信号的卷积定义为其中⨀为Hadamard积，即两个向量对应元素逐点相乘，可以把Hadamard积换成点乘并把写成一个对角阵，这样卷积就变成了，由g决定系对做乘法。和图像的卷积一样，只要选择合适的卷积核g，就可以提取到想要的信号，但是由于参数的数量和点数一样多，还需要用很高复杂度求出U，并不现实。

由于只和有关，我们可以认为它是对应的特征值的函数，使用切比雪夫多项式近似即可把也写成多项式形式，同时由于是多项式函数，避免了求正交相似对角化的过程，卷积可以直接写成L的函数。

经过一些简化，一个图卷积层写成上图的形式，其中W对不同维度的特征进行变换，是网络训练的参数，而H的前面是我们定义的卷积部分。GCN用交叉熵损失函数和两层这样的网络完成图节点的半监督分类任务。

在引用网络Citeseer, Cora, Pubmed和知识图谱NELL数据集上的实验结果如图，图中数字表示分类准确率，可以看到GCN在对比的所有方法和所有数据集中均取得了最好的成绩。不仅是在半监督节点分类，在大多传统的图任务以及交通流预测、分子性质预测上也有很好的效果。

缺陷和改进

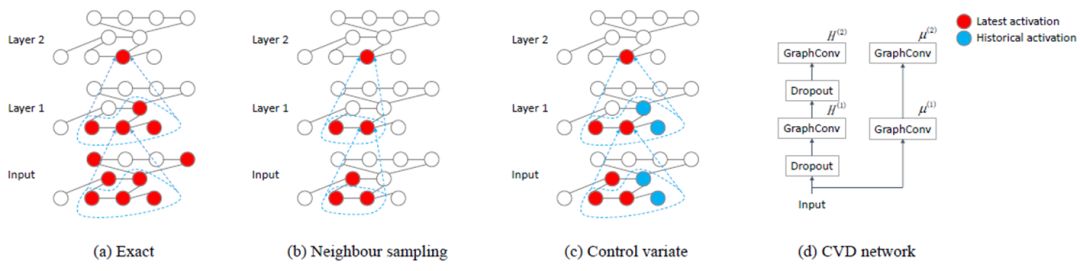
虽然GCN在应用中取得了很好的效果，它本身也存在着一些缺陷，例如训练时即使训练集很小，由于网络的特性，会有多得多的高阶邻居的信息被使用，使得对大图训练有很高的空间复杂度，文章[4]提出了一种随机训练方法避免了这一问题，并且训练效果可以和正常训练的GCN一致。即每次训练时一个节点只更新其自己和一个邻居在上一层的信息，同时使用上一层其他邻居的旧信息。

另一个问题是最终简化后的GCN的卷积核形式固定，文章[5]提出了一种方法自适应的根据任务构造新的拉普拉斯矩阵从而可以生成task-driven的不同卷积核。在多任务的数据集上取得了比原始GCN更好的效果。

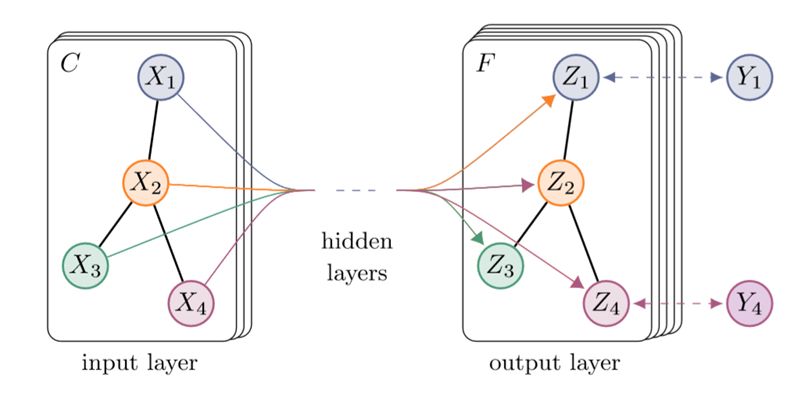
本文主要从特征值即谱的角度引入卷积，而以GraphSAGE[6]为代表的空间方法也改进了GCN的效果并且提出了更丰富的模型。

问题与挑战

虽然已有对图卷积核的改进但也并不能完全适应所有情况，求卷积核的新方法可能会改进GCN性能。

原始的GCN仅限于简单的无向图，而对动态图、异质图等复杂的图结构的学习方法也有待于提出和改进。

参考文献

[1] Defferrard, Michaël, Xavier Bresson, and Pierre Vandergheynst. "Convolutional neural networks on graphs with fast localized spectral filtering." Advances in Neural Information Processing Systems. 2016.

[2] Kipf, Thomas N., and Max Welling. "Semi-supervised classification with graph convolutional networks." arXiv preprint arXiv:1609.02907 (2016).

[3] Li, Yaguang, et al. "Diffusion convolutional recurrent neural network: Data-driven traffic forecasting." (2018).

[4] Chen, Jianfei, Jun Zhu, and Le Song. "Stochastic Training of Graph Convolutional Networks with Variance Reduction." ICML. 2018.

[5] Li, Ruoyu, et al. "Adaptive Graph Convolutional Neural Networks." arXiv preprint arXiv:1801.03226 (2018).

[6] Hamilton, Will, Zhitao Ying, and Jure Leskovec. "Inductive representation learning on large graphs." Advances in Neural Information Processing Systems. 2017.

SFFAI讲者招募

为了满足人工智能不同领域研究者相互交流、彼此启发的需求，我们发起了SFFAI这个公益活动。SFFAI每周举行一期线下活动，邀请一线科研人员分享、讨论人工智能各个领域的前沿思想和最新成果，使专注于各个细分领域的研究者开拓视野、触类旁通。

SFFAI目前主要关注机器学习、计算机视觉、自然语言处理等各个人工智能垂直领域及交叉领域的前沿进展，将对线下讨论的内容进行线上传播，使后来者少踩坑，也为讲者塑造个人影响力。

SFFAI还将构建人工智能领域的知识树（AI Knowledge Tree），通过汇总各位参与者贡献的领域知识，沉淀线下分享的前沿精华，使AI Knowledge Tree枝繁叶茂，为人工智能社区做出贡献。

这项意义非凡的社区工作正在稳步向前，衷心期待和感谢您的支持与奉献！

有意加入者请与我们联系：wangxl@mustedu.cn