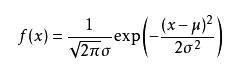干货|一文搞懂极大似然估计

推荐阅读时间：5min~8min

主要内容：通俗讲解极大似然估计

极大似然估计，通俗理解来说，就是在假定整体模型分布已知，利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

可能有小伙伴就要说了，还是有点抽象呀。我们这样想，一当模型满足某个分布，它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下：

如果我通过极大似然估计，得到模型中参数u和sigma的值，那么这个模型的均值和方差以及其它所有的信息我们是不是就知道了呢。确实是这样的。

极大似然估计中采样需满足一个重要的假设，就是所有的采样都是独立同分布的。

下面我通过俩个例子来帮助理解一下最大似然估计

1

例子一

别人博客的一个例子。

假如有一个罐子，里面有黑白两种颜色的球，数目多少不知，两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例，但我们不能把罐中的球全部拿出来数。

现在我们可以每次任意从已经摇匀的罐中拿一个球出来，记录球的颜色，然后把拿出来的球 再放回罐中。这个过程可以重复，我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中，有七十次是白球，请问罐中白球所占的比例最有可能是多少？

很多人马上就有答案了：70%。而其后的理论支撑是什么呢？

我们假设罐中白球的比例是p，那么黑球的比例就是1-p。因为每抽一个球出来，在记录颜色之后，我们把抽出的球放回了罐中并摇匀，所以每次抽出来的球的颜色服从同一独立分布。

这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中，七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。

如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样，我们可以得到如下表达式：

P(样本结果|Model)

　　= P(x1,x2,…,x100|Model)

　　= P(x1|Mel)P(x2|M)…P(x100|M)

　　= p^70(1-p)^30.

好的，我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数，也就是求的式中的p。

那么我们怎么来求这个p呢？按照什么标准来求这个p呢？

不同的p，直接导致P（样本结果|Model）的不同。

好的，我们的p实际上是有无数多种分布的。如下：

那么在上面p的分布条件下求出 p^70(1-p)^30为 7.8 * 10^(-31)

p的分布也可以是如下：

那么也可以求出p^70(1-p)^30为2.95* 10^(-27)

转自：机器学习算法与自然语言处理

完整内容请点击“阅读原文”