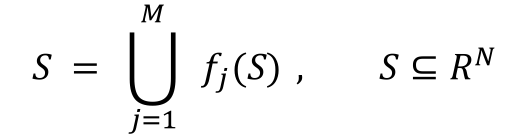花草茁壮于键盘之间——藏身数学公式中的那些美妙植物

2017 年 9 月 8 日 中国物理学会期刊网 杨夕歌

引子

不知不觉间，李雷和韩梅梅同窗已有五年了。

李雷记性很差，经常忘带作业（其实是忘了做，忘带作业受到的惩罚会小点——小编注）。但他清楚地记得，那是一个秋意乍现的早晨——树叶翠色渐退，但都不愿意落叶归根，还在同秋风做着最后的搏斗；蝉鸣鸟叫若隐若现，想来也为假期收尾而忿忿不平；就连李雷最喜欢的荷塘也沦为一潭死水，夏日里的莲花齐放蜻蜓点水总有谢幕的一天。李雷捡起一块小石子信手扔入荷塘，荷塘不情愿地泛起两层涟漪以示回礼，便没了下文。李雷低下头，神情间颇为沮丧。

不过沮丧的主要原因，是李雷“忘带”暑假作业了。

李雷不会想到，当他再次抬起头时，他的心里从此不再波澜不惊。正是那么一瞬间，猝不及防的四目相对，嫣然百媚的笑颜令李雷如痴如醉，“巧笑倩兮，美目盼兮”、“为伊消得人憔悴”、“窈窕淑女，君子好逑”甚至“十年生死两茫茫”这种一辈子都记不住的诗句如同火山爆发般喷涌而出。直到明眸巧笑随着一身纯白的轻纱渐行渐远，李雷方才反应过来，新学期开始了，该去报到了。

这位闯入李雷心窝的少女，正是五年前刚从外校转来的韩梅梅。李雷暗恋韩梅梅已有五年，应该有所行动了，因为李雷得知韩梅梅心中的白马王子——吴彦煮也就快转到他们学校了。知己知彼百战不殆，李雷偷偷跑去厕所照镜子，琢磨经反复斟酌推敲对，他认为自己颜值优势似乎并不那么明显：

失之东隅收之桑榆，好在李雷知道韩梅梅很喜欢植物，投其所好定可打动芳心！不过父母把自己的零花钱控制的很严，哪里有那么多钱去买花花草草啊。于是李雷找到了小编寻求良策。

古人“读书破万卷，下笔如有神”，到李雷这里就变成了“游戏过万关，键盘赛机枪”，是个不折不扣的游戏高手。小编推断，李雷的电脑性能定然不差，于是小编建议李雷用电脑自动画出植物的图案，打动韩梅梅芳心。小编送给李雷的第一种方案，叫做L系统，它是计算语言学的一大成果。

下面我们来具体看看什么是L系统。

第一部分 L系统——计算语言学的结晶

L系统是一种形式语法（Formal Grammar，也就是可以用 1.一个由符号构成的集合；2.数学规则表示出来的语法，是所有计算机语言的基础语法），它得名于生物学家Aristid Lindenmayer。它被广泛地用于模拟各种生物的生长过程，例如树木、藻类、酵母菌等等。

语法怎么会和生物的成长过程扯上关系呢？事实上作为形式语法的一个特例，L系统非常简单，只需要几种符号，一个数学关系式，就可以依靠迭代算法撰出惊世巨著，例如假设符号集合为S={'F', '[', ']', '+', '-'}（每个符号的意思见下文，符号的如何选择完全由读者决定），数学规则只有一个——每一次运算把字符'F'变为字符串"FF+[+F-F]-[-F+F]"。经过数次运算（迭代）以后，我们得到了个长字符串，如果把这个长字符串翻译为图像，一株类似于石松的植物遍诞生了：

石松是现存最古老的维管植物

具体代码和解释如下（小编用的python）：

# -*- coding: utf-8 -*-

from turtle import*     # 需要引入的包

t,d,n = 22,12,3     # 树枝分叉角度，树枝长度和分叉深度

F="FF+[+F-F]-[-F+F]"   # 语法形式，决定了每个树枝的形状

stack=[]   # 腾一个栈出来以储存图像

def f(n):   # 定义递归函数

  if n>0: L(F,n)

def L(s,n):   # s是字符串，n是整数

pensize(n*2)

  for c in s:   # c取遍s里面的所有字符

  if   c=='-': lt(t)   # 减号代表左转t度

  elif c=='+': rt(t)   # 加号代表右转t度

  elif c=='F': f(n-1);fd(d) # 递归并生成长度为d的树枝

  # 把当前画笔位置、角度和加（push）入栈中：

  elif c=='[': stack.append((pos(),heading(),n))

  elif c==']':   # 结束分岔

((i,j),h,p)=stack.pop()  # 读取上一个做图点的信息

penup()   # 把画笔提起来（移动时不做图）

goto(i,j)   # 画笔前往上一个做图点

seth(h)   # 设置指针朝向

pensize(p)   # 线段

pendown()   # 放下画笔（准备开始做图）

setup(480,400);speed(0);ht();penup();goto(-30,-200);pendown();seth(90)

color('green','black')   # 设置颜色

f(n)   # 开始迭代做图！

李雷看到这么一株茁壮生长的植物，不由得心花路放。绝知此事要躬行，李雷把符号集合修改成了S={'X', 'F', '[', ']', '+', '-'}，把数学规则修改为X->"FF-[[X]+X]+F[+FX]-X"和F->F，然后他得到了一颗苹果树（当然还要重新调整颜色设定）：

由数学规则生成的苹果树，迭代次数为n=4

有兴趣的读者可以尝试自己调整符号集合和数学规则，可以得到许多不同的奇妙植物的图像，例如：

这几棵树都是用很简单的L系统算法得到的。图片参考自文献[3]

甚至三维植物：

图片来自文献[3]

值得一提的是，形式语法（L系统就是形式语法的一个例子）是美国社会学家乔姆斯基（Noam Chomsky）在1950年代提出的，他创立这个概念的初衷是为了更好地研究自然语言（人类语言）。或许乔姆斯基没想到，他的理论会成为人工智能领域的奠基石。当时美苏正在争霸，因此美国人自然希望能把前苏联的科研论文批量翻译成英文；这时候又适逢计算机诞生不久，人们便琢磨着用计算机处理这个庞大的任务，一个全新交叉学科——计算语言学（Computational Linguistic）就这么横空出世了。如今各种在线翻译工具兴起，便是计算语言学的功劳。

计算语言学的例子——用递归神经网络（RNN）实现的AI写诗，引用自文献[10]。尽管诗句套路较为单一，但已有以假乱真的功力了。

在数学家眼中，形式语法无非就是自由群（Free Group）——符号集合本质上就自由群的生成元（Generator），运算规则则可以通过生成元之间的“乘法运算”来描述。利用抽象代数中的结论，人们就可以大概推算出不同的语法结构会产生怎样不同的结果了。

第二部分叶序（Phyllotaxis）是怎样炼成的

李雷兴高采烈地一步跨进教室，却发现韩梅梅已经在和吴彦煮窃窃私语了。李雷一把推开吴彦煮，把自己的杰作展示给韩梅梅看，韩梅梅又惊又喜，已然被李雷所打动。然而尚未等到芳心迁都，吴彦煮有条不地地秀出了自己模拟的向日葵：

其中每个圆圈代表一颗葵瓜子。吴彦煮的向日葵不尽惟妙惟肖，而且瓜子还变着色调，这自然令韩梅梅怦然心动。李雷不服，嚷嚷说吴彦煮这是花拳绣腿，哪里有自己的苹果树有内涵。吴彦煮微微一笑，拿出上面这张动图的代码：

# -*- coding: utf-8 -*-

from math import *

from turtle import *

def drawPhy(t, angle, size, d, petalStart):

pen(outline=1, pencolor="black", fillcolor="orange")

phi = angle * ( pi / 180.0 )

xcenter = 0.0; ycenter = 0.0

petalSize = 60   # 花瓣大小



  for n in range (0, t):

r = d * sqrt(n)   # 半径大小

theta = n * phi   # 旋转角度

x = r * cos(theta) + xcenter

y = r * sin(theta) + ycenter

fillcolor((255, theta%255, (n*4)%255))



up();setpos(x, y);down()

seth(n * angle)

  if n > petalStart-1:   # 开始画花瓣

drawPetal(x, y, petalSize)

  else: stamp()   # 否则继续画瓜子

def drawPetal(x, y, ps):   # 画菱形的花瓣

up();setpos(x, y);down()   # 初始化指针

begin_fill()

pen(outline=1, pencolor="black", fillcolor="yellow")

rt(20);fd(ps);lt(40);fd(ps);lt(140);fd(ps);lt(40);fd(ps);up()

end_fill()

colormode(255);setup(500,500);shape("circle");speed(0);ht()

drawPhy(240, 137.508, 3, 7, 200)

exitonclick()

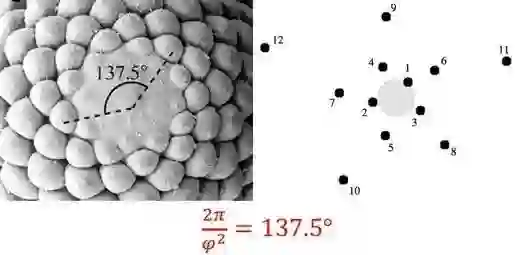
这段代码里面其实大有学问，因为如果我们把迭代函数中的角度从137.508度变为其他角度，得到的模拟结果就不再满足葵瓜子的分布图案了。植物学家们又把葵瓜子呈现出的螺旋形排列图案叫做螺旋叶序（Spiral Phyllotaxis）图案。这种螺旋图案之所以能专门冠以一个专有名词，是因为它的分布规律可以用黄金螺线（Golden Spiral）描述[4]。

黄金分割点又是斐波拉契数列相邻项的渐近比值，而葵瓜子的排列规律可以用斐波拉契数列描述

离中心最近的两颗葵瓜子之间的夹角大约呈137.5度，和黄金分割点相关

事实上叶序图案在植物界乃至整个生物界都是普遍存在的。由于叶序常常与黄金分割点相伴相随，因此黄金分割点便被赋予了美丽而又神秘的色彩。

形形色色的叶序图案

那么叶序图案是怎样产生的呢？这个问题还没有统一的答案，人们甚至还没完全弄明白向日葵螺旋叶序的产生机理。有人用能量观点（使葵瓜子之间的排斥势能最大）来解释[6]，也有人用熵的极小化原理（基于诺贝尔化学奖得主，伊利亚∙普里高津提出的耗散结构理论）来解释[7]，也有人通过生长素（Auxin）在植物器官中的分布状况来建模等等[8]。不过关于植物图案的生成机制，始终缺乏一种像由阿兰∙图灵提出的，简单却又本质的数学模型[9]（图灵提出的模型能较为本质地解释动物图案的生成，这是两个非线性发展方程，小编在《一文带你走进全球顶尖应用数学家的世界！》中已有介绍）。

第三部分山重水复疑无路？

李雷天生是个乐观主义者，经此一败后他只失望了五分钟，便又找到小编帮忙。小编也发现吴彦煮并不简单，若这样下去李雷几乎毫无胜算，必须另寻奇策。

于是小编又塞给李雷一个新的锦囊。李雷回家打开一看，里面只有六个大字：迭代函数系统（Iterated Function System）。

迭代函数系统的概念其实很简单，就是定义域和值域都是N维欧氏空间的M个收缩函数（Contraction，也就是任意两点经过函数作用后，它们的距离变短了），我们把这些函数记作f_1,f_2,...,f_M。迭代函数系统的不简单之处在于，该系统总是唯一存在一个不变集合（Fixed Set）S，使得：

该结论证明并不难，本质上就是泛函分析中压缩映照定理（Contraction Mapping Theorem，又叫Banach不动点定理）的推广。有兴趣的读者可参考文献[11]的第三节。

不变集合S长什么样呢？假设欧氏空间是2维平面，收缩函数有四个：

那么得到的不变集合S如下（采用Matlab做图，在单位正方形内随机取了20万个点，每个点迭代20次）：

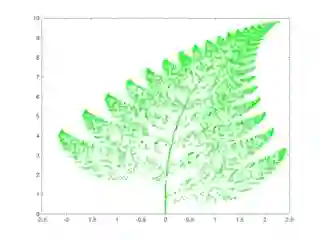
这就是蕨类植物的叶片

稍微修改一下参数，可以得到各种蕨类植物的叶片：

图片来自文献[12]

我们知道，蕨类植物是很初等的植物，器官只有根茎叶。有没有办法用迭代函数系统画出高等一些的植物呢？事实上如果我们只需要把收缩函数的个数改成六个，并适当选取参数，一颗漂亮的参天大树就跃然于屏幕上了：

这张图由10万个迭代点生成

在数学上，函数迭代系统是分形（Fractal）的一个特例。分形可谓是数学与艺术的结晶，许多由计算机生成的图像都依靠分形算法，限于篇幅这里不再展开介绍。此外，物理学家眼中的分形是自相似特性（Self Similarity）的一个体现，自相似性一个著名的例子就是海岸线悖伦（Coastline Paradox）：

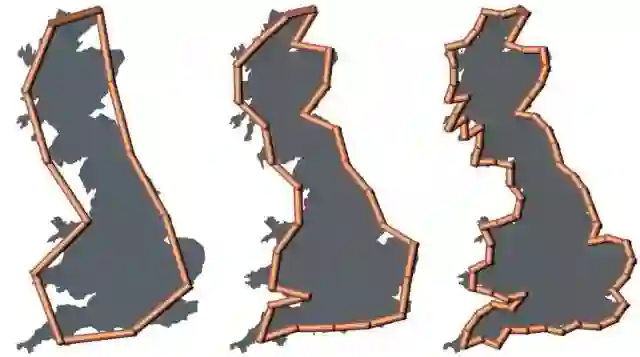
英国海岸线的长度有多长：用越细的尺度测量海岸线，得到的总长度越大，直到无穷

小编认为，蕨类植物的叶片之所以呈自相似结构，就是为了尽可能使其叶片表面积最大化，以便于叶片的光合作用。小编会在以后的文章中进一步介绍自相似性。

结语

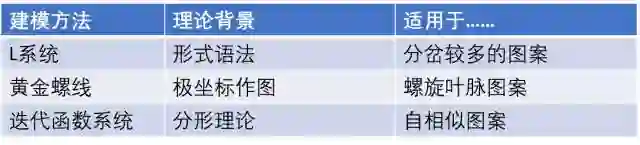
看了许多奇特的植物模拟图像，相比读者们已经大开眼界了。一饱眼福之后我们来回味一下这篇文章介绍的几种植物建模方法，大致总结如下：

有经验的读者可以从上述总结中看出，在数学上这三种建模方法都属于离散动力系统（Discrete Dynamical System）的范畴。离散动力系统用函数（或算子）的迭代代替了连续动力系统中对时间求导的过程，因而使得离散和连续动力系统的分析手段和结论存在很大差异。能不能提出一个“离散版本”的图灵模型来描述植物的形态发生过程？离散和连续动力系统这两兄弟最终能否得以相聚？这正是小编所乐见的结果。

参考文献：

[1] John Hutchins: Retrospect and prospect in computer-based translation. Proceedings of MT Summit VII, 1999.

[2] Aristid Lindenmayer, Mathematical models for cellular interaction in development, 1968.

[3] P. Prusinkiewicz and A. Lindenmayer, Algorithmic Beauty of Plants, Springer 1996.

[4] https://en.wikipedia.org/wiki/Golden_spiral

[5] S. Douady and Y. Couder, Phyllotaxis as a Physical Self-Organized Growth Process, Phys. Rev. Lett. 1992.

[6] LS. Levitov, Energetic Approach to Phyllotaxis. Europhys. Lett 1991.

[7] R. Jean, A systemic model of growth in botanometry, Journal of Theoretical Biology 1980.

[8] RS. Smith, The role of Auxin Transport in Plant Patterning Mechanisms. PLoS Biol 2008.

[9] A. Turing, The chemical basis of morphogenesis, 1952.

[10] http://www.aclweb.org/anthology/D14-1074

[11] John Hutchinson, Fractals and Self-Similarity, Indiana Univ. Math. J. 30 No. 5, 1981.

[12] T. Darmanto et. al, Metamorphic Animation of 3D Fern-like Fractal Images based on a Family of Transitional 3D IFS Code Approach, 2013 ICoICT.