数学、数学建模与人工智能之间的关系

2018 年 5 月 9 日 算法与数学之美

无论是machine larning 还是deep leraning都需要数学建模思维，没有很好地建模思维，那你的项目就达不到所谓的智能。

那么数学与建模有什么联系，我们知道在大学如果要学高数必须要学习微积分，定积分，线性代数，概率论等，所以这些都是建模的基础，建模没有对错，只有better，所以基础肯定要有的，其次要会查资料，比如各种出版论文，最新的建模思维，只要熟练掌握，那么你的建模思维就会很高级，解决实际情况的方法就会很高效。

数学与数学建模：

举个简单的列子：

如：一个星级旅馆有150个客房，经过一段时间的经营实践，旅馆经理得到了一些数据：每间客房定价为160元时，住房率为55%，每间客房定价为140元时，住房率为65%，

每间客房定价为120元时，住房率为75%，每间客房定价为100元时，住房率为85%。欲使旅馆每天收入最高，每间客房应如何定价？

[简化假设]

　　（1）每间客房最高定价为160元；

　　（2）设随着房价的下降，住房率呈线性增长；

　　（3）设旅馆每间客房定价相等。

　　[建立模型]

设y表示旅馆一天的总收入，与160元相比每间客房降低的房价为x元。由假设（2）可得，每降价1元，住房率就增加。可知

　　[求解模型]

利用二次函数求最值可得到当x=25即住房定价为135元时，y取最大值13668.75（元），

　　[讨论与验证]

　　（1）容易验证此收入在各种已知定价对应的收入中是最大的。如果为了便于管理，定价为140元也是可以的，因为此时它与最高收入只差18.75元。

　　（2）如果定价为180元，住房率应为45%，相应的收入只有12150元，因此假设（1）是合理的。

这便是一个简单的数学建模，在这道题中我们需要考虑的是：

1.要做什么？

2.怎么做？

3.这样做合理吗？

4.如果这样做，假设那些可以改变？

5.这样做需要用到那些模型？

6.这种模型简洁吗？

7.确定了这种模型，怎么求解？

8.求解出来了，与现实合理吗？

9.在这个模型中，存在什么缺点，怎么去优化？

10.总结

差不多这十点是需要我们考虑的，也许要大量用到数学计算，甚至涉及到统计，经济学，专有软件（matlab，spass）的处理等，所以整个建模过程离不了数学知识。

数学建模与人工智能：

同样通过一个小例子来理解他们之间的关系：

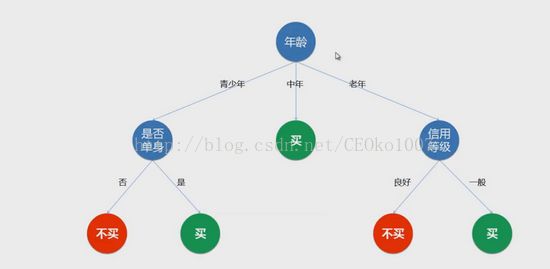
题目：在一个公司中，由于某些原因，有些员工渐渐离网（从公司流失），对于此，请用机器学习算法预测客户流失的一些特点，包括年龄，性别等其它因素。

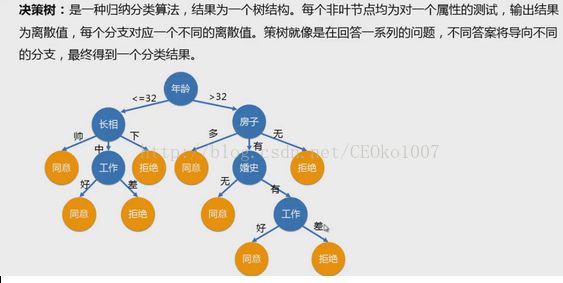
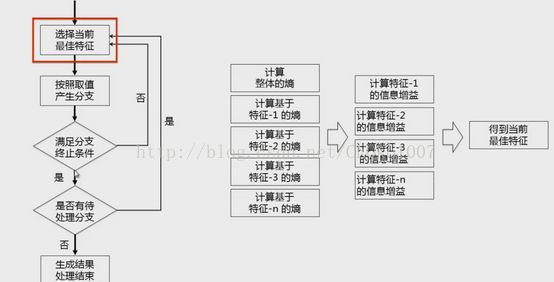
在这道题中，利用机器学习时要用到一种建模模型：决策树

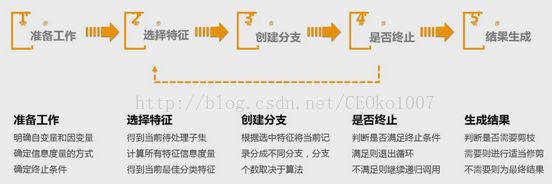
1.决策树如何构建？

2.构建决策树

3.生成决策树

4.利用ID3算法实现function

5.集成学习

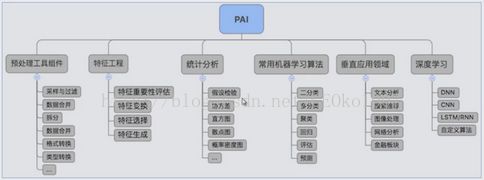
6.然后利用PAI算法执行

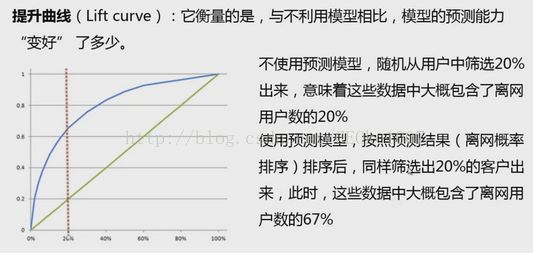
7.分析效果

8.总结

不难发现通过这复杂的八步就完美提供了解决方案，完成项目需求，而这八步都需要扎实的建模思维，要不然几乎没办法做，所以数学建模对于人工智能算法非常关键。

再者比如最新的滴滴Di-Tech算法大赛：

问题是：对无人驾驶车而言，最重要的是能够理解周围环境并做出相应决策，保证行车安全。参赛者需要努力找到通过摄像头和 LIDAR 数据检测道路上的障碍物的最好方法。最终的系统应该能够识别行人、车辆和普通障碍物，对人类驾驶员和无人驾驶系统都有很大帮助。参赛者需要处理 LIDAR、RADAR及摄像头原始数据，输出障碍物位置、移除噪音和环境错误检测。参赛者可以利用已经较为完善的 Kitti 数据集，在现有技术的基础上，加入自己的新方法和手段，来让算法获得更好表现。

不难发现无论是怎样的安全措施，数据分析，算法处理，都需要建模思维各个方面考虑，完美的建模便是最好的答案。

∑编辑 | Gemini