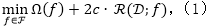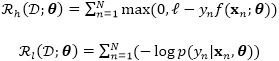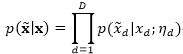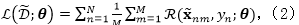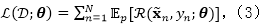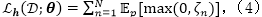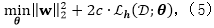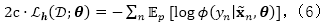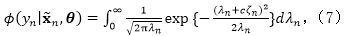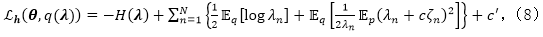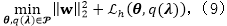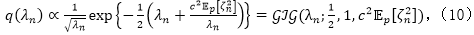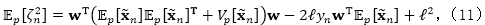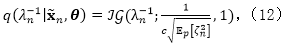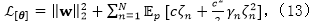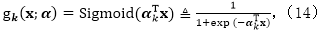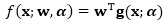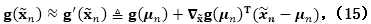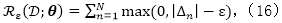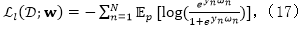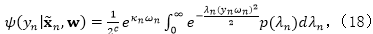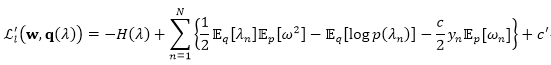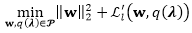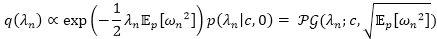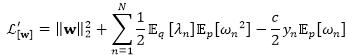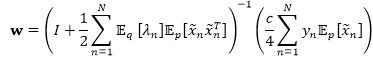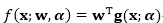FCS论文阅读笔记|利用数据增强技术针对SVM进行dropout训练
点击上方蓝字

关注我们
今天,FCS给大家分享一篇人工智能专栏论文(作者清华大学朱军老师等)——《Dropout training for SVMs with data augmentation(利用数据增强技术针对SVM进行dropout训练)》的阅读笔记,由我们的读者提供。
如果您也同样对这篇论文感兴趣,或者也想把您阅读我们期刊论文的感受分享给更多的小伙伴,欢迎在文后留言或者与我们联系。
原文信息:
Dropout training for SVMs with data augmentation
Frontiers of Computer Science,2018,12(4):694-713
Ning CHEN, Jun ZHU, Jianfei CHEN, Ting CHEN
长按识别二维码,阅读文章详情
01
简介
通过在给定训练样本的基础上增加一个固定的噪声分布,可以为有限的训练数据增加大量的损坏样本。在众多噪声机制中,dropout训练的效果十分显著。尽管对于二次损失、指数损失和从广义线性模型(GLM)中推导出来的对数损失已经有了很多研究,但是对于支持向量机(SVM)上的铰链损失的研究却很少。一个技术难题就是铰链损失的非平滑性使得计算甚至是估计它在一个给定损坏分布下的期望变得十分困难。本文试图解决这个难题并且通过拓展dropout训练和其他对于SVM的特征噪声机制来填补这一空隙。
02
背景知识
2.1 正则化损失最小化
考虑二分类问题,其中每一个训练数据(x,y)都包含一个输入特征向量
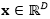
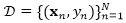
其中Ω(f)是一个正则项用来防止过拟合,c是一个非负参数。
对于线性模型而言,函数f可以简单地用参数表示为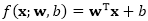
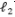
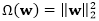
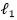
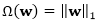
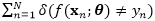
其中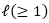
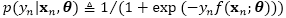
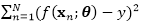
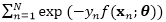
2.2 边缘化损坏学习
令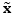
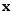
其中每个独立分布都是指数家族中的一员,自然参数是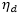
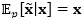
对于显式损坏,每一个数据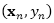
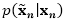
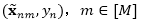
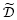
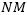
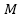
其中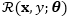
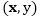
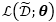
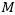
dropout训练则采用了隐式损坏的策略,通过最小化损坏分布下的损失函数的期望,利用边缘化损坏特征来训练模型。
这一目标可以看作是式(2)当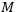
在式(3)中损失函数R的选择会显著地影响计算成本和预测的准确度。对于二次损失、指数损失、逻辑损失和从GLM中推导出来的对数损失都有了一系列研究。对于二次损失和指数损失,式(3)中的期望可以解析算出,使用简单的梯度下降算法。然而,对于计算逻辑损失和GLM对数损失的期望而言,还没有一个闭合解。之前的研究已经采取了近似方法,例如使用二阶泰勒展开或者通过使用Jensen不等式得到一个上界,这两种方法都在实践过程中产生了一个很有效的算法。与此相对的是,对于铰链损失却少有研究。我们通过下面阐述的有效算法来填补研究领域的这一空白。
03
dropout SVM
在这一部分中,我们在分类和回归两方面展示了线性SVM和利用表征学习的非线性拓展的dropout训练。
3.1 有损坏噪声的线性SVM
对于线性SVM而言,期望的铰链损失可以被写为如下形式:
其中我们定义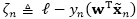
下面,我们使用一个简单的迭代重加权最小二乘(IRLS)算法来解决这个问题,包括一个期望损失的变分边界和一个可以迭代地最小化重加权二次损失期望的算法。
3.1.1 使用数据增强的变分边界
由于我们没有对于最大值函数期望的一个闭合解,直接求解式(5)非常困难。因此,我们采用了变分分析的一般框架,并且根据利用了数据增强技术的铰链损失推导出变分上界。具体来说,令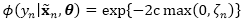
通过使用数据增强技术,我们可以将伪似然性表示为
其中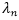
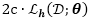
其中,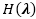
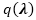
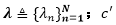
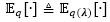
3.1.2 迭代重加权最小二乘算法
在该上界中,我们注意到对于给定变分分布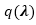
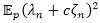
对于
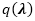
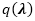
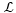
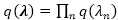
其中二阶期望为
并且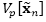

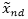
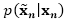
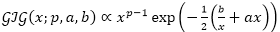
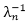
对于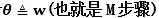
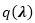
其中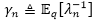
总而言之,我们的算法在给定的损坏分布下迭代地最小化一个简单重加权二次损失的期望,其中权重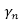
3.2 使用表征学习的dropout SVM
上面我们假设对于输入特征而言分类器是一个线性模型,现在我们通过学习一种非线性特征来放松这一假设,这种方法在表征学习中十分常见。
利用一个
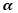
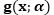
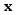
其中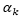
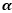
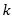
其中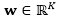
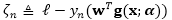
使用同样的数据增强技术,我们可以得到一个像式(8)一样的期望铰链损失的变分上界,同样是使用新定义的。然而,需要注意的是变分上界也是的一个函数,在实际处理起来很困难。这里我们使用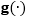
其中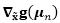
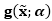
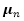
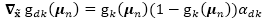
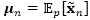
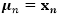
利用一阶泰勒展开,我们可以计算变分上界,然后将上面算法做一点小改动就可以得到一个针对这个问题的最小化算法。
3.3 针对回归问题的dropout SVMs
我们简单地讨论如何将以上思想拓展到回归任务中,其中因变量Y取实数值。在回归问题中,一个对于支持向量回归(SVR)模型常用的损失为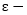
其中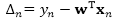
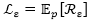
04
dropout逻辑回归
在这一部分,我们针对逻辑回归和它在分类问题上利用隐特征的拓展使用dropout训练提出了一个新的IRLS算法。这可以让我们对逻辑回归与SVM进行比较。
4.1 有损坏噪声的逻辑回归
定义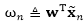
同样地,由于该期望并不存在一个闭合解,因此我们使用一个变分上界来作为替代。具体来讲,令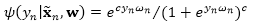
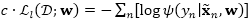
其中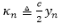
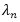
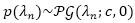
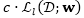
并且得到变分优化问题:
其中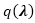
4.2 坐标下降算法
我们使用坐标下降算法来解决上述的变分问题:
对于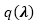
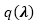
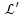
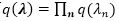
这是一个Polya-Gamma分布,其中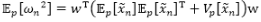
对于w(也就是M步骤) 通过固定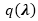
如果数据维度不是很高,那么我们可以得到这个优化问题的闭合解:
然而,如果数据是高维的,那我们就必须采用有效的数值方法,和SVMs中的类似。
4.3 使用表征学习的dropout逻辑回归
我们将逻辑回归拓展使其能在损坏学习环境中学习隐特征。具体来说,利用一个D×K维的矩阵α,我们令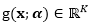
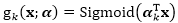
使用同样的数据增强技术,我们可以得到期望逻辑损失的一个变分上界。我们采用同样的策略利用泰勒展开在损坏特征均值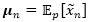
05
实验结果及对比
本文在九个数据集上将我们对于分类和回归提出的模型进行对比,包括1)Amazon review;2)Dmoz;3)Reuters);4)CIFAR;5)MNIST;6)Hotelreview。其中Amazon review包含四种类型的文本评价数据集。
5.1 线性dropout分类器
5.1.1 dropout SVM vs.显式损坏
结果表明训练集中包含的损坏样本越多(M越大),误差越小,当M趋向于无穷时,性能最好,而这也相当于dropout SVM。
5.1.2 二分类问题
将Dropout-SVM和Dropout-LR在Amazon review数据集上进行对比,与当下最好的MCF-Logistic相比,这两种算法都得到了很不错的效果,说明在SVM上的dropout训练对于二分类问题是非常有效的。
5.1.3 多分类问题
采用“一对多”的策略在DMOZ,Reuters和CIFAR-10数据集上对比Dropout-SVM和Dropout-LR。在文章分类和图片分类问题上,使用dropout训练对于分类器性能都有了很大提升,Dropout-SVM和Dropout-LR的性能都远远优于基线MCF-Quadratic,在文章分类问题上Dropout-SVM比当下最好的MCF-Logistic的性能还要稍好一些。
5.1.4 回归问题
将Dropout-SVR和MCF-Quadratic在Hotelreview数据集上进行对比,结果表明对于任何dropout水平,Dropout-SVR的性能都要优于MCF-Quadratic,表明dropout训练同样适用于回归任务。
5.2 使用表征学习的分类器
将Dropout-LatentSVM和Dropout-LatentLR在图片分类和文本分类任务上进行对比,分别使用了CIFAR-10和Amazon review数据集,都能得出dropout训练能提高分类器性能的结论,但对于文本分类而言,非线性dropout分类器与线性分类器对比并没有得到明显提升,可能是因为单词本身就已经是高维特征,或者是简单的全连接网络不适用于文本分类。
5.3 Nightmare at test time
选择MNIST数据集来训练线性的Dropout-SVM、Dropout-LR和非线性的Dropout-LatentSVM、Dropout-LatentLR,结果表明Dropout-SVM比其他任务分类器都要稳定。利用隐特征的非线性分类器比线性分类器性能要好。
除此之外,文章还对隐特征可视化,对于隐藏维度的敏感性,时间复杂度进行了分析。
06
总结
本文针对线性SVM和对SVM利用隐特征进行的非线性拓展进行了dropout训练,利用数据增强技术,使用了迭代重加权最小二乘算法(IRLS)。利用同样的思想使用一种新的IRLS算法对于逻辑回归也进行了dropout训练,进一步探究了在dropout学习中不同损失函数之间的联系与区别。在不同任务上的实验结果表明了本文提出方法的有效性。
注:本文为该读者的阅读笔记,未经原论文作者和FCS期刊审读。仅供广大读者参考。
从上下文语境中学习: 基于相互增强模型的中文微博观点检索 2018 12(4):714-724
基于样本选择的安全图半监督学习方法 2018 12(4):725-735
基于LDA模型的协同过滤 2018 12(3):571-581
Frontiers of Computer Science

长按二维码关注Frontiers of Computer Science公众号