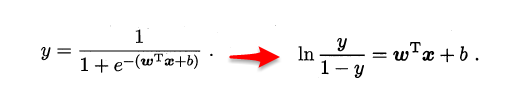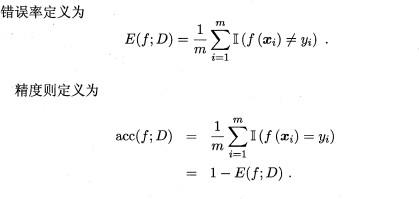赶紧收藏！西瓜书《机器学习》完整笔记来了

来自：开源最前线（ID：OpenSourceTop） 

西瓜书《机器学习》是机器学习的必读书籍。 作为该领域的入门教材，在内容上尽可能涵盖机器学习基础知识的各方面。 适合大学三年级以上的理工科本科生和研究生，以及具有类似背景的对机器学 习感兴趣的人士

虽然周志华教授已经尽可能少地使用数学知识，但是，还是没法避免必要的数学知识填充，基础较为薄弱的学生仍然觉得不好理解，这里猿妹和大家推荐一份《机器学习》的学习笔记—— Machine-learning-learning-notes

这份笔记出自一名叫Vay-keen的深圳大学学生，该笔记记录了其在学习这本书的过程中的理解思路以及一些有助于消化书内容的拓展知识。

目前，这份笔记已经在Github上获得 1421 个Star， 360 个Fork，共提交了 24 次commits（Github地址： https://github.com/Vay-keen/Machine-learning-learning-notes ）

笔记共分为17个部分，笔记的前一部分主要是对机器学习预备知识的概括，包括机器学习的定义/术语、学习器性能的评估/度量以及比较，之后将主要对具体的学习算法进行理解总结。

笔记详细到什么程序呢？ 这里我们附上一小段笔记展示：

线性回归

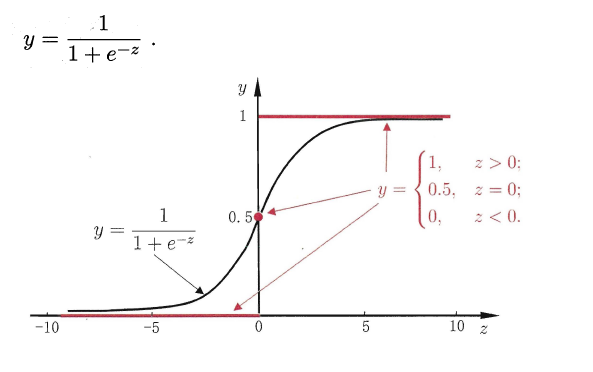
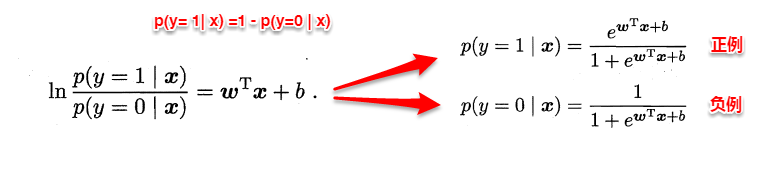
回归就是通过输入的属性值得到一个预测值，利用上述广义线性模型的特征，是否可以通过一个联系函数，将预测值转化为离散值从而进行分类呢？ 线性几率回归正是研究这样的问题。 对数几率引入了一个对数几率函数（logistic function）,将预测值投影到0-1之间，从而将线性回归问题转化为二分类问题

若将y看做样本为正例的概率，（1-y）看做样本为反例的概率，则上式实际上使用线性回归模型的预测结果器逼近真实标记的对数几率。 因此这个模型称为“对数几率回归”（logistic regression），也有一些书籍称之为“逻辑回归”。 下面使用最大似然估计的方法来计算出w和b两个参数的取值，下面只列出求解的思路，不列出具体的计算过程

最常见的性能度量

在回归任务中，即预测连续值的问题，最常用的性能度量是“均方误差”（mean squared error）,很多的经典算法都是采用了MSE作为评价函数，想必大家都十分熟悉。

在分类任务中，即预测离散值的问题，最常用的是错误率和精度，错误率是分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占样本总数的比例，易知：错误率+精度=1。

---

●编号879，输入编号直达本文

●输入m获取文章目录

推荐↓↓↓

开源最前线