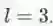网络表示学习介绍

2018 年 11 月 26 日 人工智能前沿讲习班

关注文章公众号

回复"柳阳"获取PDF资料

导读

网络数据可以自然表达物体与物体之间的联系，生活中充满了网络数据，例如社交网络、计算机网络、物流网络、学术网络等等。在有关网络的研究中，如何表示网络信息是一个重要的问题。传统方法可以利用高维稀疏向量表示网络中的一个节点，但局限在于难以度量节点之间的相似性并且还会增大模型的时间和空间复杂度。随着表示学习技术在自然语言处理领域的成熟，相关的低维稠密向量表示方法也被应用于网络数据中。本文主要对近年来比较流行的几种网络表示学习方法进行简要的梳理和总结，以方便读者选择合适的方法解决特定的问题。

作者简介

柳阳，中国科学院计算技术研究所智能信息处理重点实验室在读博士，本科毕业于南京大学。目前研究兴趣为网络表示学习应用，涉及领域有城市活动建模和区块链交易模式挖掘。

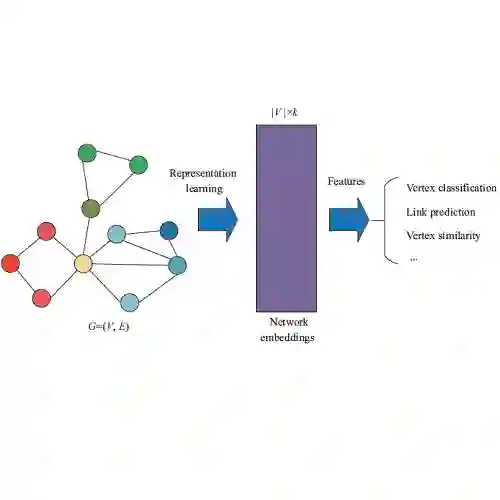
网络嵌入概述（Network Embedding）

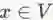
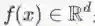
网络嵌入是学习一个映射，将网络中的节点映射到一个低维空间的稠密向量表示，即学习一个映射，是网络中的一个节点，是X的特征表示。网络按照点类型和边类型可以分为两类，同质网络中只有一种类型的节点和一种边，异质网络可能包含多种类型的节点或多种类型的边。由于网络结构存在很大的不同，相应的网络嵌入方法也被分为两类，下面将从两方面分别介绍。

同质网络嵌入（Homogeneous Network Embedding）

同质网络嵌入方法主要有4种，分别是DeepWalk, node2vec, LINE, SDNE. 其中，DeepWalk和node2vec都是基于网络上的随机游走外加Skip-gram模型进行节点嵌入，LINE和SDNE都显式地定义了相应的损失函数保持节点之间的一阶和二阶相似度。

DeepWalk

DeepWalk[1]是第一个将神经网络语言模型Word2Vec应用到网络数据中的网络表示学习方法，本质思想在于将图上的随机游走序列类比为语言模型中的句子，依据是网络中的顶点在随机游走中的出现频率与单词出现在句子中的频率都服从幂律分布。用Skip-gram模型建模随机游走序列，并使用Hierarchical Softmax进行优化，是DeepWalk的主要思想。

node2vec

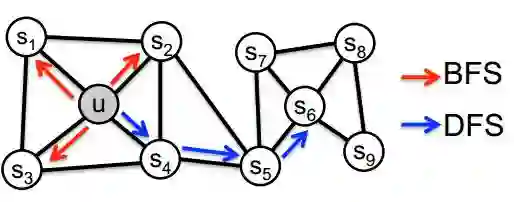
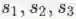
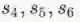
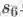
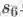
node2vec[2]改进了DeepWalk中的随机游走策略，在网络上进行游走可以有宽度优先和深度优先两种策略。宽度优先原则倾向于使得结构上更近的顶点具有相似的特征表示，深度优先的原则有利于发现具有相同结构和功能的顶点。对于下图中的顶点u，宽度优先产生的邻居节点为，深度优先产生的邻居节点为，不难看出，节点与u具有结构相似性，因此与u也应当有相似的特征表示。

LINE

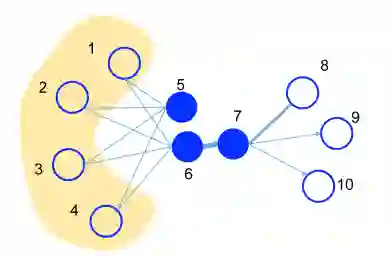
LINE[3](Large-scale Information Network Embedding)定义了节点之间的一阶相似度和二阶相似度。一阶相似度定义为两个顶点之间是否有边相连。下图中顶点6和7有连边，而5和6之间没有连边，所以在一阶相似度量下，顶点6和7更加相似。二阶相似度定义为两个顶点邻居之间的相似度，如果两个顶点的共同邻居顶点越多那么他们越相似。下图中顶点5和6具有相同的邻居节点（黄色阴影部分），而顶点6和7没有共同的邻居顶点，那么在二阶相似度量下，顶点5和6更加相似。

SDNE

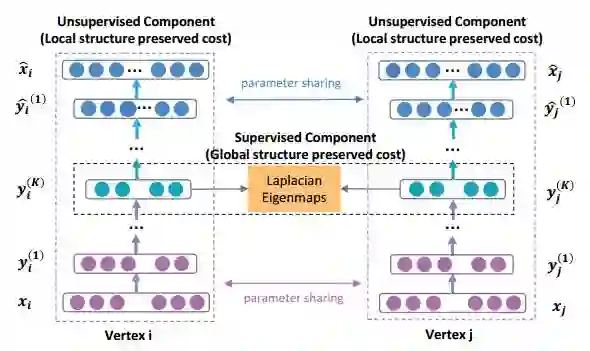
SDNE[4](Structural Deep Network Embedding)利用下图所示的深度神经网络结构学习节点的特征表示，基于自动编码机的基本结构，定义了监督和无监督两部分损失函数。自动编码机的输入是网络邻接矩阵的一行，表示一个节点和网络中其他节点的邻接关系，重构误差在于恢复节点的邻居信息，因此有利于保持二阶相似度。自动编码机的中间隐层是学习得到的特征表示，利用拉普拉斯特征映射的思想定义一阶损失，使得相似度大的节点的特征表示也尽可能接近，因此有利于保持一阶相似度。

异质网络嵌入（Heterogeneous Network Embedding）

异质网络嵌入方法有3种，分别是HIN2Vec, metapath2vec, JUST。其中，HIN2Vec是基于神经网络的嵌入方法，metapath2vec和JUST都是基于网络上的随机游走外加Skip-gram模型进行节点嵌入。

HIN2Vec

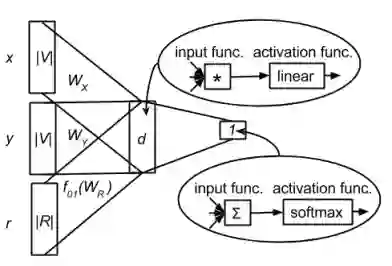
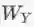
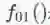
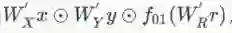
HIN2Vec[5]的网络结构如下图所示，可以理解为一个单隐层神经网络。输入X和Y为两个顶点的one-hot向量表示，维度等于顶点数量和是待学习的嵌入矩阵，r是由元路径表示的关系，是一个正则函数将关系的隐表示限制在0和1之间，隐层向量由三个向量按位相乘得到，网络的输出即为判断x和y是否具有关系r，因此可以将模型理解为一个二分类器，损失函数即为交叉熵损失。

metapath2vec

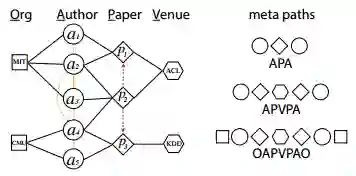
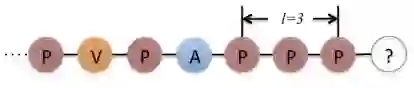
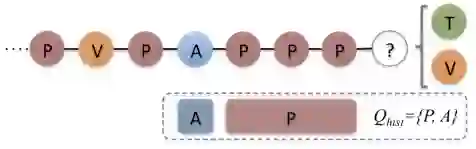
metapath2vec[6]提出了基于元路径（meta-path）的随机游走，基本框架如下图所示：

具体地，如有左下图所示的学术网络，可以定义3种元路径如右下图所示：

产生符合定义的随机游走序列，利用Skip-gram算法，可以得到顶点的嵌入向量。

JUST

JUST[7]在网络上的随机游走不依赖于预先定义好的元路径（meta-path），在进行随机游走选择下一个顶点时，可以跳（JUmp）到其他顶点类型中，也可以留（STay）在原来的顶点类型中。是去是留，需要定义好转移概率。如果与当前顶点相连的顶点没有相同类型的，那么只能选择Jump；如果相连的顶点没有不同类型的，那么只能选择Stay；除此以外，定义留在相同类型顶点的概率为指数下降，其中是初始停留概率，表示此前连续访问的同类型顶点的个数，如图所示，

如果选择跳转，需要选择目标顶点类型，定义队列为最近访问过的个顶点类型，下图中，而原图中一共有4种类型（A, P, T, V），下一步在T和V中随机选择一个。

用上述方法对每个顶点生成随机游走序列，利用Skip-gram模型，可以得到顶点的嵌入向量。

Take Home Message

DeepWalk，LINE和node2vec是3种常用的网络表示学习方法，相较于随机游走的方法DeepWalk和node2vec，LINE的运行速度较快。node2vec是DeepWalk方法的扩展，因此DeepWalk也可以理解为node2vec的一种特殊形式。对于异质网络，核心在于如何生成带有特定节点类型的随机游走序列，许多方法基于用户定义的元路径进行网络嵌入，JUST不依赖于元路径但是其自动生成的路径缺少一定的可解释性。

声明：本文中所有图片都取自相应论文，参考文献如下。

[1] Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. 2014. DeepWalk: online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD '14). ACM, New York, NY, USA, 701-710. DOI: https://doi.org/10.1145/2623330.2623732 ↩

[2] Aditya Grover and Jure Leskovec. 2016. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '16). ACM, New York, NY, USA, 855-864. DOI: https://doi.org/10.1145/2939672.2939754 ↩

[3] Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J., & Mei, Q. (2015, May). Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web (pp. 1067-1077). International World Wide Web Conferences Steering Committee. ↩

[4] Daixin Wang, Peng Cui, and Wenwu Zhu. 2016. Structural Deep Network Embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '16). ACM, New York, NY, USA, 1225-1234. DOI: https://doi.org/10.1145/2939672.2939753 ↩

[5] Tao-yang Fu, Wang-Chien Lee, and Zhen Lei. 2017. HIN2Vec: Explore Meta-paths in Heterogeneous Information Networks for Representation Learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management (CIKM '17). ACM, New York, NY, USA, 1797-1806. DOI: https://doi.org/10.1145/3132847.3132953 ↩

[6] Yuxiao Dong, Nitesh V. Chawla, and Ananthram Swami. 2017. metapath2vec: Scalable Representation Learning for Heterogeneous Networks. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '17). ACM, New York, NY, USA, 135-144. DOI: https://doi.org/10.1145/3097983.3098036 ↩

[7] Rana Hussein, Dingqi Yang, and Philippe Cudré-Mauroux. 2018. Are Meta-Paths Necessary?: Revisiting Heterogeneous Graph Embeddings. In Proceedings of the 27th ACM International Conference on Information and Knowledge Management (CIKM '18). ACM, New York, NY, USA, 437-446. DOI: https://doi.org/10.1145/3269206.3271777 ↩

SFFAI招募

现代科学技术高度社会化，在科学理论与技术方法上更加趋向综合与统一，为了满足人工智能不同领域研究者相互交流、彼此启发的需求，我们发起了SFFAI这个公益活动。SFFAI每周举行一期线下活动，邀请一线科研人员分享、讨论人工智能各个领域的前沿思想和最新成果，使专注于各个细分领域的研究者开拓视野、触类旁通。

SFFAI目前主要关注机器学习、计算机视觉、自然语言处理等各个人工智能垂直领域及交叉领域的前沿进展，将对线下讨论的内容进行线上传播，使后来者少踩坑，也为讲者塑造个人影响力。

SFFAI还将构建人工智能领域的知识树（AI Knowledge Tree），通过汇总各位参与者贡献的领域知识，沉淀线下分享的前沿精华，使AI Knowledge Tree枝繁叶茂，为人工智能社区做出贡献。

这项意义非凡的社区工作正在稳步向前，衷心期待和感谢您的支持与奉献！