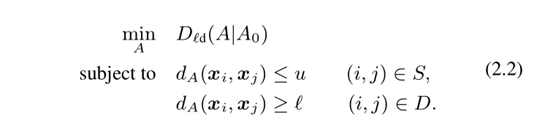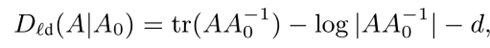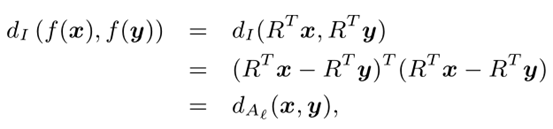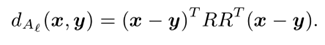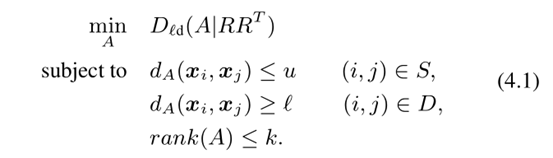博客 | 度量学习总结(二) | 如何使用度量学习处理 高维数据？

  本文原载于微信公众号：磐创AI（ID：xunixs），欢迎关注磐创AI微信公众号及AI研习社博客专栏。

作者 | Walker

编辑 | 安可

出品 | 磐创AI技术团队

【磐创AI导读】上篇文章，我们总结了一些常用于文本分类的度量学习方法，本文我们将探讨度量学习如何有效的处理高维数据问题。

Kmeans聚类、最近邻算法实质上都很依赖于底层距离函数，虽然通常实践上提倡现成的距离函数或手动调整的度量，但距离度量学习问题却寻求在半监督或完全监督的设置中自动优化距离函数。度量学习的目标是优化反映当前问题的领域特定概念的距离函数。

度量学习的算法会随着维数线性伸缩（高维数据），允许对学习度量进行有效的优化、存储和评估。它提供了基于对数行列式矩阵发散的框架，该框架能够有效地优化结构化的、低参数的马氏距离。

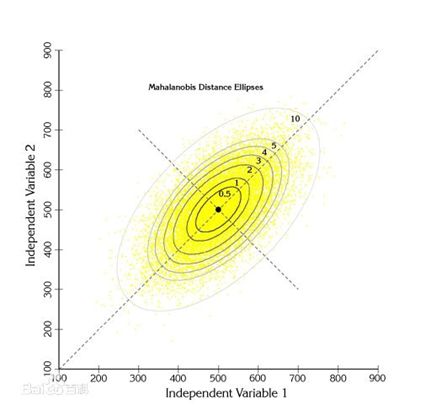
马氏距离是一类具有良好泛化性质的距离函数。马氏距离推广了k近邻分类器等算法常用的标准平方欧氏距离。直观地，马哈拉诺比斯距离通过缩放和旋转特征空间来工作，赋予某些特征更多的权重，同时结合特征之间的相关性。在数学上，该函数定义在由d×d正定矩阵参数化的d维向量空间上。

然而，在高维环境中，由于马氏距离函数与d×d矩阵的二次依赖性，学习和评估马氏距离函数的问题变得非常棘手。这种二次依赖性不仅影响训练和测试的运行时间，而且对估计二次参数的数量提出了巨大的挑战。

本文给出了结构马氏距离函数的学习算法。我们的方法不是搜索具有O(d 2)参数的完全d×d矩阵，而是搜索通常具有O(d)参数的压缩表示。这使得马哈拉诺比斯距离函数能够在高维环境中被有效地学习、存储和评估。

本文的技术贡献是计算两类结构化低参数矩阵的问题公式和结果算法：低秩表示和对角加低秩表示。低秩表示HDLR得到的距离度量与潜在语义分析（LSA）使用的距离度量类似。这个距离将数据投影到低维因子空间中，并且两个示例之间的结果距离是它们的投影之间的距离。我们的低阶方法可以看作是半监督的。LSA的变体是非常适合于需要更高召回的应用程序。第二种方法，HDILR，学习一个对角加低秩矩阵，并且非常适合于高查全率和高精度都很重要的问题。

在计算上，我们的算法是基于信息论度量学习方法。该问题被描述为学习满足给定约束集的“最大熵”马氏距离问题。在数学上，这导致了一个具有矩阵值目标函数的凸规划问题，称为对数行列式(LogDet)散度。我们提供了两种基于LogDet发散度的新算法，能够学习高维马氏距离。这两种算法都以O(d)的维数线性伸缩。

核心方法：使用LogDet框架来学习结构化半正定矩阵，并且类似于我们现在详细描述的ITML。该问题假设一组给定的相似性约束S和一组实例之间的不同性约束D。约束可以从真实标签推断(其中相同类中的示例被约束为相似，而来自不同类的示例被约束为不同)，或者可以显式地提供约束。

此外，ITML假设由正定矩阵A0参数化的基线马氏距离函数。正式目标是学习由A参数化的马哈拉诺比斯距离，该距离具有到给定基线矩阵A0的最小LogDet散度，同时满足给定约束：

LogDet目标函数D d(A|A0)是非负凸函数,当A=A0时,在没有约束的条件下最小化。定义在d×d正定矩阵A和A0上(其中|X|表示矩阵X的行列式)：

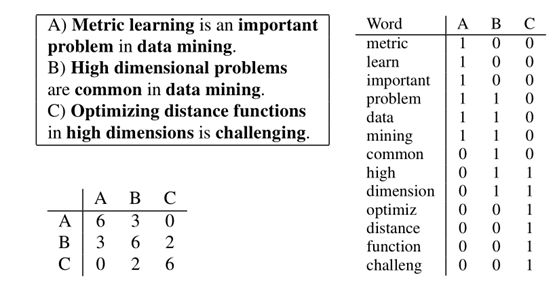
上边列出了三个句子。右边的表格显示了句子中每个单词的计数。从左下角的内积矩阵可以看出，即使这三个句子都是关于度量学习的，文档A和C之间的距离也很大。这个示例说明了当矩阵内积较大时，术语频率模型是相当精确的，但是当矩阵内积较小或为零时，术语频率模型可能不准确。

TFIDF是用余弦相似度来计算x和y的距离。但当x和y被标准化为具有单位L 2范数时，余弦相似性等价于标准欧氏距离：dl (x,y) = 2 −2∗cos(x,y)。在术语频率模型中，两个文档可以具有非常相似的上下文含义，但是可能不一定共享许多相同的单词。因此，两个文档之间的内积可能非常小，甚至为零，从而导致较大的欧几里德距离。因此，即使A和C在上下文上是相似的，模型也不反映它们的相似性。

本文中，我们提出了潜在因素模型，其根据对象的上下文或底层主题来表示对象来工作。潜在因子模型不是在原始的高维空间中表示对象x，而是提供将x转换为一些低k维空间的映射f。潜因子模型的目标是学习映射f，使得f(A)和f(C)彼此接近。

常用的一类潜在因素模型，如潜在语义分析（LSA）是由d×k投影矩阵R参数化的模型。函数可以表示为：f(x)=RTx。考虑两点x和y的潜在因素之间的欧氏距离：

其中：

低阶马氏距离也可以在O（dk）时间内有效地计算，因为二维实例x和y之间的距离可以通过首先通过计算R T x和R T y将它们映射到低维空间来计算，然后在低维点之间计算标准平方欧几里德距离b。

现在我们扩展全秩ITML算法来学习低秩矩阵。设R是秩k正则化矩阵A 0的d×k因子矩阵，即A0=RR T。我们将高维低秩（HDLR）度量学习问题表述为：

与用于累加的全秩ITML(2.2)相比，我们看到这里的A0是低秩的（A0=RRT），并且添加了额外的约束以强制执行最优马氏矩阵A的秩。考虑学习受矩阵线性约束的低秩核矩阵的相关问题，LogDet散度被推广到正半定锥，并且证明了两个矩阵是有限的。

现在我们提出算法1来解决我们的HDLR公式。该算法优化了问题（4.1）的稍微修改版本，该版本结合了松弛变量，以便在不正确或噪声约束的情况下允许违反约束。松弛惩罚参数γ确定给予目标的LogDet分量与目标的松弛惩罚分量的相对权重。当γ较大时，对松弛项赋予更多的权重，最终的解将更接近于满足约束条件。当γ较小时，更注重LogDet目标，产生更接近正则化矩阵A 0的平滑解。在实践中，通过交叉验证来选择γ。

该算法采用循环投影的方法，通过迭代地将当前解投影到单个约束上。该算法不是直接处理d×d矩阵A，而是优化其d×k因子矩阵B。在实践中，可以通过监视对偶变量λ的变化。步骤5-10计算投影参数β。在步骤11中，该参数然后用于通过秩1更新来更新B。每个投影都可以以闭合形式计算，并且需要O(dk)计算，其中k是A0的秩。

最后，最优解是A=BB T。注意，后一步可能不需要，因为如下所示，可以在O(dk)时间内计算两点之间的低阶马氏距离，而无需显式计算A。

【总结】：本文介绍了度量学习如何处理高维数据问题。欢迎大家持续关注我们的公众号，学习更多机器学习知识。

欢迎扫码关注磐创AI微信公众号：

点击阅读原文，查看更多内容↙