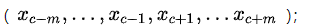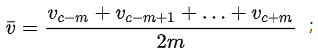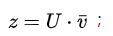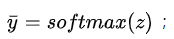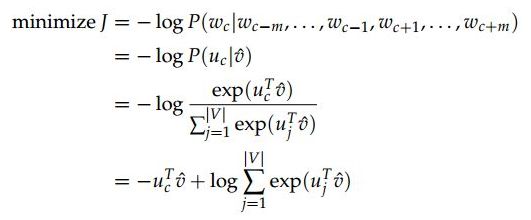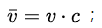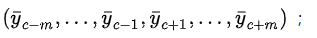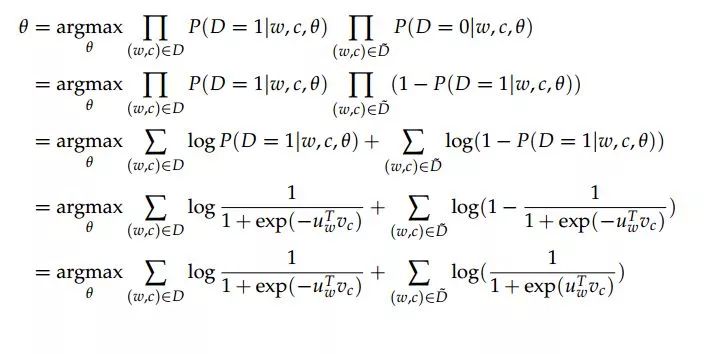博客 | 斯坦福大学—自然语言处理中的深度学习（CS 224D notes-1）

本文原载于邹佳敏知乎专栏“AI的怎怎，歪歪不喜欢”

关键词：自然语言处理，词向量，奇异值分解，Skip-gram模型，CBOW模型，负采样。

本文从NLP的概念出发，简述当今NLP所面临的问题，接着讨论使用数值向量的词表达，最后介绍几种词向量的常用表达方式。

一， NLP简介：

NLP的目的是通过设计算法的方式让计算机理解人类的自然语言，从而帮助人类完成指定的任务。任务通常有以下几类：

简单任务：拼写检查，关键词索引，查找同义词；

中等任务：解析网站或文档信息；

困难任务：机器翻译，语义分析，指代歧义，机器问答。

在面对不同任务时，首先也是最重要的一点：如何将词语表述成模型可接受的输入，如何计算词语间的相似程度等。词向量，很好的解决了上述问题。

二， 词向量：

英语中有1300万单词，大部分单词间都存在联系，比如，酒店和旅馆。因此，我们想将单词编码至一个向量，以至于它们可以用“词空间”内的点来表示。最直观方案，存在一个N维空间（N<<1300万），它能够表示单词的所有语义维度，则空间中的每一维代表单词在某一方面的语义。比如，构建一个3维空间（时间，阶层，性别），则国王（现在，顶级，男性），王后（现在，顶级，女性），太子（未来，顶级，男性）就可以分别用这个3维空间来表示。

为了方便理解，我们先从最简单的one-hot向量开始。one-hot将有序排列的全部单词看作整个向量空间，向量内只有0，1两种数值，如果某个单词出现在第i个位置，则向量的第i个元素是1，其他元素是0。one-hot解决了单词的表示问题，但却不能拿来计算单词间的相似度，因为，任意两个词向量间都是正交的，即内积为0，模1，相似度同样为0。

aardvark，a，at，...，zebra在语料库的one-hot表示

因此，我们需要降维词空间，尝试去找一个可以计算单词间相似度的子空间。

三， 基于SVD的方案

该类方案通常需要先遍历整个语料集，找到所有词的共现矩阵X，再对X做奇异值分解得到 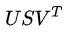 。最终，U的行空间向量即为语料词库的词向量。那么，问题来了，X应该怎么选？

1， 词-文档矩阵：相似的词会在相同的文档中经常出现。

按文档粒度遍历语料库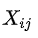，  表示单词i出现在第j篇文档中的次数。显然X的维数是V*M，V表示词汇量，M表述文档数。这样的X不仅巨大，还会随着文档数的增加而暴增。因此，该方案是不能承受的。

2， 共现窗口矩阵：相似的词会经常一起出现。

将语料集看成整体，在一个指定大小的上下文语境窗口内，记录每个单词出现的次数。显然，X的维数是V*V，V表示词汇量。举例说明，假设语料集内有3句话：

语料库的size=3的共现窗口矩阵

对X使用SVD，得到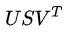 ，选择特征值矩阵S的前k大个特征值降维，则U对应的子矩阵就是我们需要的词向量矩阵，它是V*k维，即词典中的每个词用k维向量近似表示。

SVD后降维整个词向量空间

3， 问题和解决方案：以上2种方法得到的词向量，对语法和句法都有较好的表示。但仍存在以下5个问题和3个解决方案：

3.1.1， 矩阵X会随新词的加入或语料大小的改变而经常变化；

3.1.2， 因为大多数单词并不会经常共现，矩阵X会很稀疏；

3.1.3， 矩阵X维度极大，通常是  ；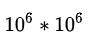

3.1.4，  的训练时间复杂度（SVD算法）；

3.1.5， 矩阵X需要预处理以应对词频间的极度不平衡。

----------------------------------------------------------

3.2.1，忽略停用词；

3.2.2，采用加权距离窗口，即基于文档中单词的距离加权共现词频；

3.2.3，使用相关系数，同时用负数替换词频0的位置。

四， 基于迭代的方案：

对上述问题，更优雅的解决方案

与存储并计算全量语料集信息不同，我们通过构建模型的方式，不断迭代，最终在给定的上下文环境中编码词的概率。

假设存在一个概率模型，它有已知参数和未知参数，每使用一个训练样本，评估并最小化模型损失，就能朝未知参数的真实估计更近一步，最终输出由已知参数和估计参数构成的模型。

1， 语言模型：Unigram，Bigram等

首先尝试计算一句话出现的概率：”the cat jumped over the puddle”，因为它完整的语法，句法和语义，优秀的语言模型会得到一个极高的概率。相反，”stock boil fish is toy“，不符常识，毫无意义，计算的概率就很低。

该模型的数学化表达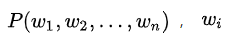：  代表第i个单词。如果每个单词都是独立出现，和它的上下文无关，则  ，这就是最简单的Unigram模型。显而易见，Unigram并没有考虑任何合理且有关联的上下文信息，更重要的是，完全错误的句子可能会被计算出极高的概率。

因此，进一步地，假定一个单词和它前面一个单词相关，该模型就变为 ，我们称它为Bigram模型，看上去很朴素，但在实践中非常好用。另外，窗口大小为1的共现窗口矩阵，可以达到相同的目的，但它需要存储和计算全量语料集。

2， 连续词袋模型（CBOW）：根据指定窗口的上下文预测或生成它的中心词。

比如，根据{“the”,“cat”,“over”,“the”,“puddle”}预测或生成单词jumped。

首先，模型已知的参数，我们用one-hot向量表示整个上下文，记为  。同时，因为CBOW模型仅预测一个单词，所以输出是一个中心词的one-hot表示，记为   。

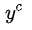
接着，模型未知的参数，我们定义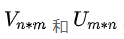矩阵，其中n是用户指定的词向量空间大小。V是输入的词矩阵，即V的第i列表示单词  的n维词向量，记为列向量  。同样，U是输出的词矩阵，即U的第j行表示单词  的n维词向量，记为行向量  。

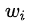
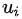
所以，CBOW模型，本质上就是学习每个单词  的输入矩阵列向量  和输出矩阵行向量。详细而言，有以下6步：

2.1，生成以one-hot向量表示，size=m的上下文窗口输入：

2.2，初始化矩阵V，生成模型的输入词向量 ：

2.3，计算上下文窗口内词向量的均值向量：

2.4，初始化矩阵U，生成得分向量

2.5，使用softmax将得分向量z转换为概率

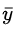
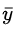
2.6，真实的y是中心词的one-hot向量，而  是对它的预测。因此想办法找到最适合的V和U，使y和  尽可能接近，就可以达到目的。为了实现上述目标，首先需要定义目标函数。

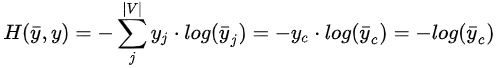
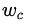
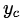
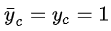
通常，概率领域的建模会使用信息理论来测量2个分布之间的距离。在CBOW模型中，我们选择交叉熵作为损失函数，即  ，y是one-hot向量，中心词  所在的位置c，值  是1，其余为0。显然，当 时，损失H最小为0，但当  时，损失H约为4.6。因此，交叉熵H给概率分布的距离计算提供了一个非常好的方法。

最优化目标函数：

CBOW的目标函数

最后，我们使用梯度下降迭代更新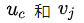， 收敛到最终词向量。

3， Skip-Gram模型：根据中心词，预测或生成它的上下文单词。

比如，根据jumped，预测或生成{“the”,“cat”,“over”,“the”,“puddle”}。

显然，交换CBOW模型的x和y，Skip-Gram模型的输入是中心词的one-hot向量x，定义输出为  。词向量矩阵V和U和CBOW模型相同。它的模型训练同样有以下6步：

3.1，生成以one-hot向量表示，中心词c的词向量x；

3.2，初始化矩阵V，生成模型的输入词向量

3.3，因为输入只有1个中心词，无需均值化，

3.4，初始化矩阵U，类比 ，生成2m个得分向量 :

3.5，使用softmax将每个得分向量都转换为概率：

3.6，最小化softmax概率和真实 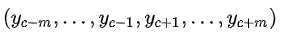 间的损失函数；

值得注意的是，Skip-Gram的目标函数需要建立在朴素贝叶斯的条件概率独立的假设上，即，除了中心词，所有的上下文词都相互独立。

Skip-Gram的目标函数

4， 负采样

上述损失函数的|V|极大，任何一步的迭代和更新都会花费O(|V|)时间，一个直观的优化，就是去近似迭代它。

对每一次迭代，我们并不会遍历整个词库，而只是选取几个反例而已。具体而言，我们从一个噪音分布 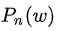 中随机选择反例样本，其概率通常设定为语料库各词频的3/4次幂，我们将它称作负采样。假设，is在语料库的词频是0.9，Constitution是0.09，bombastic是0.01，其各自的3/4次幂分别是0.92，0.16和0.032。因此，使用3/4次幂负采样到bombastic的概率相比之前增大3倍。即，相对而言，低频词更容易被采样到。

基于负采样的Skip-Gram模型的优化目标和常规Skip-Gram不同。考虑一对中心词和上下文(w,c)，P(D=1|w,c)表示(w,c)出自训练语料集的概率，P(D=0|w,c)则表示(w,c)不在训练语料集中的概率。因此，我们的目标函数就变成，当(w,c)确实在语料集中时，最大化P(D=1|w,c)，但当(w,c)不在语料中时，最大化P(D=0|w,c)即可。在这种场景下我们选用最大似然函数的求解目标函数。

我们使用sigmoid函数对P(D=1|w,c)建模，即， 是模型未知参数的同时，也是我们前文提到的V和U。定义，  表示“错误”或“负”的语料组合，比如“stock boil fish is toy”等，它是按P_n(w)采样出的K个错误表达。因此，具体的目标函数如下：

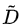
基于负采样的Skip-Gram目标函数