数学建模研究过程指导(精编版) Part II

挖掘情境中数学模式的两种方法
研究方法指导 03
当我们分析了问题,也获取了数据之后,面对的就是如何去挖掘其数学模式。比较常用的方式有两种——数据挖掘方法和机理建模方法。这两种方法可以有效地帮助我们将课题中的各种现实约束和关联转化为清晰、简洁、方便处理的数学语言
方法1:数据挖掘方法。
所谓的数据挖掘方法,顾名思义,就是从数据入手去挖掘数学模式。这种方法往往适用于数据繁杂且机理不清的课题情境。下面我用一个实践案例来简述其步骤。下表为齐云山摩崖石刻文物保护项目工程的现实数据。石刻文物保护界并不知道这些项目之间的定量关系。
表1 齐云山摩崖石刻文物保护项目工程的现实数据。
下表2 新鲜岩石数据。:

用表1中各点位的数据除以表2中的数据,这被称为标准化处理,为了消除量纲的影响,突出表1中的文物检测数据和新鲜岩石数据的相对值。标准化处理后得到如下的表3(见下页)。
表3中对于每个检测指标有前后两列:一列是状态量,为前后两次检测的均值;一列是变化量,为前后两次检测的差值。它们都取的标准化之后的结果。为了扩展观察,还可以加入其他的一些列,例如表3中的后10列,就是对标准化数据取对数后的数值在前后两次检测时的均值(作为对数状态量),及前后两次检测数值的对数值的改变量。
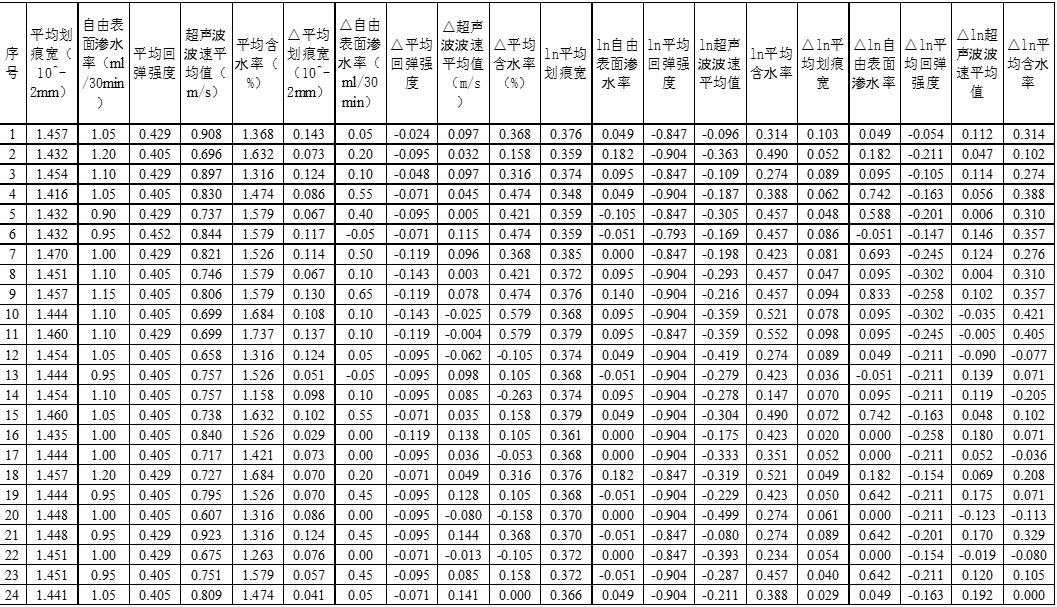
表3 标准化后的数据。
上述操作均可在EXCEL中利用EXCEL的内建公式批量处理完成。
在得到表3之后,就可以着手开始数据挖掘工作了。比如我们将自由表面渗水率(表3第3列)及其变化量(表3第8列)分别作为横坐标和纵坐标,可以描绘出下图1所示的散点图。
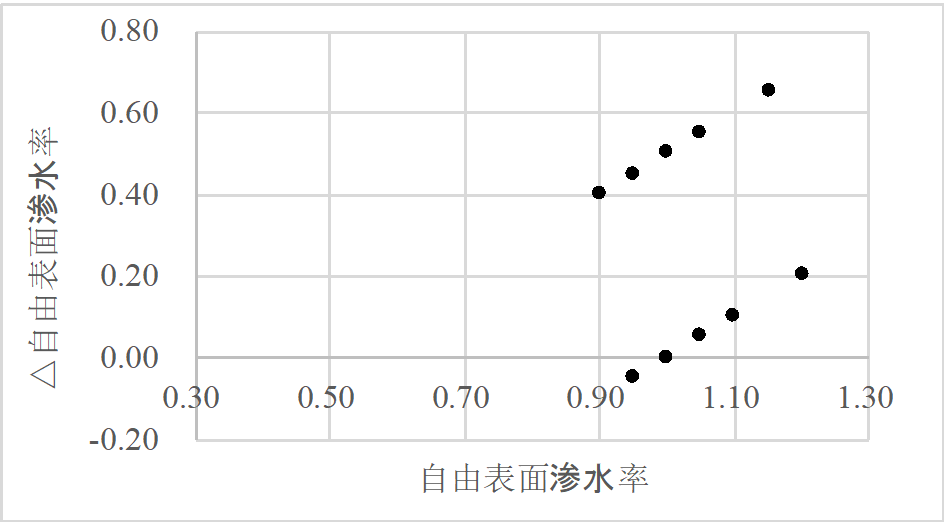
从图1可以非常清晰地看到这些数据点分布在两条直线左右,分为两类。实际上,再通过实地考察可以看到这两类点分别位于齐云山的“向阳面”和“背光面”,如下图2所示。


图2 齐云山摩崖石刻的阳面和阴面。
对这两类三点图分别用EXCEL添加趋势线,就可挖掘出如下的数学方程,其中代表自由表面渗水率。
对于第1类点有,对于第二类点有
。
其实还可以通过类似的方法得出更多的方程,这里主要是为了说明方法,就不赘述了。
方法2:机理建模方法。
有时候课题的物理极值比较清晰,并且有一定的物理、化学、生物等学科的学科经验支撑,这个时候就可以在代入数据前,先进行机理的建模,得到待定系数的方程,然后再利用数据拟合这些待定系数的最优取值,从而得到最复合实际情况的数学模式。
依然以一个简单的案例为例来讲解这种方法:
假设现有一种初发的流行疾病,如果我们能够基于目前掌握的情况对它未来的传播规律有一定的了解,那么显然有助于疫情的控制。下面我们将建立一个数学模型去解决这个问题:首先将人群分为三类,分别是“易感染但未感染者”(用函数S(t)来表示,单位:人;t ≥0 代表时间,单位:周,下同)、“已感染,但未痊愈或死亡者”(用函数I(t)表示)、“已痊愈或已死亡者” (用函数R(t)表示)。假设这种疾病一旦已感染过一次之后不会再度感染。下表4中为以一千人为样本容量前10周的疫情跟踪统计情况。简便起见这里不考虑病毒的变异。
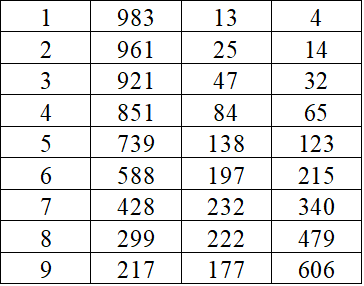
表4 前10周千人样本的疫情跟踪统计情况,数据采集时间为每周一。
因为人口数量的最小单位为1,而样本容量为1000,所以不妨设S(t)、I(t)、R(t)均为关于时间的连续可导函数。关于疾病传播的两个常识性认知是:
(1)“易感染但未感染者”的人数S(t)在逐渐减少。S(t)越大,S(t)下降越快;“已感染但未痊愈或死亡者”人数I(t)越大,S(t)下降越快。而且S(t)越大,I(t)对S(t)下降速度的影响越明显。
(2)“已痊愈或已死亡者”的人数R(t)的变化速度和I(t)正相关。
根据(1),S'(t)和S(t)I(t)乘积负相关,R'(t)和I(t)正相关,于是有
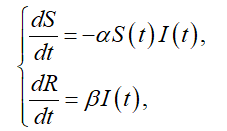
其中 α >0, β >0 分别为待定的正比例常数。
如果再假设总人口数不变,则为定值,即存在正常数 C 使得
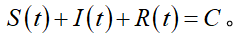
对上式两边求关于时间的导数,可得
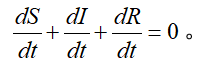
于是得到微分方程组
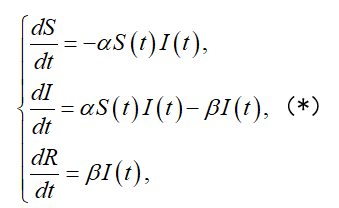
上面就是利用机理建模找到的含有待定参数的数学模式,再利用表4中的数据,利用EXCEL的添加趋势线功能就可以得到参数的最优取值。具体地说,需要先将表4拓展为下面的表5。
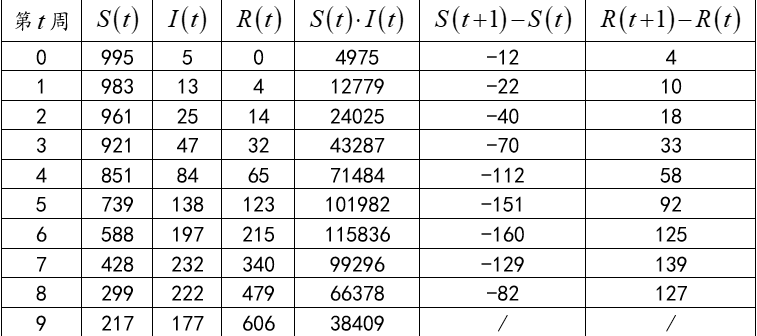
表5 为估计参数 α, β 对表4所做的扩展。
用EXCEL可以针对所需的某两列,描绘出如下的散点图及趋势线,见图3。
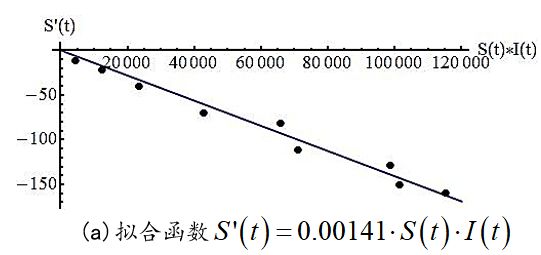
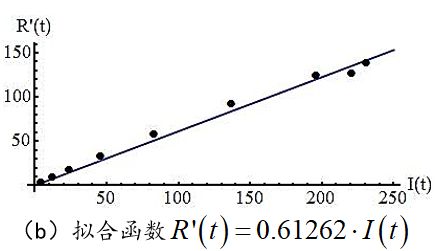
图3 对参数的拟合效果。
进而得到参数确定后的数学模型
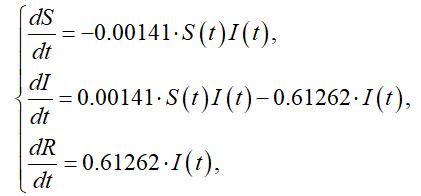
利用这个模型就可以进一步分析很多事情,例如:预测何时疫情发展最快?何时正患病人数达到最多?当我们有了合适的预测,就可以进一步去建立一些对应的应对措施,例如:何时投放药物?如何平衡药物的研发时间(减少毒性,增强药效)和投放时间之间的平衡(越早投放能获得治疗的人越多,但是药物毒性副作用也就越大)。这里只是为了说明方法,不再赘述。
连续模型的使用范围、建立和求解方法
研究方法指导 04
1.连续模型的使用范围。
昨天我们介绍了挖掘情境中数学模式的两种方法,有的同学可能会产生疑惑:为什么昨天文中所建立的模型都是微分方程呢?(注:所谓微分方程,就是含有函数的导函数及原函数的方程,其未知数并非是数,而是函数,借由微分方程我们可以求出复合条件的函数)回顾一下昨天文中的模型(只看方程),它们是:
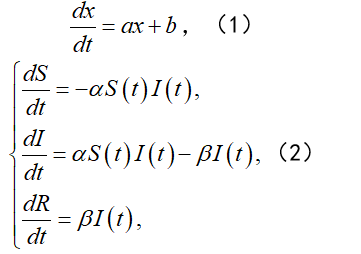
首先,需要强调:并非所有的课题都适合建立微分方程模型,这并不是万能的方法。建立微分方程模型的前提有三个
1).微分方程中所求的函数需要可求导数;
2).微分方程中所求的函数需要是连续的;
3).是状态量的变化影响着变化速率。
已经高二并学过高中教材内的导数章节的同学一定知道:满足1)的函数肯定满足条件2),但是满足条件2)的却不一定满足条件1)。
如果你能稍微回顾一下昨天文中列举的课题,就会发现上面两个方程(1)和(2)分别关于“石刻文物的含税量随时间变化的函数”以及“疫情发展过程中三类人群数量变化”。对于前者,自然可以视为一个光滑的自然过程,抛去一些偶然的间断点,整个函数肯定是可导的。而对于后者,虽然人数的取值是在正整数集当中,不可能从1人变为1.5人,看起来不连续。但是由于样本基数很大(样本容量1000人,统计全体是全市人口),所以每次1人的变化相对总量可以视为无穷小量。同时,正如现实中没有两片同样的叶子,如果充分精确的观察地话,每个人患病的时间点不可能重合(若重合,只需要提高时间的精度即可,例如:甲和乙患病可能都是在第1天第1小时,但是提高时间精度后可能就会观察到甲在第1小时第5分钟患病,而乙在第1小时第10分钟患病,如果不行就继续提高时间精度即可)。这就是说,对于传染病课题来说,三类人数在时间精度充分高的清华下,都是以1人为单位及样本总量的0.001倍进行变化,于是近似认为这个过程是个连续过程,是合理的假设。
此时有的同学可能还会有疑问:按照你的说法,假设连续是挺合理的,但是为什么我们还能假设可导呢?要知道连续不一定可导啊?
如果同学们对单变量微积分再多一些了解,就会发现一个熟知的结果:“可导函数在连续函数中是稠密分布的”。这个说法不是很严格,但是直观地说,就是任何连续函数经过幅度充分小、不超过误差允许的范围的微扰之后,肯定能变为一个可导函数。这就和任何无理数的任何充分小的周围都存在有理数一样。这一点我在十一学校的数学建模课上作为重点推导论证过,这里因篇幅就不再赘述了,感兴趣的同学可以查阅一些微分拓扑的入门文献,一般在其第一章就会提到这个经典结果。
2.连续模型的建立方法。
通过了上面的论述,大家就会了解:自然界中很多过程都可以用连续模型来描述。但是这个连续模型往往并非是直接给出的,需要我们去探索。而微分方程,就为寻找——或者用数学的语言来说——求取这些函数(也就是自然界的深刻规律)提供了非常好的支撑。
正如微分方程的定义中所指出的那样,为了建立微分方程(组),你需要建立关联函数状态量和变化量的方程。在昨天的短文中,我给出了两种建立这类方程的两种途径——数据挖掘法和机理建模法。今天就不再重复了,同学们可参看昨天发布的内容。
3.连续模型的求解方法。
下面以方程(1)为例,利用高中课内知识,介绍3种常用解法。
方法1:直接求解析解。
对于一些简单的微分方程,高中所学的数学足以让我们准确地求出其解析解。例如方程(1):
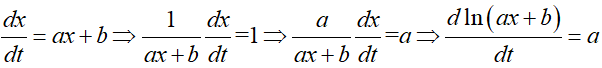
于是 ln(ax+b) 一定是关于时间 t 的线性函数,于是可得
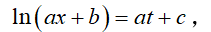
其中 c∈R 为某个待定系数,可以通过数据拟合得到。进一步化简可得
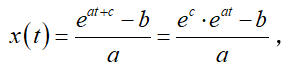
将 t=0 代入上式,可得,即
,进而可得
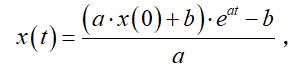
其中为时函数的取值,即其初始值。
方法2:定性分析法。
绝大多数的微分方程,即使是一阶微分方程,也是无法、或者很难像上面这样解出解析解的。假设刚才的方程(1)我们不会解,还能对其进行分析吗?答案是肯定的,这也是微分方程的威力所在,你可以仅仅根据方程本身,来观察出很多关于其解——函数——的一些蛛丝马迹。


方法3:数值估算法。
上述的定性分析法能观察出所求函数的部分趋势,但是可惜的是没法定量预测。而定量预测往往是工程和科学中的必要需求。当然如果我们可以解出解析解,像方法1中的那样,一切自然迎刃而解。假设我们无法解出解析解,但是还想得到定量预测,该怎么办呢?
其实我们在高中就学习过相关的方法,那就是数列!
首先,我们将微分方程离散化:

当然,如果不幸遇到一个更为复杂的递推关系,使得其数列通项很难求出,我们也可以通过递推关系和首项来逐项计算(利用EXCEL,即使逐项递推计算几十万步,也可在瞬间完成。)
上述方法被称为欧拉近似法,是微分方程数值分析的常用方法。其几何原理如图1所示。
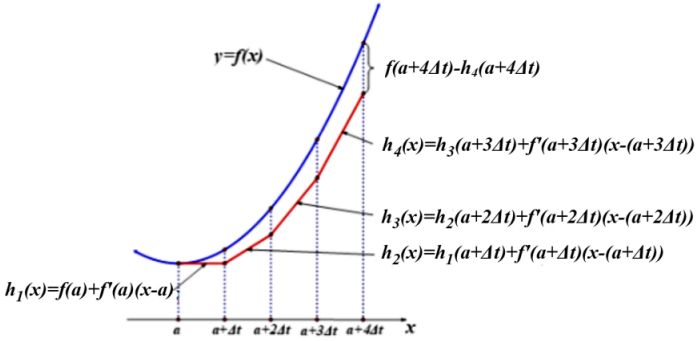
图1 欧拉近似法原理图示。
备注1:这种方法是对连续模型的离散化,所以预测值也只能是一些离散的点,而这些离散点的间隙是无法预测的。好在当函数 x(t) 充分光滑时,如果离散的点取的足够多,间隙处的函数值不会偏差很多。
备注2:方法3只是一种估计的方法,结果不是 x(t) 的真实值,但是考虑到 x(t) 本身也就是对自然界现象的估计,所以是否是真实值问题并不大,关键在于近似的精度是否足够高。可以证明,当所求函数 x(t) 的导数有界时,这种方法可以任意经典逼近所求函数 x(t) 的真实值——步长△t>0 越小,则精度越高。但 △t 是越小,计算的复杂度就越高。例如:当步长为 0.0001 时,要预测 x(1),如果利用递推式逐项计算,就需要计算100000步,虽然精度高,但是计算代价也大;而步长为 0.1 时,要预测 x(1),同样的方法只需计算 10 步即可,但是这样一来精度就会下降。所以如何寻求计算代价和精度之间的平衡,有时需要反复尝试,这是一种权衡的艺术。
从连续模型到离散模型&离散模型的常见类型及其研究方法
研究方法指导 05
1.先总结一下两天讲的重点——连续模型。
前两天的重点都在于连续模型的讨论,这里先总结一下。连续模型可以分为两大类——最优化模型和方程模型,它们的基本形式如图1所示。连续模型的本质是观察一种几何(可能是高维空间中的几何)模式,最优化模型是寻求某个几何对象沿着某个方向的“顶点”,方程模型则是寻求某个何对象上复合某种条件的截面(截线)。
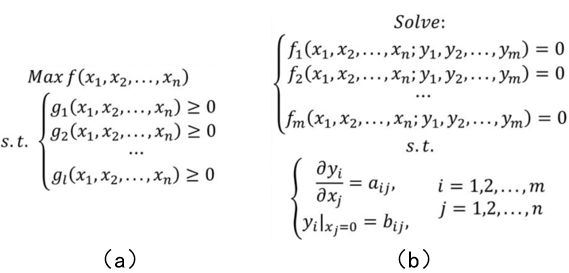
图1 连续模型的两类:
(a)最优化模型;(b)方程模型。
这里需要指出两点:
(1)最优化模型和方程模型并非是割裂开的,正相反,当我们为最优化模型寻找目标函数或约束条件中的诸多函数时,往往是通过方程模型来实现的;同时当我们想确定方程模型中方程的参数取值时,又往往是通过最优化模型来实现的;有时这种互相帮助的过程甚至要累加很多层,甚至是迭代到无穷多层。所以千万不要把它们从认识上割裂开。
(2)虽然无论是最优化模型还是方程模型,在图1中的展现形式都很简洁,但是在确定各个函数、方程参数的过程中,会有很多的本质难点展现,这在很多时候都是比较困难甚至难以解决的问题。所以不要被它们最终的简洁性所蒙蔽。好的数学模型确实是简洁的,但是为了建立这些模型所需要的数学功底和数学上的努力,甚至是数学之外的交叉学科的努力,都是庞大、精细而必要的。
2. 离散模型的常见类型及其研究方法。
所谓离散,从数学上来看有这样几层含义:孤立的、局部有限的、不连续的、间断的、可列的。人类对于离散的认知有时建立在对连续的认知的基础上(例如股票价格走势),有时也并非如此(例如魔方或者拼字游戏)。
离散模型很难像连续模型那样给出最终的统一形式,但是不见得不能大致分类。数学可以综合依据处理风格、问题来源和解决方法,将常见的离散模型分为如下三类:
第1类:连续模型的离散截影。
第2类:离散状态的概率转移。
第3类:基于代数结构的对称分解。
下面我们分别来谈一谈这三类模型及其研究方法。
2.1 第1类:连续模型的离散截影。
所谓的连续模型的离散截影,其实就是在图1中两类连续模型的基础上添加一些离散的要求,例如函数的取值只能是0或1、自变量取值必须是正整数等。在添加了离散要求后,往往会将原来的连续问题变得更加难以解决。这从数学上来看似乎很容易理解,因为条件增加了,而且增加的条件并非致力于将原本的问题简化,而是添加了新的需求。但是如果想把这种“难度的增加”理解地更为透彻,就需要用几何的视角。
实际上,正如本文第1部分所说的,两类连续模型本质上都是将问题转化为几何对象来研究,连续的几何对象提供人们很多的直观想象的可能。但是如果问题只限制在连续几何对象上的一些离散的点上,那么很多直观想象就将变得不再直观。一个最典型的例子就是:当我们求数列极值时,我们不可以将其求导,即使对数列通项公式所对应的可导函数进行求导,也往往无法直接求出数列的极值,还需要进一步的比较,这还仅仅只是最初等的情形,复杂的、高维的情形将更难以想象。
但是毕竟这类离散模型来源于连续模型,借用连续模型的几何观,和计算机强大的运算和搜索能力,我们可以通过如下的方法来讲问题逐步解决,这也是工业上的常用办法:
Step1:首先对离散模型松弛化,即仅仅观察其对应的连续模型,而先不考虑离散条件。
Step2:求出该连续模型的最优解。
Step3:考虑离散条件,在上一步获得的最优解附近进行搜索(这时可以是暴力搜索,也可以是梯度搜索或牛顿法搜索),搜索结束后,如果寻找到离散模型的最优解,则问题解决;如果没有找到离散模型的最优解,则利用切割空间的办法,将这个“附近”从可行区域中“切除”。
上面的这种方法被称为“切割空间法”。
可能有的同学之前看过一些科普书籍,听说过“三角剖分”、“单纯形法”、“有限元方法”等方法,虽然从名字上可能会让人想入非非,但是这些方法是为了寻找难解的连续模型的近似数值解,一般来说并不能改造为离散模型的解法。学习时要明确这一点。
2.2 第2类:离散状态的概率转移。
有时我们研究的问题有这样的属性:研究对象按照一定的概率随机地在几个有限的状态之间来回跳转。例如:中午吃饭去哪个窗口?晚上买菜家门口哪家超市?日常生活中我们根据喜好会有概率的偏爱,这一家去得多一些,那一家去得少一些,但是一个地方去多了还是想换一换心情,所以其它地方也会光顾。对这些问题进行数学建模时,第2类离散模型就是非常适合的选择——即,离散状态的概率转移模型。
对这类模型来说,一个最重要的目的就是要找到长期以往到达各个状态的可能性地大小,从而给出状态转移落脚点的统计意义上的分布规律。这对于商家也好,或者就是对于我们自己来说,都是非常有意义的观察。那么如何来做这件事呢?
我举一个简单的例子,小明每天要么吃苹果,要么吃梨。假设他前一天吃了苹果,那么后一天吃苹果的概率就是1/2,吃梨子的概率也是1/2;如果他前一天吃了梨子,后一天吃苹果的概率就是2/3,吃梨子的概率变为1/3。问长久以往,小明大约有百分之多少的天数在吃苹果?有百分之多少的天数再吃梨子?其状态转移可以用如下表1中的列表来呈现。
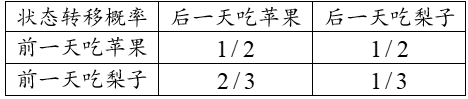
表1 小明吃苹果和梨子的转移概率。
假设小明第一天吃苹果的概率为 p,吃梨子的概率为 1-p。利用高中所学的概率中的加法原理和乘法原理,我们很容易计算:

如果是有耐心的同学,利用所学的数列递推的知识,或者直接利用EXCEL表进行多次计算,可以发现,当天数非常大时,小明吃苹果的概率趋于一个和无关的定值(保留4位小数,具体的计算留给同学们自己尝试,会矩阵运算的同学借助矩阵的形式计算更为简便,但是没有本质区别)。
于是我们就得到了结论:小明大约有的日子吃苹果,有大约的日子吃梨。
这种概率被称为“极限概率”,它是一种统计观察。有时还会出现极限概率不存在的情况,或者极限概率呈周期性循环的情况。上述研究方法是离散马尔可夫链的一种初等形式,再深入的讨论属于离散过程的分支范畴,不再赘述。同学们遇到此类问题只需要具体问题具体计算和分析即可。
2.3 第3类:基于代数结构的对称分解。
有时,离散模型还来自于对对称性的观察和研究。这类问题中最典型的就是魔方问题。关于魔方问题顾险峰(丘成桐先生的学生,和丘先生在上个实际90年代合作创理“计算共形几何学”,蓬勃发展至今)曾经写过上、下两篇非常优秀的博客文章,我将其链接放在这里:
第1篇:
mp.weixin.qq.com/s/ndwhTiHlDwOSlyI375kCmA
第2篇:
mp.weixin.qq.com/s/ndwhTiHlDwOSlyI375kCmA
具体的分析顾老师写得很清楚,这里不再赘述。但是我还是想举出几点需要注意的地方:
(1)基于代数结构并不意味着抛弃其几何结构。实际上,在上个世纪数学家们的一个共同的努力方向就是将代数结构和几何结构统一起来,这激发创立了很多目前非常核心的数学分支,例如:代数几何、不变量理论、曲面变换群理论、模形式理论等等。大家耳熟能详的数学家,例如希尔伯特、庞加莱、陈省身、格罗滕迪克、韦伊、塞尔、丘成桐等等都做出过非常伟大(本质而且影响深远)的工作。
(2)如果你想将你的模型建立成这种类型,那么建议你至少事先补充一些群论的基本知识、方法和结论。否则很容易浮于表面,难有深入的发现。
(3)即使你具备了一些群论、环论的知识技能,也千万要将这些理论结合具体的例子来理解。这是一个非常实用且关乎一生的忠告——千万不要在概念里做游戏。数学从某种角度上来说是关于例子的学科。我们拿现在很火爆的量子信息学举例来说,里面有一个非常基本的概念叫“正规算子”,如果你能够证明关于正规算子的普分解定理,这当然很好而且必要,但是你却写不出几种不同类型的具体的正规算子,当别人给你一个具体的正规算子也不会计算出其普分解,那么实际上你对正规算子实际上依然一无所知。“不要在概念里做游戏”,这是我的北大导师、国际知名代数曲面专家蔡金星老师在我迷茫时给我的忠告,我一直受用至今,这里我也分享给各位同学!