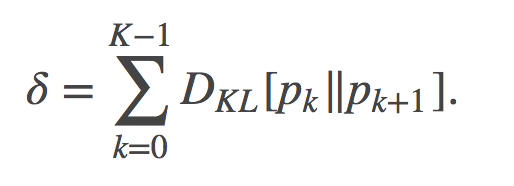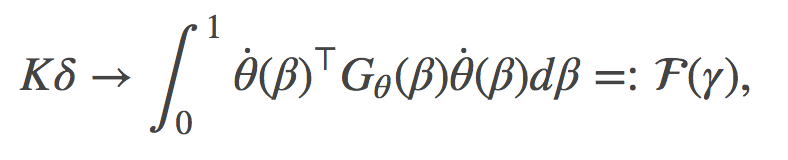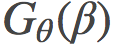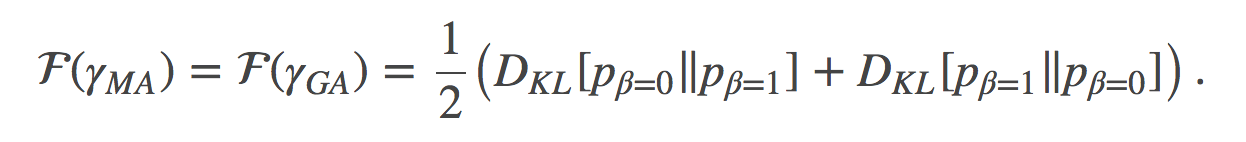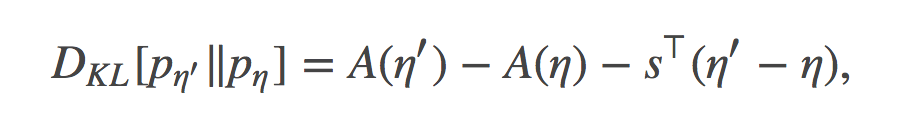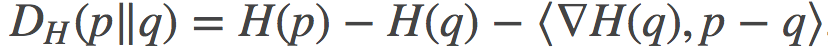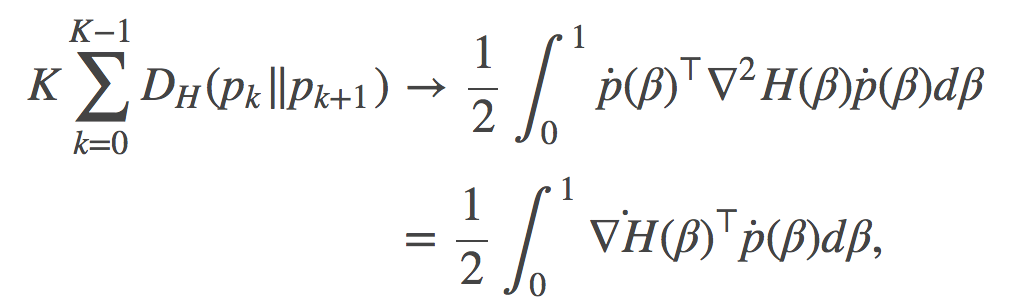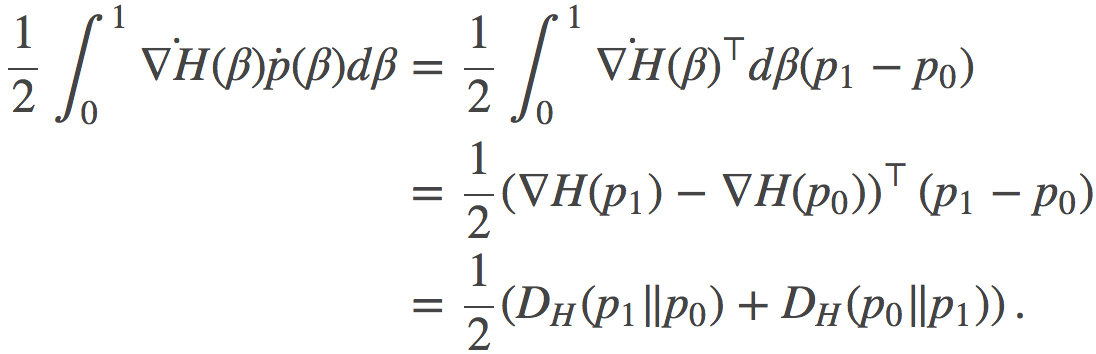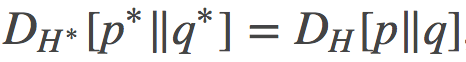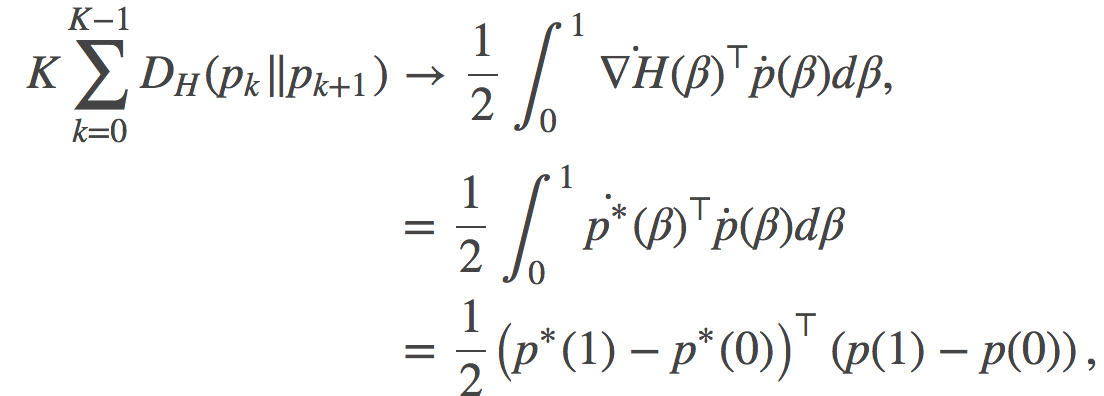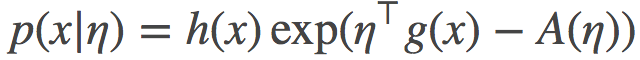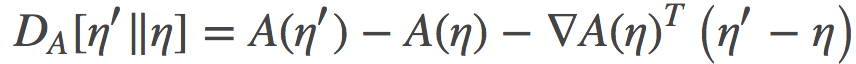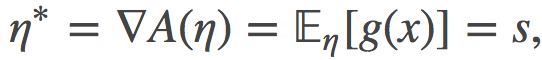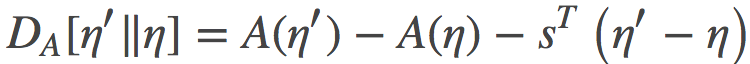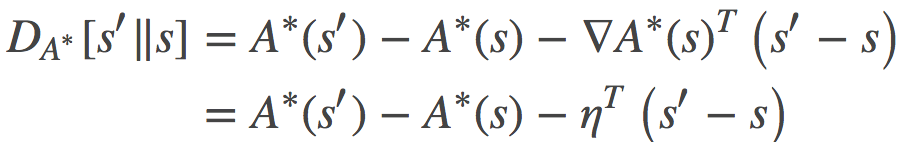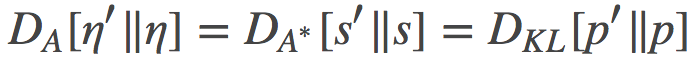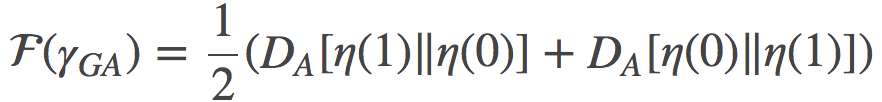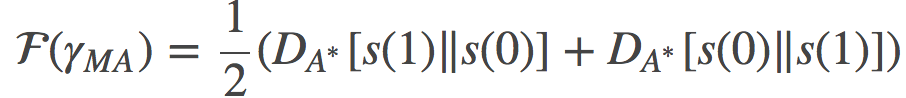不服来战！多伦多大学教授500美元挑战整个机器学习圈子

翻译 | 王赫

编辑 | Donna

【AI科技大本营导读】Hinton大神CSC321课程的“接班人”，加拿大多伦多大学副教授http://www.cs.toronto.edu/~rgrosse/Roger Grosse在Twitter上公布了一项悬赏金额500刀的挑战，为了找出一个能证明他在moment averaging中所提出的定理2的“世外高人”：

“在我的讨论关于moment averaging文章中, 文中的定理2让我颇为感到意外, 可以说是在整个机器学习领域里都让我感到最难以捉摸不透的数学结论之一。它的证明虽然很短, 但我依旧很难直接地把握到其中的精髓, 也不知道它为什么是正确的。如果有人能对此给出既清晰而又发人深省的解析, 我愿为此付500刀悬赏!”

— Roger Grosse (@RogerGrosse) 2017年11月27日

Twitter的机器学习研究员Ferenc Huszár则对此作出回应，他在博客inFERENCe中这样写道：

为了回答这个问题，我这个帖子可能阐述的会让你感到略显模糊。而且，若我们不在退火重要性采样(annealed importance sampling)的背景下讨论的话, 这可能压根就没太大意义。不过, 在写这个帖子的过程中，的确让我有机会好好聊一聊关于Bregman散度和指数分布族(Exponential Families)中一些很有趣的内容， 希望能借此让读者你能够从中学到一些新知识。

你若仔细留意Roger电子邮件下面的评论帖你会看到，@AIActorCritic似乎开始以参数的对偶性(duality of parametrizations)的角度来回答了这个问题，那么我的这个帖子也会沿着对偶性的思路做了些推广，但是要比之更详细一些。

相关链接：

Grosse, Maddison and Salakhutdinov (NIPS 2013) 

http://papers.nips.cc/paper/4879-annealing-between-distributions-by-averaging-moments.pdf

概要

• 在Roger的推特上，他对结果做了一些总结，我将会从这里开始讲述。

• 因发现公式(18)和公式(19)给出了相同的结果，这就是让Roger感到无比惊讶的地方。

• 我首先留意到公式(18)和(19)的右侧部分不仅是可任意的，而且其对应的正是两路径端点之间的Jeffreys散度(对称的KL)。这会给我们某种启示：这里很可能存在一个更普遍意义的规律。

• 然后，为了对这个结果做推广，我将会用更加一般的Bregman散度族来替换KL散度，并且证明若沿着线性路径的无穷小散度做积分，总会在路径端点之间产生对称的散度出来。

• 目前为止，对于这个现象会发生的原因我仍然缺乏直觉上的理解，但是我还是会画一些关于Bregman散度的靓图在本帖中，用以说明问题。

• 然后，我注意到了在凸对偶(convex duality)下Bregman散度的等价性，并证明了公式(18)和公式(19)是推广的Bregman散度中一个对偶对的特殊情形，它们都相当于KL散度。这也就解释了为什么那两个路径给出了相同的结果。

• 最后，我谈及了推广的Bregman散度结构是如何会为分析其他参数空间的线性插值而提供思路。

引言

背景: 作者分析了退火重要性采样AIS(annealed importance sampling)估计量, 其目的是要估计一个难以处理的分布的归一化常数p。 AIS是从较易处理的分布q开始, 通过逐级过渡的分布序列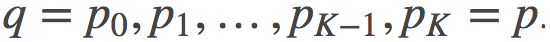到p为结束的空间构造概率分布的路径。这个路径后来被用来构造p的对数分配函数(normalizing constant)的一个估计量。

至关重要的是, 该估计的偏差(bias)取决于我们在两个分布之间选取的某条特定路径: 在q和p之间可以有很多条路径, 这些路径有的很可能会导致更低偏差, 有的可能会得到更高的偏差。在一些简化假设下, 偏差的定义如下给出:

不难看到, 当时, 偏差会趋于0. 但是那篇文章中所考虑的是其精确的渐进行为, 其可从公式(4)中可见一斑:

其中, γ代表了所有可能路径的集合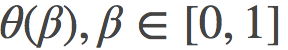，是某一条以θ为参数的路径, 而

是关于θ在θ(β)处的费希尔信息矩阵(Fisher information matrix)。

有意思的是, 如果在分布空间中沿着两条非常不同的路径计算F(γ)(自然参数空间中的一条直线或者时间空间中的一条直线), 你会得到完全相同的值。尽管这些路径明显的有着不同的分布, 正如文章中图1所描绘的。

那么问题就来了：为什么这两条不同的路径, 其偏差却有着相同的渐进行为呢? 

答案的关键可能就是凸共轭对偶（convex conjugate duality）。

初观察

我们首先可以观察到的就是：公式 (18) 和 (19), 其不仅表明这两条路径是等价的, 而且还表明了损失 (cost) 可以用两终端之间的对称KL散度(有时也称为Jeffreys散度)来表示:

为了证明这一点, 我们可以简单的使用如下公式来计算：分别用自然参数η和η′代表的指数分布族之间的KL散度

其中 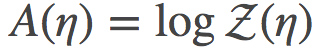是log-partition函数，代表文中关于Pη的时间(moments)。这种观察的角度去分析是很有意思的, 因为我们正在从一个更普遍的角度下的特殊情形中去看问题。

Bregman散度的推广

在凸域上的任何凸函数H都会有Bregman散度, 其在p和q两点之间的定义是:

其中, <>表示内积。我用这里用这个符号来表示而不是矢量积的形式，目的是为了强调p和q可能是函数, 也可能是概率分布, 而并不一定只会是有限维向量。在后文中, 我会将其切换为通常的向量表示法。

关于Bregman散度的例子, 诸如两分布之间的KL散度, 欧式空间中的平方欧氏距离, 两概率分布之间的最大平均差异(maximum mean discrepancy), 等等。想了解更多的话, 我强烈推荐Mark Reid给出的漂亮总结（http://mark.reid.name/blog/meet-the-bregman-divergences.html）。

我们可以替换掉δ中KL散度为一个任意的Bregman散度, 于是就有了如下公式(4)的推广:

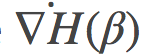
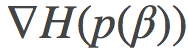
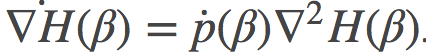
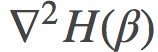
其中是关于β的导数, 推导到第二行时, 我们使用了链式法则，称为度量张量(metric tensor), 它是上文提到过的费希尔信息矩阵的一种泛化推广。

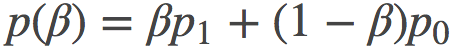
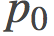
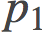
可以证明, 如果我们对p空间做线性差值, 即取某条路径的表示为, 我们就可以将上面的积分式子解析的用路径的端点和来表示:

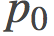
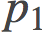
这个最终的表达式就是某路径在端点和之间的对称Bregman散度, 也正是我们在上文中提到的对称KL的一种泛化推广。

在展示这个一般结果是如何能够解释等式 (18) 和 (19) 的等价性之前, 我还花了一些功夫绘制了一些非常好看的图像去可视化我们一直在讨论的Bregman散度。

直观的可视化呈现

下面是关于一些凸势场H下, 两点p和q之间的Bregman散度的图解说明。

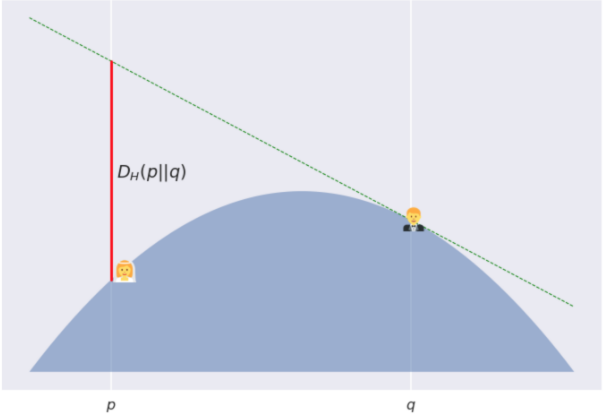
这里有个段子： Poppy 和 Quentin 两人即将结婚，但在神圣的婚礼之前能够见到对方可没那么容易。因此, 他们决定在一个凸起的山丘(从顶部凸起)上共度一个美丽的早晨。Poppy 在坐标p点, Quentin 在坐标q≠p点。这个山丘的表面用−H函数来表示, 其中H是一个凸函数。

严格的说, 正是由于这个山丘是个凸函数, 所以 Quentin 并不能直接看到 Poppy, 除非她会跳! Bregman散度描述的就是 Quentin 跳起来后, Poppy 也不会看到她的最大安全距离。可见山丘越陡, 即曲率越大, Poppy 跳起来看不到 Quentin 的距离范围也就越大。

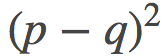
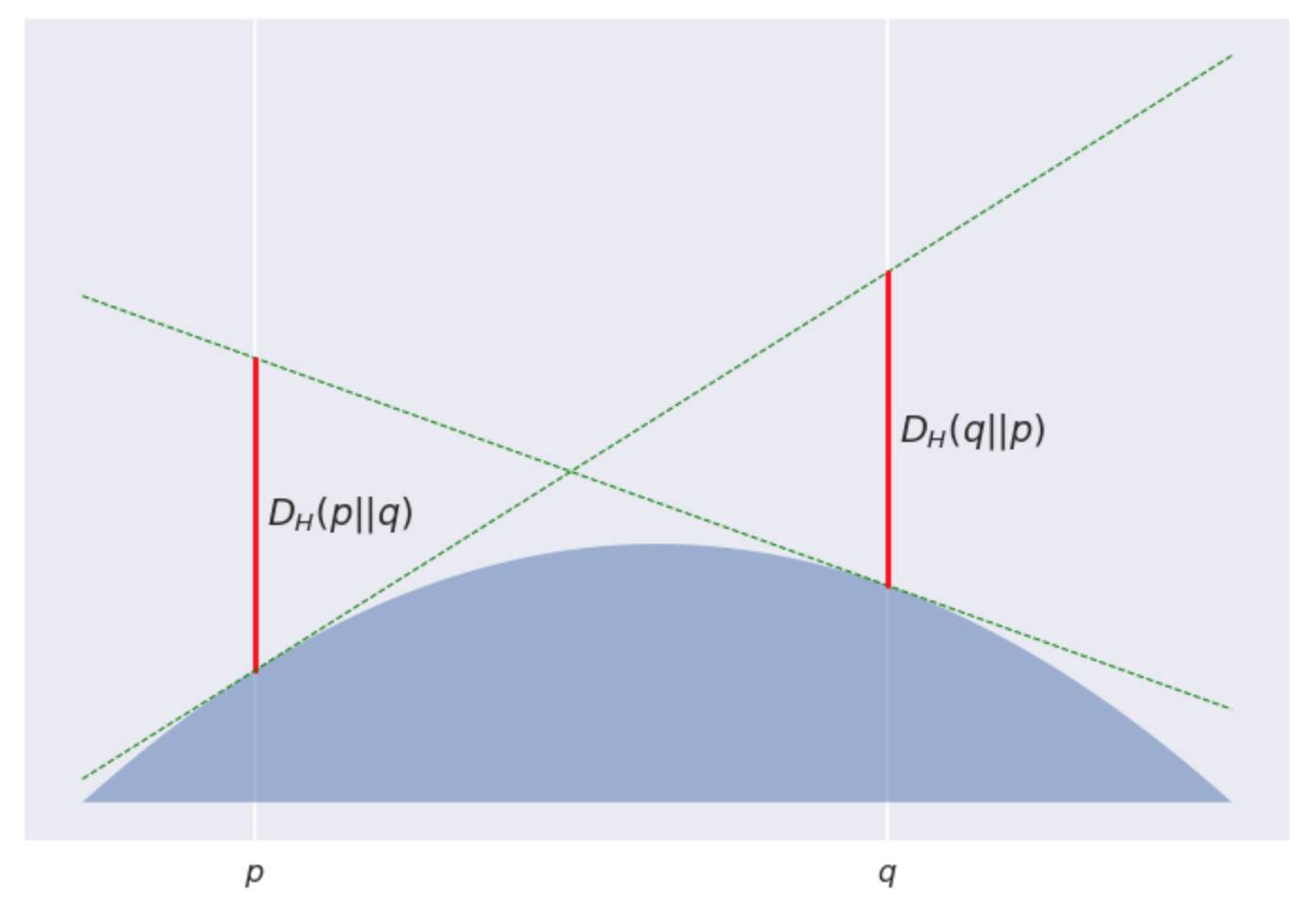
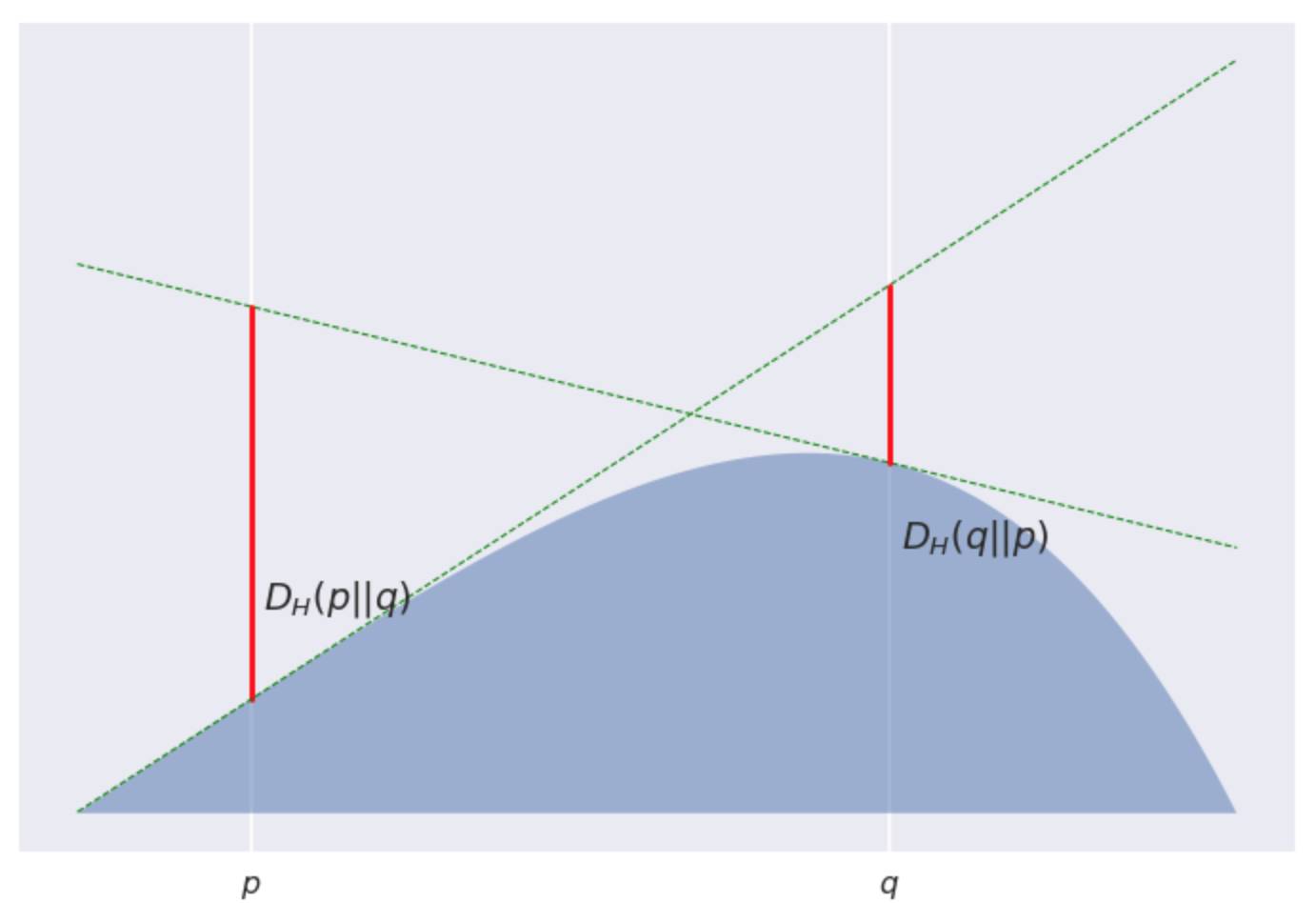
在这个图中, 我用了一个有点无聊的抛物线形的山丘, −H(p)=p(1−p)。由此产生的发散实际上是对称的, 并且其很简单的与平方欧几里得距离成比例:

但这只是个特例, 不是普遍适用的，因为大多数Bregman发散都是不对称的。对于凸函数

来说, 它的图像类似下面这样：

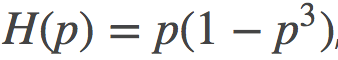
好! 那我们刚刚到底证明了个啥? 可以这样考虑, 我们有一列的伴娘均匀分布在 Poppy 和 Quentin 之间... 好吧, 再如此拿婚礼作比喻恐怕已经不合适了~

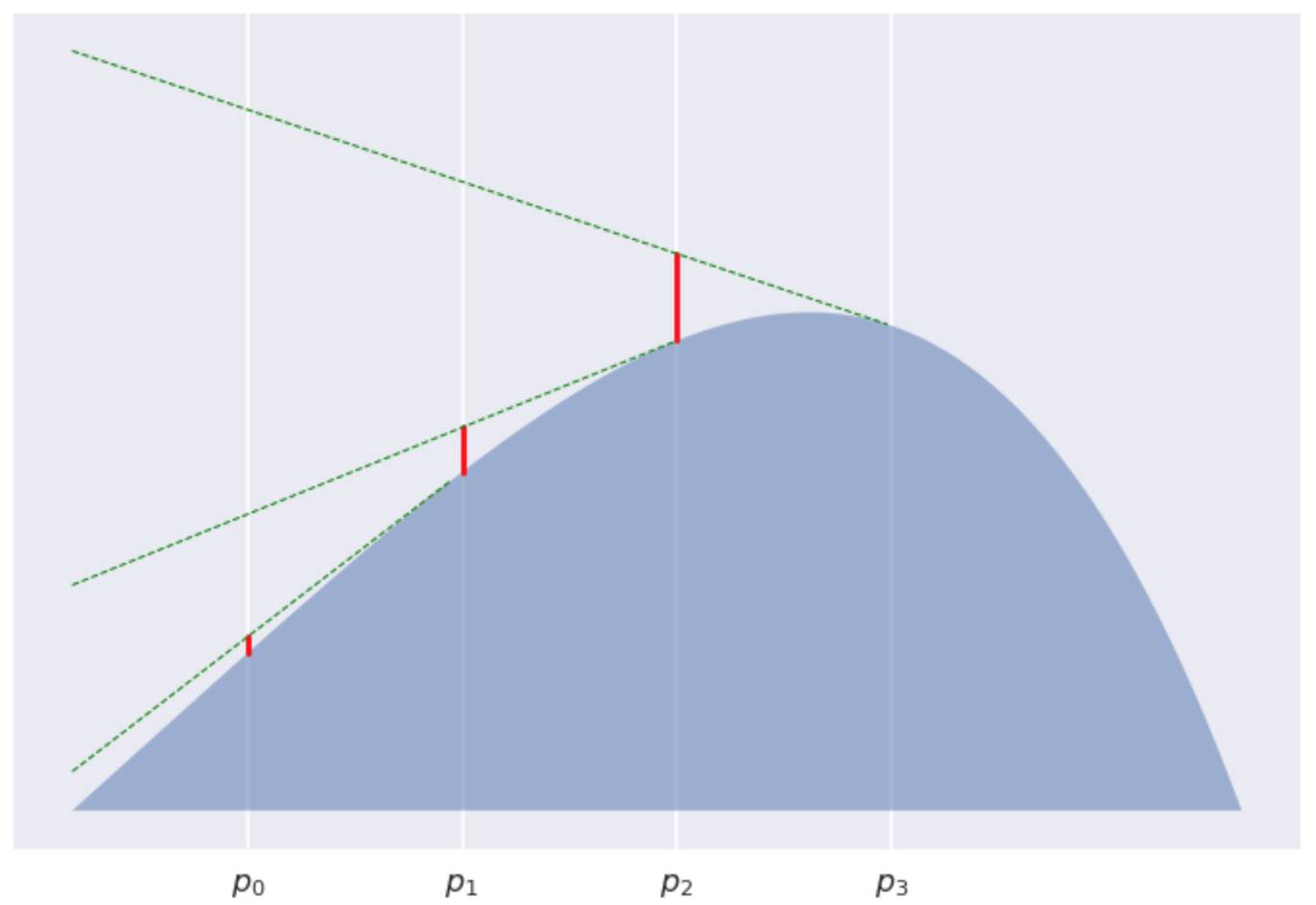
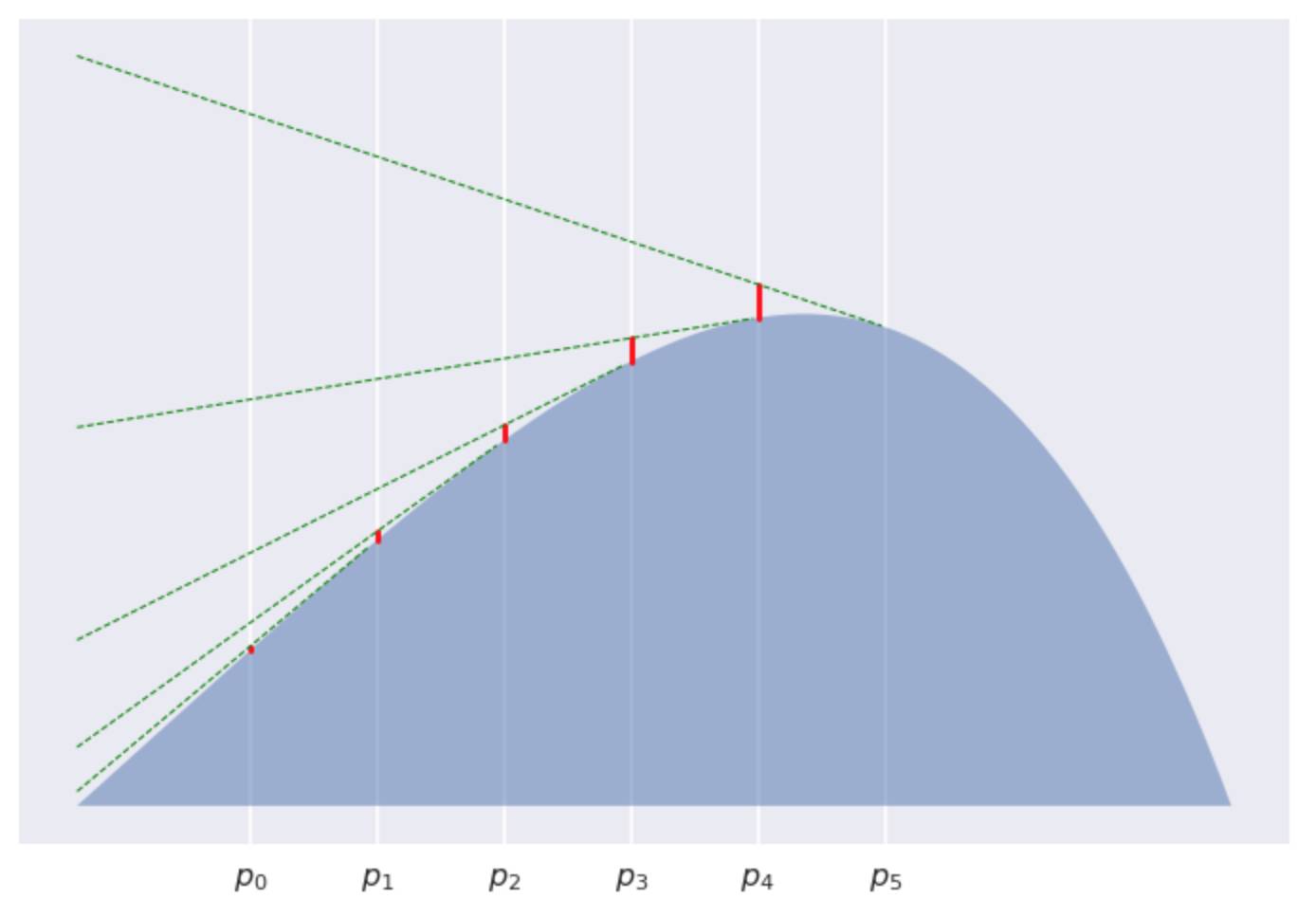
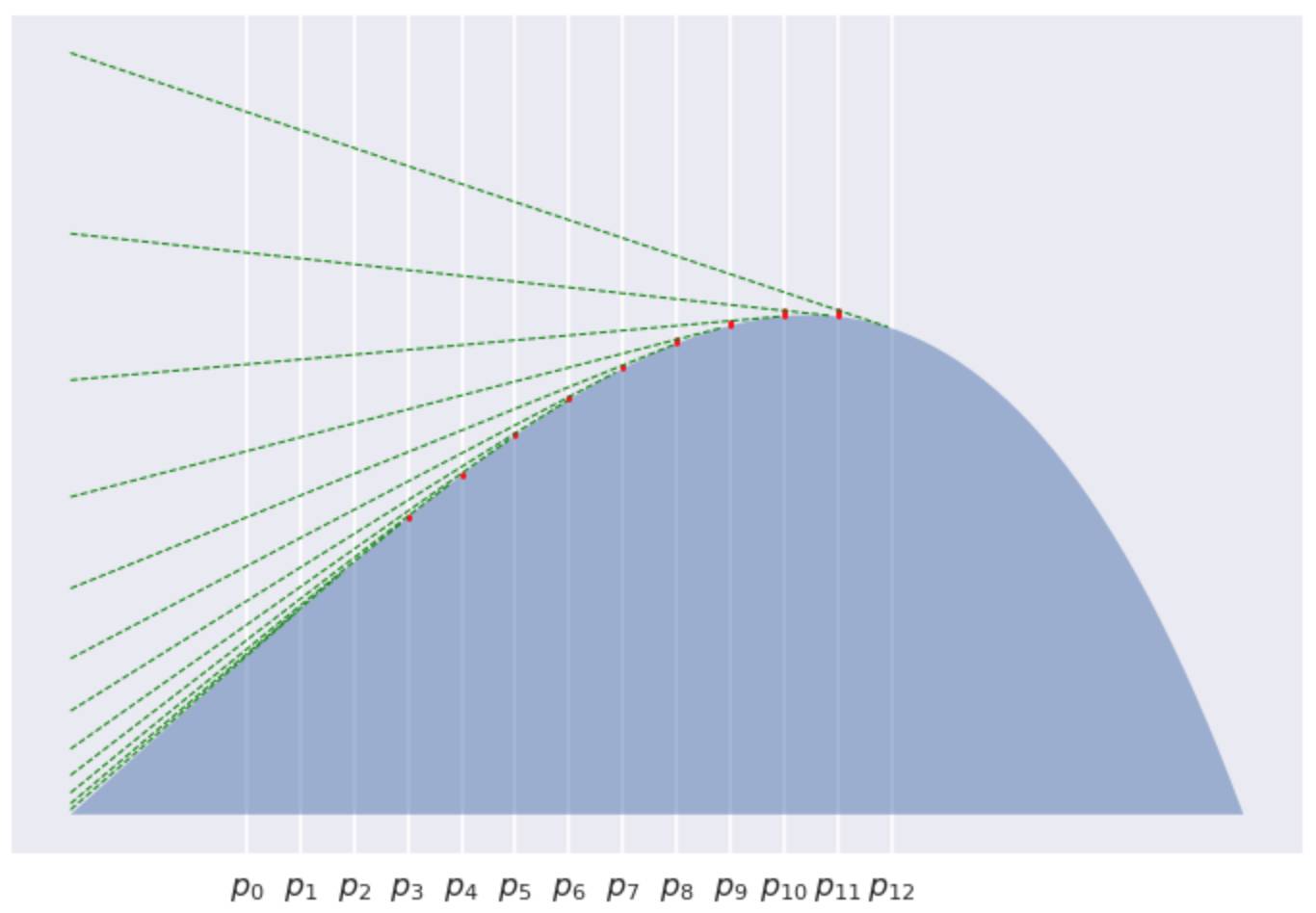
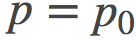
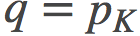
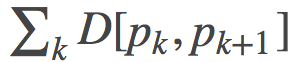
考虑在和之间有一系列的点。现在我们来看一下相邻两个连续点之间的散度之和。这个散度告诉了我们每个Pk至少得跳多高才能看到Pk+1。当K=3时, 我们所讨论是下面红色线部分之和

当K=5

当K=12

很明显的看到, 每个红色线段变得越来越短, 逐渐收敛的到0。如此一来, 我们已经证明了这些红线线段之和的渐进行为如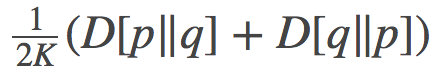。 为何出现这种情况对我来说依然是一个谜。但是我相信会有一个很不错的证明方式。

对偶Bregman散度

我们回过头来看一下为什么在自然参数空间或时间空间中线性插值会给出F(γ)的问题？答案是对偶性(duality)。

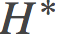
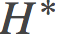
任何一个凸函数H都可以在凸域上定义一个 Bregman 散度。任何一个凸函数H也会有一个凸对偶, 同样的在该凸对偶上, 可以定义其凸域上的一个 Bregman 散度。

一般来说, 这二者的凸域是不一样的。而且，这个对偶散度与原散度之间有如下的等价关系：

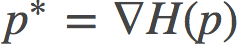
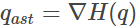
其中和分别称为p与q的对偶参数(dual parameters).。

得益于凸性(convexity)，这个参数与其对偶参数之间存在一一对应的映射关系。p和q有时也被叫做原始参数(primal parameters)， 但这个命名我认为太过随意了，因为该共轭对偶关系事实上是对称的。

根据我们对对偶性的理解, 让我们来看看我们之前得到的公式：

上面的公式中，我们可以观察到原始参数和对偶参数之间的双线性关系。

指数族中的共轭对偶

现在我们来考虑一个指数族的形式：

其中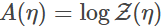是log分割函数。由于A是一个关于η的凸函数, 我们就可以在以(凸)log分割函数A诱导的自然参数η作为坐标系统来定义 Bregman 散度: 

（可以注意到这个表达式和我之前用的KL散度是多么的相像啊！）

这个用η表达的对偶参数可以证明就是时间参数s：

上式中间的等号利用了指数族的一个众所周知的性质, 其证明的过程类似于如何获得增强梯度估计器(REINFORCE gradient estimator)。 利用这个等价关系，我们可以重写上面的散度：

如果我们把自然参数η看做原始参数, 那么时间参数s就是其对偶参数。如往常一样, 在原始参数和对偶参数之间存在一一对应的关系，因此, 利用凸共轭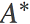，我们可以定义另一个 Bregman 散度在时间坐标s如下：

事实证明, 这个凸共轭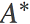是以时间 s参数的分布的Shannon的负熵(这已经超过了本帖所讨论的范围, 详情请参考this book chapter-http://onlinelibrary.wiley.com/doi/10.1002/9781118857281.ch9/summary)。

所以, 现在我们有两个 Bregman 散度, 一个是定义在η原始参数空间, 另一个定义在其s对偶空间上。两个散度是等价的, 而且在此情形下, 它们都等价于相应分布之间的KL散度：

所以, 现在当我们把这些都放在一起讨论, 我们就理解了为什么公式(18)和(19)会给出相同的结果了。

如果我们在原始参数 η(0) η(1)间做线性差值, 我们就会得到某路径的损失: 

类似地, 在时间空间s(0)和s(1之)间差值, 我们就可以得到: 

于是, 根据A和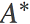的对偶性, 我们可以得知上面两个式子是等价的, 并且都在相应的分布下等价于对称KL散度。

有趣的是, 这个等价性也表明, 在分布空间的线性差值也将给出相同的结果, 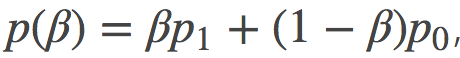。这将通过两个分布之混合插入在p0和p1之间来实现, 尽管这样做可能并没有什么实际意义。

其他参数空间中的解释

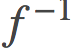
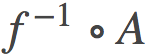
通过与自然参数相关的凸运算方法，这一套解释框架为我们研究参数空间中的线性插值提供了可能性。只要f是可逆的，并且具有正定的雅可比行列式，我们都可以使用凸函数来定义θ空间中的Bregman散度。 不过，我还并不确定这是否有什么实际用处或者可以从中得到任何其他的见解。

总结

这就是我尝试深入理解Roger的论文中的定理2所做的工作了。我的这个帖子可能并没有让结果看上去那么令人惊讶，只是将我们的理解略做了些变相转换。 

其可以简述如下：

1. 沿着线性路径积分Bregman散度，我们得到了路径端点之间的对称Bregman散度;

2. 对于指数族，KL散度可以等效地表示为自然参数空间中的Bregman散度或者时间空间中的Bregman散度。这些散度的标量势是彼此的共轭对偶，因此它们是等价的。

3. 因此，由于双Bregman散度的等价性，将KL散度沿着线性路径在η或β空间中积分会产生相同的结果。

原文链接 http://www.inference.vc/grosses-challenge/

热文精选

谈深度学习必谈计算力！如何成为一名异构并行计算工程师？

干货 | 成为一名推荐系统工程师永远都不晚

AI校招程序员最高薪酬曝光！腾讯80万年薪领跑，还送北京户口

谷歌AI正式来中国了，机器学习三大职位正在招聘...如果你想跟李飞飞一起工作的话

算法还是算力？周志华微博引爆深度学习的“鸡生蛋，蛋生鸡”问题

详解 | 如何用Python实现机器学习算法

经验 | 如何高效学Python？

深度学习高手该怎样炼成？这位拿下阿里天池大赛冠军的中科院博士为你规划了一份专业成长路径

深度学习框架哪家强？MXNet称霸CNN、RNN和情感分析，TensorFlow仅擅长推断特征提取

如何成为一名全栈语音识别工程师？

Twitter大牛写给你的机器学习进阶手册