基于 Carsim 2016 和 Simulink的无人车运动控制联合仿真（三）

简介

该节将简要说明模型预测控制的基本原理

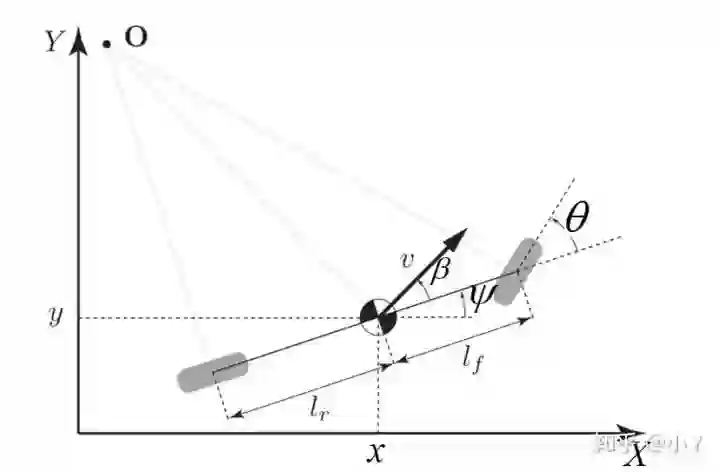
1、运动学模型

使用自行车模型作为运动学约束

2、优化问题建模

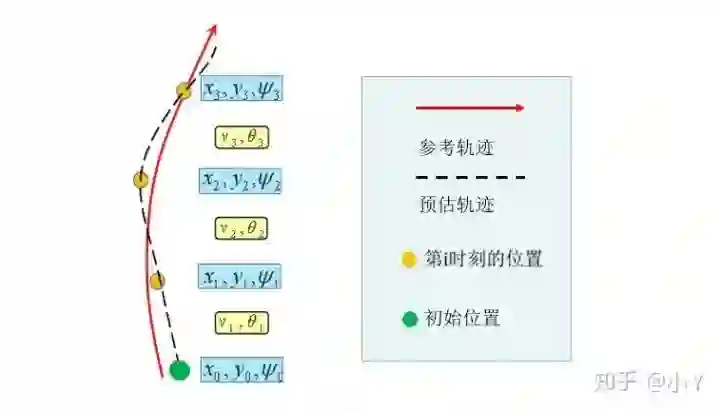
上图为模型预测控制的一个示意图，在当前位姿下，使用运动学模型对后续n个时刻的位姿进行估计，使用非线性优化器求解出cost最小的控制量v和delta

该模型假设速度恒定，即只进行横向的控制，需要进行纵向控制时，请参考优达学城上的方法

目标函数

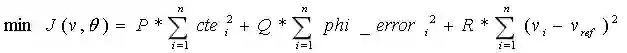
其中：

P,Q,R 为权重矩阵

cte为无人车的横向误差

phi_errror为无人车的姿态误差

等式约束项

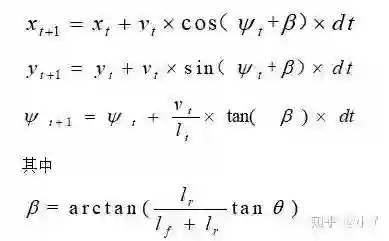
不等式约束项

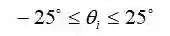
3、单步的MATLAB程序

主程序

clc
clear all

NP = 10;   %预测周期数
dt = 0.05; %预测周期

x_start     = 0;
y_start     = x_start + NP;
phi_start   = y_start + NP;
cte_start   = phi_start + NP;
ephi_start  = cte_start + NP;
delta_start = ephi_start + NP;
% 状态变量和控制变量的总个数
m = 6 * NP ; 
% 向量var前10个表示10个时刻x_start，第11到20个表示10个时刻y_start，第21到30个表示10个时刻phi_start，后续以此类推
var = zeros(m,1);


% 损失函数
func  = @(var)cost_function( var,NP,dt ); 
% 约束条件
nlcon = @(var)nonlconstrict( var,NP,dt ); 
% 各个约束的上下界
cl = zeros( 6*NP+1,1 ); 
cu = zeros( 6*NP+1,1 );
% 方向盘转角的上下界（弧度）
for i = (5*NP+1):6*NP
    cl(i) = -0.45;
    cu(i) =  0.45;
end
% 求解的初始化
state_intial = zeros(m,1);
% 求解器的设置
opts = optiset('solver','IPOPT','display','iter','maxiter',50,'maxtime',0.5);
% Create OPTI Object
Opt = opti('fun',func,'nl',nlcon,cl,cu,'x0',state_intial,'options',opts);
% Solve the NLP problem
[A,fval,exitflag,info] = solve(Opt,state_intial)
% 向量A为所求的解

目标函数

function cost = cost_function(var,NP,dt)

    x_start     = 0;
    y_start     = x_start + NP;
    phi_start   = y_start + NP;
    cte_start   = phi_start + NP;
    ephi_start  = cte_start + NP;
    delta_start = ephi_start + NP;

    cte = 0;
    ephi = 0;
    delta = 0;
    for i = 1:1:NP
        cte = cte + var( cte_start+i )^2;
        ephi = ephi + var( ephi_start+i)^2;
    end
    for i = 1:1:NP-1
        delta = delta + ( var( delta_start+i+1 ) - var( delta_start+i ) )^2;
    end    

    cost = 1*cte + 1 * ephi + 100*delta;
end

约束函数

function c = nonlconstrict( var,NP,dt )

    x_start     = 0;
    y_start     = x_start + NP;
    phi_start   = y_start + NP;
    cte_start   = phi_start + NP;
    ephi_start  = cte_start + NP;
    delta_start = ephi_start + NP;

    x_0     = 0;
    y_0     = 0;
    phi_0   = 0;
    v       = 5;
    delta_0 = 0;
    lf      = 3;

    c = zeros( 6*NP+1,1 );
    for i = 1:1:NP
        if i == 1
            c( x_start + i )    =  var(x_start + i )    -  x_0   -  v * cos( phi_0 ) * dt;
            c( y_start + i )    =  var(y_start + i )    -  y_0   -  v * sin( phi_0 ) * dt;
            c( phi_start + i )  =  var(phi_start + i )  -  phi_0 -  v /lf * tan(  delta_0  ) * dt; 
            c( cte_start + i )  =  var(cte_start + i ) -   3 + v * sin(phi_0) * dt;
            c( ephi_start + i ) =  var(ephi_start + i) -   0 + v/lf * delta_0*dt;
            c( delta_start + i )=  var(delta_start + i);
            c( delta_start + i + NP)=  var(delta_start + i) -  delta_0 ;

        else
            c( x_start + i )    =  var(x_start + i )   -   var(x_start + i-1 )     -  v * cos( var(phi_start + i-1) ) * dt;
            c( y_start + i )    =  var(y_start + i )    -  var(y_start + i-1)     -   v * sin( var(phi_start + i-1) ) * dt;
            c( phi_start + i )  =  var(phi_start + i )  -  var(phi_start + i-1)   -   v/lf * tan(  var(delta_start + i-1)  )  * dt;
            c( cte_start + i )  =  var(cte_start + i ) -   3 + v * sin( var(phi_start+i-1) ) * dt;
            c( ephi_start + i ) =  var(ephi_start + i) -   0 + v/lf * var(delta_start + i-1) * dt;  
            c( delta_start + i )=  var(delta_start + i);
        end     
    end
end

参考资料

https://github.com/ksakmann/CarND-MPC-Project

https://github.com/jeremy-shannon/CarND-MPC-Project

欢迎来到泡泡论坛，这里有大牛为你解答关于SLAM的任何疑惑。

有想问的问题，或者想刷帖回答问题，泡泡论坛欢迎你！

泡泡网站：www.paopaorobot.org

泡泡论坛：http://paopaorobot.org/bbs/

泡泡机器人SLAM的原创内容均由泡泡机器人的成员花费大量心血制作而成，希望大家珍惜我们的劳动成果，转载请务必注明出自【泡泡机器人SLAM】微信公众号，否则侵权必究！同时，我们也欢迎各位转载到自己的朋友圈，让更多的人能进入到SLAM这个领域中，让我们共同为推进中国的SLAM事业而努力！

商业合作及转载请联系liufuqiang_robot@hotmail.com