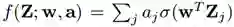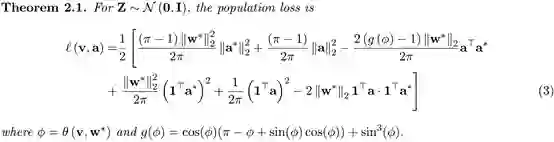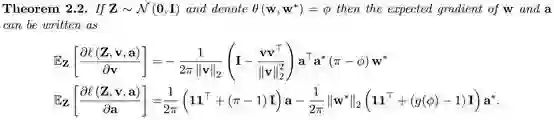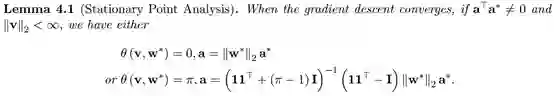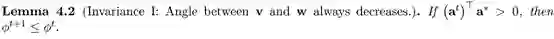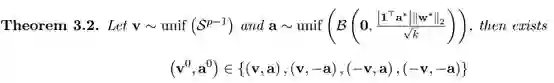Facebook FAIR实验室田渊栋等人最新论文：别担心深度网络中的虚假局部极小值

2017 年 12 月 8 日 专知专知内容组（编）

点击上方“专知”关注获取专业AI知识!

【导读】近日，Facebook FAIR实验室、南加州大学与卡耐基梅隆大学提出《Gradient Descent Learns One-hidden-layer CNN: Don't be Afraid of Spurious Local Minima》文章证明了在高斯分布的输入和L2损失的条件下（1）对于两层的神经网络，存在虚假的局部极小，但是梯度下降可以以一定概率收敛到全局最优点，给出了单隐层神经网络梯度下降的多项式收敛保证。（2）梯度下降的训练过程分为两个部分，一个缓慢的开始阶段和一个线性速率的收敛过程。以下是相关论文介绍。

▌论文简介

论文：Gradient Descent Learns One-hidden-layer CNN: Don't be Afraid of Spurious Local Minima

这篇文章分析了一种非重叠的ReLU激活的单隐层神经网络：

证明了对于高斯输入Z，存在非全局最小值的虚假的局部极小值。令人惊奇的是，在存在局部极小值的情况下，可以证明，随机初始化的权值+权值正则化仍然能以恒定的概率（任意精度）到达全局最优。我们同样可以证明，这个相同的过程可以以恒定的概率收敛到虚假的局部极小值，这说明局部极小值在梯度下降的动态过程中起到了重要的作用。量化的分析表明，梯度下降有两个阶段：开始比较慢，然后几轮迭代后收敛速度变快。

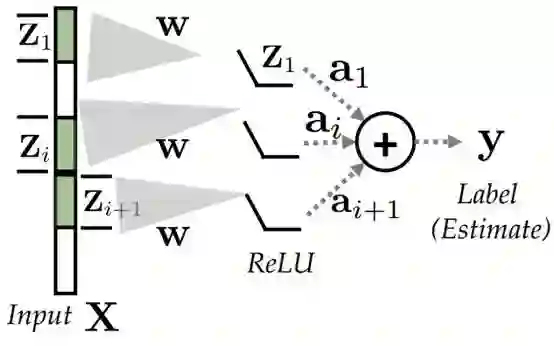
图1（a）：拥有未知的非重叠滤波器和未知输出层的CNN，第一个隐层，w作用于输入x中的非重叠的部分，然后再通过一个ReLU激活函数，最终的输出为隐层输出与向量a的内积。

图1（b）：这是上图（a）中CNN收敛性的图示，卷积大小p=20，非重叠块数目k=25 。图中展示了收敛到全局最优和虚假的局部极小的情况。其中前50epoch收敛速度很慢，之后梯度下降线性收敛。

图1：CNN设置与使用梯度下降进行网络学习的收敛速度。

▌模型简介

我们也可以看到训练算法的伪代码，其和普通的梯度下降没有区别。

本文证明了在高斯分布的输入和l2损失的条件下：

1. 梯度下降的多项式收敛保证：

对于两层的神经网络，存在虚假的局部极小，但是梯度下降可以以一定概率收敛到全局最优点。首次给出了单隐层神经网络梯度下降的多项式收敛保证。

证明首先利用高斯分布的旋转不变性定义了损失函数。

然后得到了梯度的期望值

首先

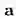
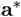
该引理表明，当梯度下降收敛，且与不正交，则必定收敛于全局最优点或者局部极小值点中的一个。

这个引理表明，当时，我们会向全局最优点收敛。这意味着我们要分析

然后就可以证明

这个定理表示，我们只需要遍历4种形式的向量对，就可以高概率地得到全局最优点。

2. 梯度下降过程分析：

这个引理表明，收敛速度取决于两个重要的量和，

开始的时候，这两个量都很小。经过一段时间后，，从而得到，进入第二个收敛阶段。

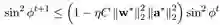
于是我们可以证明，梯度下降的训练过程分为两个部分，一个缓慢的开始阶段和一个线性速率的收敛。

▌结论和未来方向

本文给出了用于学习一个隐藏层卷积神经网络的随机初始化梯度下降算法的第一多项式收敛保证。结果揭示了一个有趣的现象，即随机初始化局部搜索算法可以收敛到全局最小值或假的局部极小值，并且这两种情况的发生具有恒定的概率。文中对梯度下降动态性（gradient descent dynamics）给出了一个完整的定量描述来解释两阶段的收敛现象。这里我们列出一些未来的方向。

本文的分析集中在高斯输入的整体损失。在实践中，人们使用（随机）经验损失的梯度下降。[Mei et al，2016。Soltanolkotabi，2017。Daskalakis et al，2016。Xu et al，2016] 中的结果对于将文中的结果推广到经验版本是有用的。一个更具挑战性的问题是如何扩展梯度动态分析的旋转不变输入分布。Du et al[2017b] 在单层卷积神经网络的某些结构输入分布假设下证明了梯度下降的收敛性。将他们的见解带入本文的环境将会很有趣。

另一个有趣的方向是将文中的结果推广到更深更广的体系结构。具体而言，一个开放的问题是在什么条件下随机初始化梯度下降算法可以学习一个隐层全连接的神经网络或一个多核卷积神经网络。现有的结果往往需要很好地进行初始化 [Zhong et al，2017a，b]。我们相信本文的观点，特别是文中4.1节中的不变原理，有助于理解这些设置中基于梯度的算法的行为。

论文：Gradient Descent Learns One-hidden-layer CNN: Don't be Afraid of Spurious Local Minima

▌摘要

这篇文章分析了一种非重叠的ReLU激活的单隐层神经网络，例如，其中卷积权值w和输出权值a是要学习的参数。本文证明了对于高斯输入Z，存在非全局最小值的虚假的局部极小值。令人惊奇的是，在存在局部极小值的情况下，可以证明，从随机初始化的权值开始，具有权值正则化的梯度下降仍然能以恒定的概率（通过多次重启，其可以被提升至任意精度）到达全局最优。