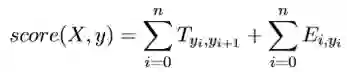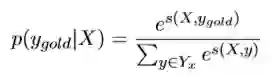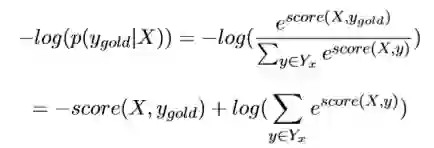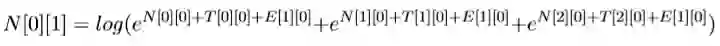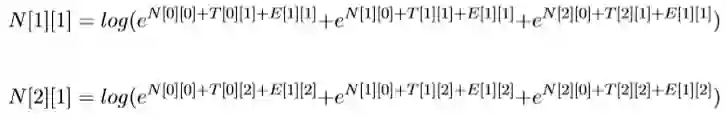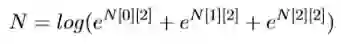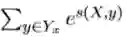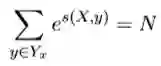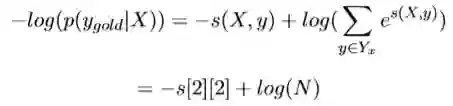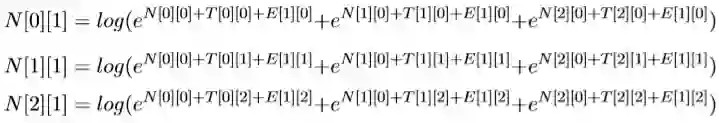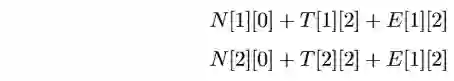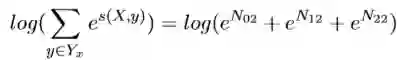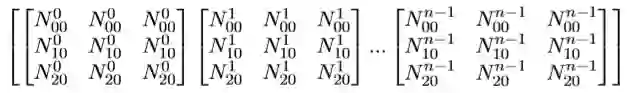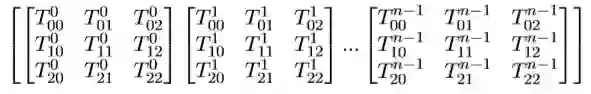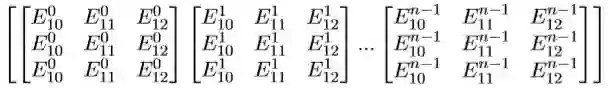基础 | 长文详解基于并行计算的条件随机场

阅读大概需要10分钟

之前写过CRF的详解，只是为了让大家详细了解下原理，但是那种是没有优化的，速度很慢。在实际应用中，还是需要用到batch，也就是需要用到GPU的，那么此时并行计算就变得极为重要。在研究到一定的程度上，困住你的不是算法本身，而是时间。同一件事，当然是越快越好。此时困住你的就是加速问题。

我认为的加速大概分为两种：

1. 算法的本身的速度。

2. 程序中的循环怎么改为矩阵计算，也就是并行计算。

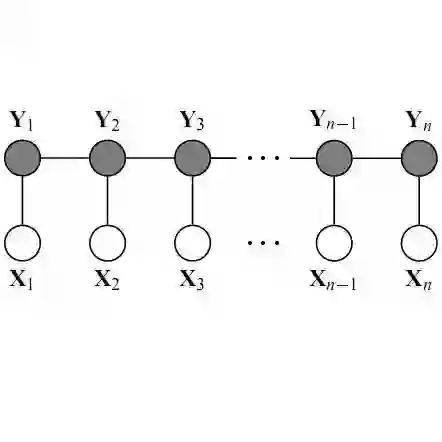
这里先以条件随机场CRF为例，详细讲解CRF原理和如何加速的并行计算。

1.概述

CRF（Conditional Random Field），中文被翻译为条件随机场。经常被用于 序列标注，其中包括词性标注，分词，命名实体识别等领域。但是为什么 叫这个名字呢？下面看完了基本也就明白了！那我们继续吧。

2.理论

我们以 词性标注 为例，先介绍下词性标注的概念：

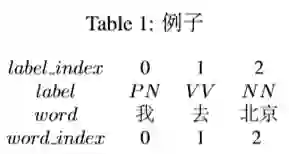
这个表示 词:词性，分别为 我:PN，去:V V ，北京:NN。

Table1就是word和label数字化后变成word index，label index。最终就 变成Table2的形式：

上述是标准金标，也就是正确答案，但是实际上电脑预测的不会是正 确的。因为label有3种，每一个字被预测的label就有3种可能，为了数字化 这些可能，我们从word index 到label index 设置一种分数，叫做发射分 数emit，简化为E。 

word index 的2到label index的2，像不像发射上去的？此时的分数就记 作发射分数E[2][2]。

 另外，我们想想，如果单单就这个发射分数来评价，太过于单一了， 因为这个是一个序列，比如前面的label为1代表V V 动词，那此时的label被 预测的肯定不能是V V ,因为动词后面不能接动词，所以知道前一个label转 向后一个label可能性会增加准确率，所以这个时候就需要一个分数代表前 一个label 到此时label 的分数，我们叫这个为转移分数，即T。如图，横 向的label到label，就是由一个label到另一个label转移的意思，此时的分数 为T[1][1]。

假设word index = i到label index = j的分数为s[i][j]，则

s[0][0] = E[0][0]

因为word index = 0前面没有word index了，所以s[0][0]就为发射分数E[0][0]。 word index = 1到label index = 1的分数s[1][1]为E[1][1]+T[0][1]。但是CRF 为了全局考虑，将前一个的分数也累加到当前分数上，这样更能表达出已 经预测的序列的整体分数，则：

s[1][1] = s[0][0] + E[1][1] + T[0][1]

所以，s[2][2]也就很容易了：

s[2][2] = E[0][0] + E[1][1] + T[0][1] + E[2][2] + T[1][2] 

因为s[2][2]已经为最后的词的的分数，所以该s[2][2]为金标score({我 去 北 京},{PN VV NN})即score({0 1 2},{0 1 2})的最终得分。最后的公式总结为：

其中X为word index序列，y为预测的label index序列。

因为这个预测序列有很多种，种类为label的可重复排列组合大小。其中 只有一种组合是对的，我们只想通过神经网络训练使得对的score的比重在总体的所有score的越大越好。而这个时候我们一般softmax化，即：

其中分子中的s为label序列为正确序列的score，分母为每种可能的score的 总和。 

这个比值越大，我们的预测就越准，所以，这个公式也就可以当做我们 的loss，可是loss一般都越小越好，那我们就对这个加个负号即可，但是这个最终结果是趋近于1的，我们实验的结果是趋近于0的，这时候log就派上 用场了，即：

当然这个log也有平滑结果的功效。

3.计算所有路径的得分

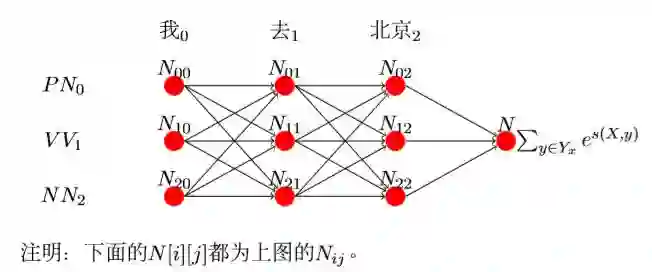
loss的分子在上面已经求出来了，现在就差分母了，而计算所有预测序列可能的得分和也就是计算所有路径的得分。我们第一种想法就是每一种可 能都求出来，然后累加即可。可是，比如word序列长为10，label种类为7， 那么总共需要计算10^7次，这样的计算太耗时间了。那么怎么计算的时间快呢？这里有一种方法，就是每个节点记录之前所有节点到当前节点的路径 总和。如图：

解释下这个图：

 第一列： 

首先说下，因为‘我’是第一列，前面没有别的词，所以就不用加上前 面的值。继续说，N[0][0]表示‘我’选择PN的得分，N[1][0]表示‘我’选 择V V 的得分,N[2][0]表示‘我’选择NN的得分而该得分只有发射得分，所以为：

 N[0][0] = E[0][0] 

同理，得： 

N[1][0] = E[0][1] N[2][0] = E[0][2] 

再来分析第二列:

 N[0][1]表示前一个选择PN的得分+‘去’选择PN的得分（‘去’选 择PN的得分为T[0][0]+E[1][0]），前一个选择V V 的得分+加上‘去’选 择PN 的得分，加上前一个选择NN的得分+‘去’选择PN的得分。公式为： 

类推： 

再类推第三列： 

最后一列求完了，因为每个节点都包含了该节点之前所有节点到该节点的 可能路径，因为现在的 

的总和就是所有路径的总和，也就是我们要求的损失函数里面的

即为：

4.得出具体损失函数

最终的我们的 损失函数 求出来了： 

这样我们就能根据损失函数反向传播梯度，更新T E参数了。

5.batch

上面的那种求总和的方法，还有一种好处就是可以加快并行计算，也就刚 好能做多个句子的batch批处理。先说什么是并行计算，字面意思就能理 解，并行，并排行进，大家同时进行的意思，同时进行的前提条件是需要 用到的东西都已经准备好。放在计算机里的意思就是当前运行的程序需要 的数据都已经准备好了。那我们来看看我们的数据怎么能并行计算吧，我 拿出来一列数据来看看（先说下为什么拿出的是一列，而不是一行，因为 一列所需要的数据前一列都已经计算过了，而一行不具备这样的条件）， 比如第二列：

但是这样或许看不到什么效果，我来整理下，去掉log，去掉e，只提取数 据： 

我们先看N这三组数据，发现每组里面N都是一样都为N[0][0],N[1][0],N[2][0]， 所以我们可以设定矩阵N为： 

我们看到矩阵N第0维循环变化，第1维不变，但是上面的只是一组数据， 我们需要三组，所以我们对该N进行二维扩展，也就是列复制： 

再看T，第一组为T[0][0],T[1][0],T[2][0]，第二组为T[0][1],T[1][1],T[2][1]， 第三组为T[0][2],T[1][2],T[2][2]。我们能其实够很明显的看出第一组为T的3∗ 3矩阵第0列，剩下的分别为第1列，第2列，即矩阵T为： 

最后同理我们看E，我们会观察到它和N的情况相似，但是E第0维不变， 第1维是循环变化，所以是行复制： 

我们会发现，矩阵N T E的第一列按位相加的结果刚好是N[0][1]，同理的，第二列，第三列分别按位相加分别得N[1][1]，N[2][1]，即： 

同 理，求出N_02 N_12 N_22，然后：

上面的只是表示一个句子的计算，我们为了加快速度，或者使用GPU的 时候，需要用到batch，那么batch里的上述N T E是怎么个存在形式呢？ 以batch = n为例：N数据格式为： 

T数据格式为： 

E数据格式为： 

其中，X^i_j中的i表示batch里的第i组矩阵，j表示batch里的第i组中位置为j的 数据。

6.预测过程

上面是 Encoder编码 过程，训练完了，该看看训练的效果了，这里预测的过 程叫做 Decoder解码 过程。这时候N E T都是固定了的，不会再变化。我们 的目的是，选取可能性最高的，又因为可能性最高在这里表示得分最高， 然后根据最高的得分，我们向前一个一个的选取每次前一个最高得分的节 点，最终这些所有的节点就是我们的最后的预测序列。这个过程是不是很 熟悉的感觉，对就是我们的 动态规划 算法，但是在这里叫 维特比 算法。我 们来走一遍过程： 

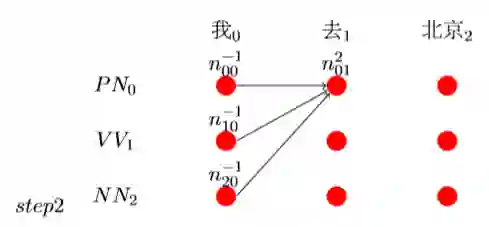
每个节点选取得分最高的路径并记录得分和选的哪条路径：其中n^s_ij中的s表示前一条路径，没有的就是−1，nij表示前节点到当前节点的最佳得 分。 此时

比如此时预测n_20 + E[1][0] + T[2][0]为最高的，则记录n_01 = n_20 + E[1][0] + T[2][0]且路径为2,综上记为n^2_01:

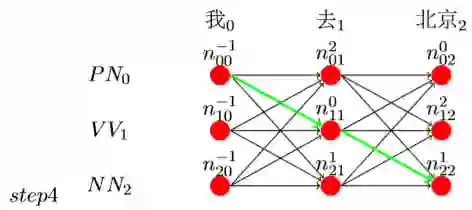
同理，我们假设有了step3的最终结果。

在最后我们假如n_22最大，而且它的前一个路径为1，则看到n_11的前一 个路径为0，而且n_00的前一个路径为−1，表示结束，则整个路径就有了， 即为n_00− > n_11− > n_22，如图step4：

由step4得，最终(’我’，’去’，’北京’)的预测结果为：

(’我’− > PN，’去’− > V V ，’北京’− > NN)。

推荐阅读

基础 | TreeLSTM Sentiment Classification

基础 | 详解依存树的来龙去脉及用法

基础 | 基于注意力机制的seq2seq网络

原创 | Simple Recurrent Unit For Sentence Classification

原创 | Attention Modeling for Targeted Sentiment

原创 | cw2vec理论及其实现

基础 | 中英文词向量评测理论与实践

欢迎关注交流