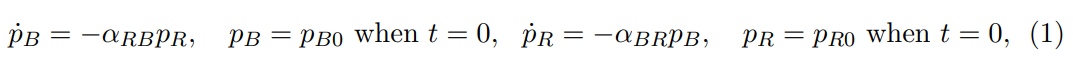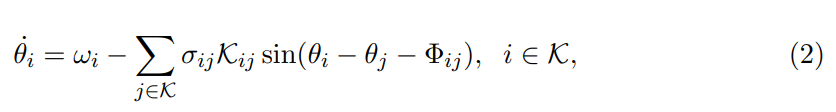论文|《用数学建模整合作战功能：战斗、机动和C2》，2023最新30页论文

战争结果很少只以单个作战部队要素的数量和质量为特征。通过有效的指挥和控制（C2）来调动和适应各部队要素的能力可以使较小或较弱的部队战胜拥有更多资源和火力的对手。在本文中，我们将经典的兰彻斯特（Lanchester）作战模型与网络上相位振荡器Sakaguchi-Kuramoto模型结合起来，创建了一个灵活的网络化兰彻斯特式C2模型来表示军事交战。因此，该数学模型统一了军事作战的三个 "功能"：火力、机动和C2。我们考虑了三个说明性的用例，并表明对一个简化模型的分析处理可以描述整个系统中的全球效应。对于不同类的兵力，我们观察到，在内部组织耦合、资源机动性和甚至较弱的杀伤力之间有适当的平衡，部队可以适应性地克服最初较强的对手。

自从有组织的战争开始以来，拥有战略和战术可使指挥官能够击败数量上占优势的敌人。特别是，与纯粹的消耗战相比，超越对手力量的能力可以为取得更加决定性的结果提供机会。我们建议通过耦合微分方程对这些动态进行数学建模，整合战斗、机动和指挥与控制（C2）。

拿破仑可以说是最著名的，也是最具代表性的例子，在战役层面上，他能够以分布式和集中式方式转换指挥他的部队，然后在一个决定性的点上，同步化他胜利的关键因素。也有一些更局部的例子，即一支巧妙分散、敏捷和反应迅速的部队能够击败数量上占优势的对手。在公元前197年的Cynoscephalae战役中（Polybius，1927年），操纵战术分队的卓越机动性和可控性使罗马人战胜了马其顿方阵和重骑兵。在1346年的Cr´ecy战役（Reid，2007年）中，随着英国长弓的引入，战术上得以有效地扰乱（通常是毁灭性的）重骑兵的冲锋，从而使英国人击败了数量上占优势的法国军队。二战中德国国防军的闪电战和第一次海湾战争中的联军都再次证明了机动性思想。

我们提出的模型建立在兰彻斯特方阵(定向火力)模型的基础上(兰彻斯特，1916)，

其中，αRB、αBR分别给出红方和蓝方部队的战斗力或致死率，pR、pB分别为红方和蓝方的资源数量。作为一个常数系数的线性常微分方程系统，等式（1）中的守恒量是可以分析解决的，这意味着致死率和初始资源决定了战斗的结果。

请注意，其他模型缺乏连续的战斗动态，如Blotto上校博弈（Roberson，2006），或海战Hughes salvo模型（Hughes，1995）。兰彻斯特模型已经被扩展到适合不同历史背景下的经验数据（Bracken，1995）（也见（Fricker，1998）和（Lucas & Turkes，2004）），被（MacKay，2009）和（Kress等人，2018）扩展到最近的混合部队变体，被用于人工智能玩实时战略游戏Starcraft（Stanescu等人，2015）和不对称游击战（Deitchman，1962）和（Schaffer，1968）。

在所有这些中，指挥和机动的功能被埋没在战斗力常数中。当对两支部队在漫长的交战中战略不变的数据进行拟合时，这是合理的，但即使是简单的社会动物也很少如此，正如（Adams & Mesterton-Gibbons, 2003）和（Plowes & Adams, 2005）中讨论的那样。也很难先验地估计一支部队的战斗力，或评估战斗力对组织变化的稳定性。更重要的是，信息和通信技术在组织不同的（例如，来自不同军种的）部队成员的作用，使得网络范式对当代和未来的战争具有强大的作用。这导致了近几十年来被称为 "网络中心战"（Alberts等人，1999年）的主张，将网络连接、部队要素的自我同步化和有效的军事成果联系起来。尽管兰彻斯特模型被视为网络化赛博攻击和防御的抽象模型（Liu等人，2013年），但只有在（Kalloniatis等人，2020a）中通过概括MacKay（MacKay，2009年）的混合部队模型提出了一个具有明确网络结构的模型。在这里，网络优化形成了对战争机动理论中的概念识别。

在本文中，我们使用Kuramoto-Sakaguchi（Sakaguchi & Kuramoto，1986）的相位振荡器模型（建立在（Kuramoto，1984）的基础上）将C2引入（Kalloniatis等人，2020a）的表述中，从而在一个数学模型中统一了三个关键的作战功能：C2、机动和火力。对于一般网络，如（Acebr´on等人，2005）、（Arenas等人，2008）、（D¨orfler和Bullo，2014）和（Rodrigues等人，2016）开发的模型是

对于C2的应用（Kalloniatis等人，2020b），阶段代表单个代理的决策周期，自然频率代表代理的决策速度，耦合强度代表代理之间关系的紧密程度（或对决策状态变化的反应能力），网络代表正式和非正式的组织C2结构，挫败代表代理寻求与其他代理相比领先多少。公式（2）的相同框架可以扩展到两个（或更多（Zuparic等人，2021））相互竞争的部队或种群。这里用数学方法量化的两个要素，作为决策和组织的定性属性被很好地记录下来：认知心理学的感知-行动循环（Neisser，1976）或军事和商业战略的观察-判断-行动（OODA）循环中个人决策的周期性（Osinga，2006）；以及（Weick，1976）、（Perrow，2011）和（Hollenbeck & Spitzmueller，2012）阐述的组织中松紧耦合的作用。因此，该模型将组织理论中长期阐述的观点纳入了一个动态的数学模型。

为了更具体地说明这些想法，在我们引入的变量方面，考虑θi的前N个分量代表蓝方C2系统或网络中单个蓝方成员的OODA循环的连续版本中的决策状态。剩下的M个分量代表红方代理在他们自己相应的C2系统中的（OODA）决策状态。根据博伊德思想，蓝方和红方中的每一方都将寻求在对方之前稳定其决策状态，φi>φj，其中i，j可能代表蓝方或红方。因此，每一方的目标是比对方提前锁定阶段。蓝方相对于红方为ΦBR，红方相对于蓝方为ΦRB；为了简单起见，我们在每一组中，蓝方或红方的挫折值都是同质的。这些挫折值代表每一方的目标状态。他们是否实现了这一目标，取决于公式2所代表的动态，受制于他们的耦合、他们的连通性和他们个体的快速决策能力。

到目前为止，提到的 "决策"都是抽象的。在本文中，我们将其与C2在军事力量中要完成的任务联系起来。因此，我们建立了这样的模型：如果蓝方或红方的一个阶段θi领先于另一个阶段θj，他们将在兰彻斯特动态中获得优势。因此，我们提出了一个数学模型，使用多层网络表述，自然地统一了战斗、机动和C2作战功能（Boccaletti等人，2014）。该模型比（McLemore等人，2016）另一种基于方程的当代方法更紧凑，注意到他们在空间上嵌入了部队元素，并省略了C2。

对于同类兵力，我们的统一模型可以简化为全局形式，我们开始用它来说明结构，并以Kuramoto-Sakaguchi模型（Kalloniatis & Zuparic, 2016）的经验为基础，建立一个用例。虽然无法解决，但全局模型允许相当大的降维和洞察力。当兵力不均匀性较高时，全局模型的局限性较大，但全局模型展示了适应性动态，其中一种力量，例如蓝方，必须改变其资源分配，以适应更强大的红方力量。最后，通过一个虚构的复杂网络，我们说明了完整的模型是如何在经典的运筹学意义上使用的，以研究火力或C2系统投资之间的权衡。

在下文中，我们通过展示C2和战斗动力学如何在一个统一的Lanchester-Kuramoto-Sakaguchi模型中结合起来来介绍该模型的原理。我们只研究这个模型，因为它建立了一个可以应用于完整模型的直觉和近似方案。然后，我们制定了完全网络化的Lanchester-Kuramoto-Sakaguchi模型，并考虑了它的前两个用例，接着是一个复杂的网络，以显示网络化模型在作战研究中的效用。我们得出结论并讨论了未来的发展。进一步的分析计算细节和对一个用例的研究被归入附录中。