CNN如何剪枝？A*STAR最新《深度卷积神经网络结构化剪枝》综述，22页pdf阐述深度CNN结构化剪枝的最新进展

深度卷积神经网络(CNN)的卓越性能通常归因于其更深和更广泛的架构，这可能伴随着巨大的计算成本。因此，修剪神经网络引起了人们的兴趣，因为它有效地降低了存储和计算成本。与导致非结构化模型的权重剪枝相比，结构化剪枝通过产生对硬件实现友好的模型来提供现实加速的好处。结构化剪枝的特殊要求导致了许多新挑战的发现和创新解决方案的发展。**本文综述了深度CNN结构化剪枝的最新进展。总结并比较了最先进的结构化剪枝技术，包括过滤器排序方法、正则化方法、动态执行、神经架构搜索、ticket 假设以及剪枝的应用。**在讨论结构化剪枝算法时，简要介绍非结构化剪枝算法，以强调它们的区别。对结构化剪枝领域的潜在研究机会提供了见解。有关神经网络剪枝的论文列表可以在https://github.com/he-y/Awesome-Pruning上找到。

https://www.zhuanzhi.ai/paper/db65acc2c4f29634b8b2ee50c0fc1287

1. 引言

深度卷积神经网络(CNN)在广泛的应用中表现出了卓越的性能，包括图像分类[1]、目标检测[2]和图像分割[3]等。许多CNN结构被提出，包括AlexNet [4]， VGGNet [5]， inception [6]， ResNet[7]和DenseNet[8]。这些架构包含数百万个参数，需要巨大的计算能力，使得在资源有限的硬件上部署具有挑战性。模型压缩是该问题的一种解决方案，旨在减少参数数量、计算成本和内存消耗。因此，它的研究变得越来越重要。 **为了生成更高效的模型，模型压缩技术被提出，包括剪枝[9]、量化[10]、分解[11]和知识蒸馏[12]。**术语“剪枝”指的是删除网络的组件，以产生用于加速和压缩的稀疏模型。剪枝的目的是在不显著影响模型性能的情况下最小化参数的数量。大多数关于剪枝的研究都是在用于图像分类任务的CNN上进行的，这是其他计算机视觉任务的基础。剪枝可分为非结构化[9]和结构化剪枝[13]。非结构化剪枝删除神经网络的连接(权重)，导致非结构化稀疏性。非结构化剪枝通常会导致高压缩率，但需要特定的硬件或库支持以实现实际的加速。结构化剪枝删除了神经网络的整个滤波器，并可以利用基本线性代数子程序(BLAS)库等高效库的优势，用标准硬件实现实际的加速和压缩。在transformer[14]时代，从结构化剪枝的角度重新审视cnn的属性是有意义的。最近，将CNN的架构设计纳入Transformer模型[15]，[16]，[17]，[18]，[19]的趋势越来越大。尽管transformer中的自注意力[20]在计算序列表示方面是有效的，但由于transformer缺乏归纳偏差[17]，[21]，[22]，仍然需要大量的训练数据。相比之下，cnn的结构在权重上实施两个关键的归纳偏差:局部性和权重共享，以提高学习算法的泛化性，并且独立于数据[17]。本综述提供了对CNN的更好理解，并为未来有效设计架构提供了提示。

**本文关注结构化剪枝。现有压缩研究综述如表1所示。**一些综述涵盖了正交领域，包括量化[23]、知识蒸馏[24]和神经架构搜索[25]。一些调研[26]提供了更广泛的概述。虽然一些研究侧重于剪枝，但它们更多地关注非结构化剪枝，并且覆盖了少量结构化剪枝的研究。[27]、[28]、[29]、[30]、[31]、[32]、[33]的结构化剪枝论文引用数分别为1、11、15、55、38、10、20篇。本文提供了一个更全面的调研，其中有200多篇结构化剪枝论文。

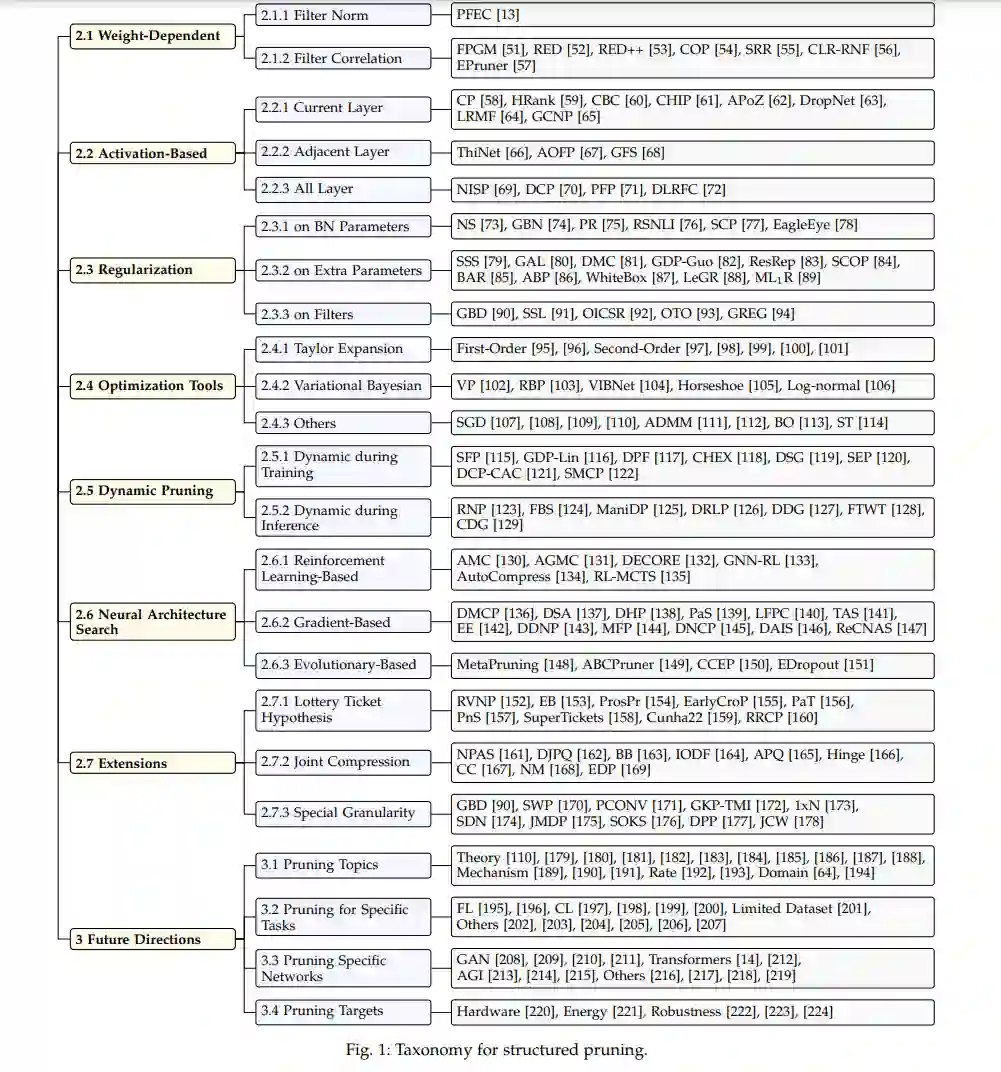
**调研安排如下:在分类法中(图1)，将结构化剪枝方法分为不同的类别。**第2节的每一小节对应于一类结构化剪枝方法。大多数方法首先以非结构化的方式开发，然后扩展以满足结构约束。尽管一些研究涵盖了多个类别，但我们将它们放在为本调查服务的最合适的类别中。第三部分介绍了一些潜在的和有希望的未来发展方向。由于篇幅限制，仅对最具代表性的研究进行详细讨论。

2. 方法

Weight-Dependent

权重依赖准则根据滤波器的权重来评估滤波器的重要性。与基于激活的方法相比，权重依赖的方法不涉及输入数据。因此，权重依赖方法被认为是直接的，需要较低的计算成本权重依赖准则有两个子类:滤波器范数和滤波器相关性。计算一个滤波器的范数独立于其他滤波器的范数，而计算滤波器相关性涉及多个滤波器。 Activation-Based

激活图是输入数据和滤波器的卷积结果(等式1)。除了使用滤波器的权重外，激活图可以用于滤波器修剪。激活通道剪枝是过滤器剪枝的另一个名称，因为删除激活图的通道等同于删除过滤器。除了当前层的效果外，过滤器修剪还通过特征图影响下一层的过滤器。为了评估第l层中的滤波器，我们可以利用以下激活图上的信息:1)当前层-通道重要性可以通过使用重建误差[58]、激活图[59]的分解、通道独立性的利用[61]和后激活[62]，[63]来评估;2)相邻层-冗余通道可以通过利用当前层和下一层之间的依赖关系来有效识别[66]，[67]。此外，还可以利用前一层的激活图来指导剪枝决策[123]，[124];3)所有层-通过最小化最终响应层的构造误差[69]并考虑所有层的区分能力[70]，可以评估去除滤波器的整体效果。 正则化

正则化可以通过添加不同的稀疏度正则化器Rs(·)来学习结构化稀疏网络。如果网络包含批量归一化层，则稀疏正则化器可应用于BN参数。为了实现结构化稀疏，使用BN参数来指示通道或滤波器等结构的剪枝决策。引入了作为可学习门工作的额外参数来指导修剪。有了这些额外的参数，网络不再需要批量规范化层。稀疏正则化器也可以直接应用于滤波器。Group Lasso正则化通常用于以结构化的方式稀疏化滤波器。

Optimization Tools

动态修剪

动态剪枝可以在训练和推理过程中进行。训练过程中的动态旨在通过在训练过程中保持动态修剪掩码来保持模型的代表能力。它也被称为软剪枝，以确保不当的剪枝决策在以后可以恢复。另一方面，硬修剪永久地消除了固定掩码的权重。推理过程中的动态表示网络根据不同的输入样本动态修剪。例如，与复杂图像相比，包含明确目标的简单图像需要更少的模型容量[108]。因此，动态推理提供了更好的资源准确性权衡。

神经架构搜索

由于人工确定逐层剪枝率等剪枝相关超参数非常繁琐，因此提出了神经架构搜索(NAS)[25]来自动寻找剪枝结构。在综述NAS[25]方法的基础上，将NAS剪枝分为3种方法。NAS可以建模为:1)强化学习(RL)问题，RL代理通过搜索动作空间(如剪枝率)来找到稀疏的子网络。2)基于梯度的方法，通过修改梯度更新规则，使稀疏约束的优化问题对权重可微。3)演化方法，采用演化算法对稀疏子网络进行探索和搜索。

Extensions