机器人正逐渐从工业和实验室进入我们的日常生活。无论是作为伴侣、教师、接待员、清洁工,还是满足其他需求,这些机器人都旨在提高我们的生活质量。然而,机器人的自主决策能力仍然是机器人技术面临的主要挑战。为了提高机器人的自主性,一方面,研究人员倾向于根据不同的标准对协作进行分类,以收集人机协作之间的共性。这样做的目的是检测机器人在执行各种任务时必须能够完成的相似步骤。另一方面,其他作品则侧重于增强建立人机协作所需的一个或多个领域。要实现人机协作,机器人必须完成四个标准步骤:感知、决策、运动执行和评估。
本论文旨在通过改进机器人的决策过程来优化人机协作性能。我们根据不同的可变性能指标来评估协作性能。因此,优化协作的目的是使人类受益,例如更快地完成任务或减少人类智能体的工作量。然而,未优化的协作将不会给人类带来任何益处,或者相反,即使最终完成了任务,也会给人类带来麻烦,如减慢人类的速度或使人类负担过重。
我们首先开发了一个优化机器人决策过程的全局框架。我们将这一框架应用于非直观的装配任务,即需要进行复杂的认知处理,以找到拟议装配游戏中每个部件的正确位置。我们希望提高人机协作团队完成任务的时间,而无需提高其物理能力(即感知、轨迹规划或低级控制)。我们提出的框架可在考虑不同性能指标的同时改善人机协作。这些指标的考虑与人类智能体的行为无关。
然后,我们将这一框架应用于第二个更复杂的应用(即软物体变形),该应用需要通过改进低级控制来提高机器人的操纵灵活性。事实上,我们将考虑第二种应用,这种应用要求提高机器人的操纵灵活性,以最大限度地优化协作性能。人机协作团队必须共同操纵软物体,使其达到所需的形状。协作团队可以使用深度强化学习方法来实现这一应用。我们的想法是在仿真中训练智能体(单臂机器人或双臂机器人),并通过用人类智能体替换第二机械臂进行实际测试。
关键词 人机协作 决策 博弈论 强化学习
通过改变性能指标优化人机协作决策过程的总体框架
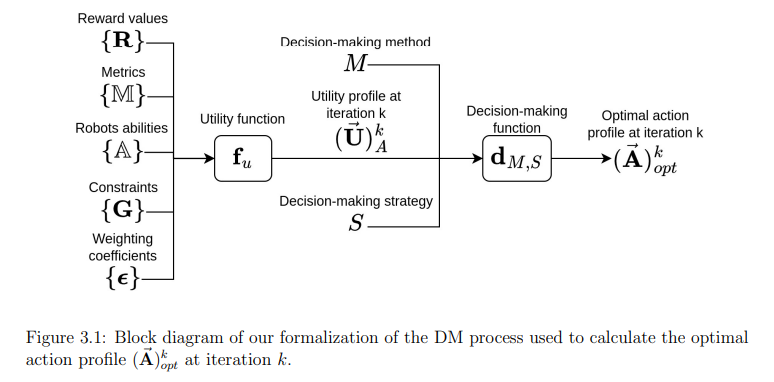
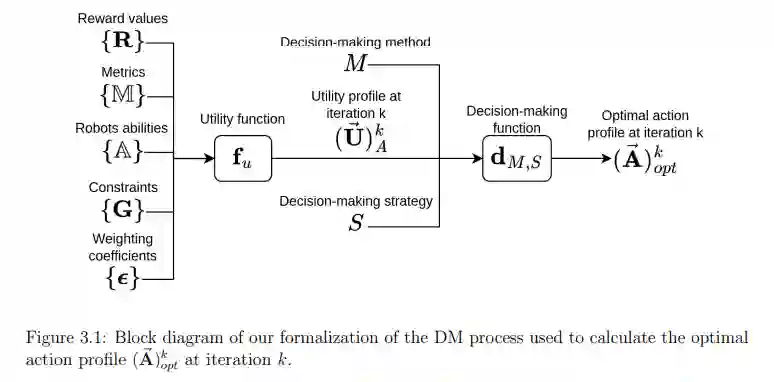
前面内容介绍了人机协作(HRC)中使用的决策(DM)方法、DM策略和奖励函数(或效用函数)。在本章中,我们将介绍在人机协作背景下的新DM框架。最先进的技术将人机交互视为一个优化问题,其中的效用函数(博弈论中使用的名称),也称为强化学习中的奖励函数,被定义为无论交互执行得如何,都要完成任务。当考虑性能指标时,它们不能在同一框架内轻易改变。
相比之下,我们的DM框架可以很容易地处理从一个案例场景到另一个案例场景的性能指标变化。我们的方法将HRC视为一个约束优化问题,其中效用函数(或奖励函数)分为三个主要部分:
-
一组评估协作绩效的奖励。这是改变性能指标时唯一需要修改的部分。它提供了对交互方式的控制,同时也保证了机器人的行动能够实时适应人类的行动。
-
一组定义如何完成任务的约束条件。
-
重新组合机器人物理能力的集合。
因此,可以设计效用函数(或奖励函数)来改善机器人的操纵灵活性。在本章开始,我们将介绍建立这样一个框架的动机和优势。然后,我们将我们的工作与最先进的技术进行比较。最后,我们将详细解释我们的形式化方法。
动机
如今,HRC已成为机器人领域中一个快速增长的领域。HRC旨在使人类的日常任务变得更加容易。它基于人类和机器人之间的信息交流,共享一个共同的环境,以队友的身份完成一项任务,实现共同的目标[28]。HRC应用可为人类带来社会和/或物理益处[11]。
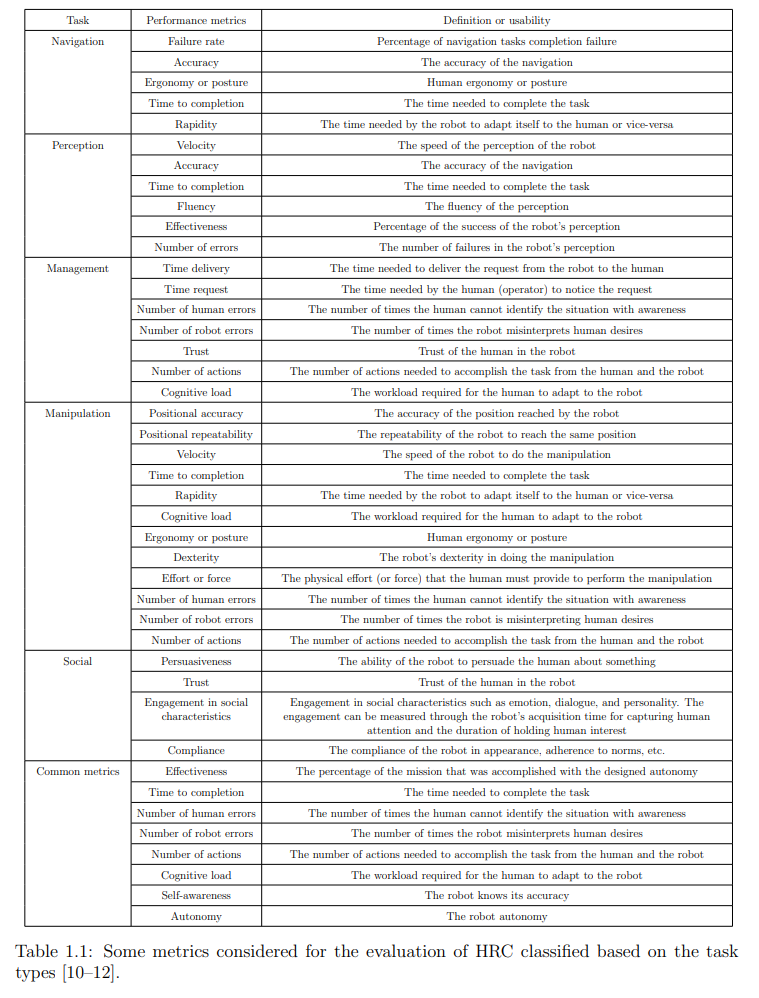
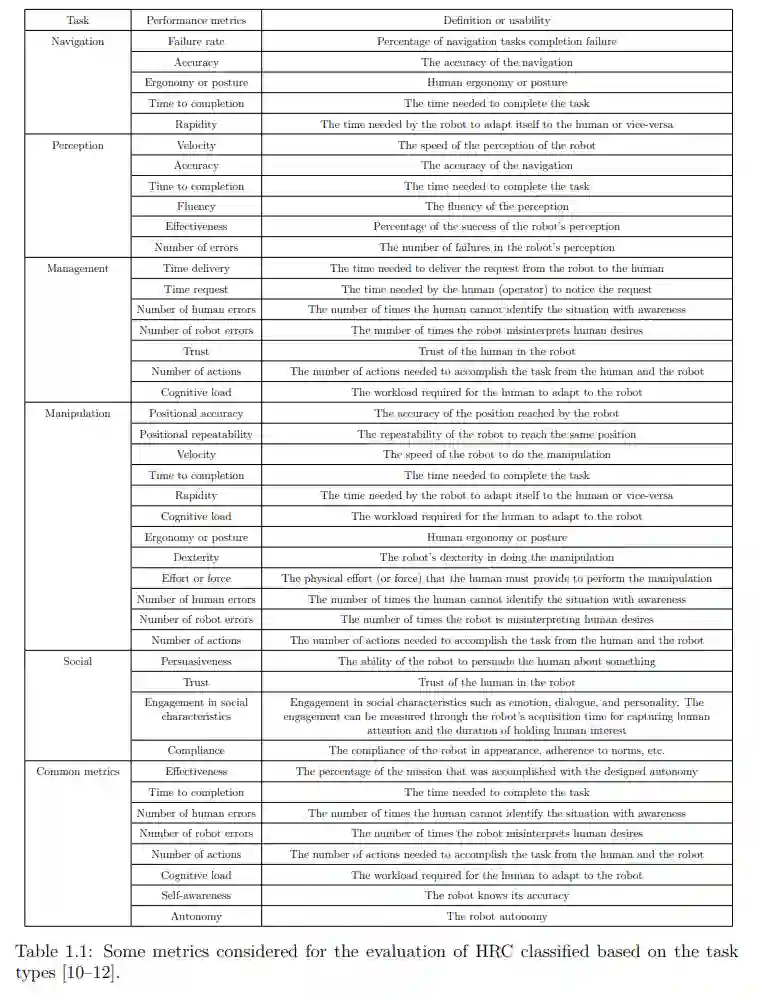
如第2章所述,机器人能够在不同情况下适应人类,这要归功于其DM过程,计算机科学中通常使用带有策略和效用函数的DM方法对该过程进行建模[42]。DM方法对整个情境(包括环境、行动、智能体、任务限制等)进行建模。策略定义了根据奖励值选择行动的政策。效用函数(即奖赏函数)通过赋予每个行动以奖赏来评估每个行动。如第2.3节所示,通过考虑性能指标(参见表1.1)来实现奖励函数,是提高HRC性能的一种可能性。
在本章中,我们将根据一些可改变的性能指标对人类智能体的影响,对机器人与人类之间的协作进行优化和定量评估。因此,优化的协作旨在为人类带来益处,例如更快地完成任务或减少人类智能体的工作量。然而,未优化的协作将不会给人类带来任何好处,或者相反,即使最终完成了任务,也会给人类带来麻烦,如减慢人类的速度或使其负担过重。本章的主要贡献在于,所提出的框架可根据一些可变指标,优化一个或多个人类与一个或多个机器人之间的协作性能。与以往的工作不同,我们的框架允许我们轻松地改变性能指标,而无需改变整个任务的形式化方式,因为我们在效用函数中隔离了指标的影响。
这一贡献的益处在于提高了协作性能,并有可能改善或不改善机器人的操纵灵活性。这在相关的实际案例中非常重要,例如,在使用社交机器人时,这些机器人有很大的局限性(例如,动作迟缓和/或灵巧性降低)[27],而大幅提高其能力并不容易,甚至不可能。因此,我们的工作提供了一个有趣的解决方案,以提高此类受限机器人的协作性能。
我们的框架采用最先进的DM流程,由DM方法、策略和效用函数组成。我们将效用函数(或奖励函数)分为三个主要部分:根据一个或多个性能指标,通过奖励来评估协作性能;任务完成度,由于我们只处理可实现的任务,因此将其视为约束条件;以及重新组合机器人物理能力的集合。在下面两节中,我们将简要回顾文献中如何使用效用函数,并提及我们在这方面的贡献。
效用函数或奖励函数
正如第二章中提到的,效用是由效用函数(或报酬函数)计算出来的报酬,用来表示一个行动的价值。通过这些效用,DM策略可以选择正确的行动。之前的一些文献只考虑了效用函数中的任务完成情况(而没有考虑性能指标),因为他们的重点是复杂任务的完成情况。例如,在文献[17]中,一个人机协作团队抬着一张桌子从一个房间移动到另一个房间。目标是通过让人类也适应机器人来确保代理之间的相互适应。在这类工作中,没有考虑表1.1中的任何性能指标。
较近期的作品包含了性能指标(见表1.1)。不过,他们认为,如果不对框架进行重大修改,这些指标是无法改变的。一个相关的例子是[156],通过改变任务分配,作者使机器人遵守装配过程的实时持续时间,同时按照必要的顺序装配零件。在这种情况下,他们只考虑了一个指标(完成时间),因为遵守零件装配顺序是完成任务的一个约束条件。然而,使用该框架,该时间指标不能被其他指标(如努力或速度)取代。
贡献
与目前工作中使用的效用函数不同,我们考虑的是可变的、不受限制的性能指标(见表1.1),这些性能指标通常无论人类行为如何都会被优化。总结我们的贡献,我们提出的框架允许我们
-
从一个场景到另一个场景,轻松地改变性能指标,而不需要改变我们形式化中的任何东西,除了效用函数中与指标相关的部分,以及
-
由于我们将奖励函数中的这一部分分离出来,因此可以在提高或不提高机器人操纵灵活性的情况下提高协作性能。
在下一节中,我们将定义问题的形式化并提出效用函数,该函数优化了性能指标,并以完成任务为目标作为约束条件。
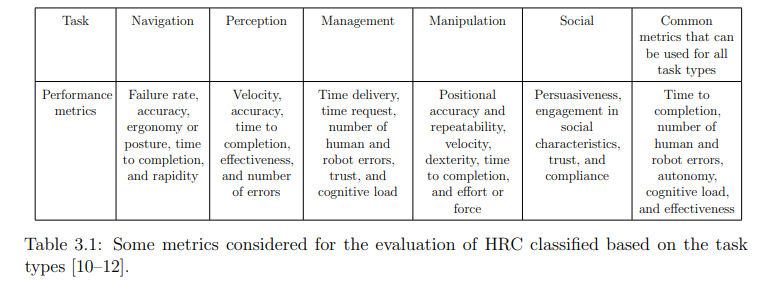
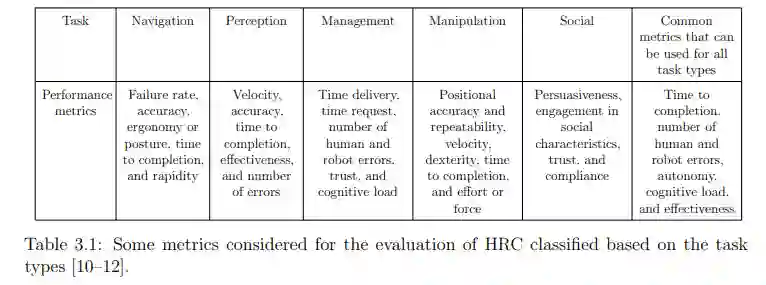
性能指标
只要某项指标可以用数学方法表述,或者至少可以在任务执行过程中进行测量,并作为计算任务奖励的条件,就可以通过性能指标{M}在选择行动时加以考虑。表 3.1 列出了我们可以考虑的一些性能指标。表3.1是第一章中表1.1的简化版。