Cristian Bodnar，微软研究院AI4Science团队的高级研究员，在那里从事深度学习和偏微分方程(PDEs)的交叉研究。在机器学习方面，研究涵盖了一系列主题，如几何和拓扑深度学习，图神经网络和神经微分方程。

拓扑深度学习

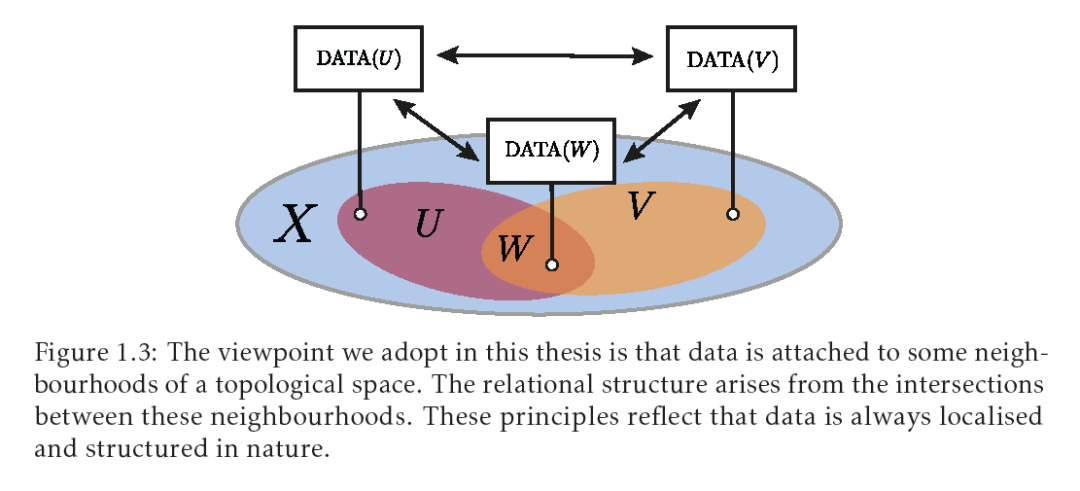
数据所处的空间类型——图、网格、格子、流形——正变得越来越多样化和异质化。因此，将不同领域间的思想、模型和理论结果进行翻译变得越来越具有挑战性。尽管如此，两个基本原则统一了所有这些设置。第一个原则是数据是局部的，意味着数据与基础空间的某些区域关联。第二个原则是数据具有关系性，这种关系结构反映了空间各区域的重叠方式。使用代数拓扑学对这些公理进行形式化是自然的。所讨论的“空间”是一个拓扑空间——一个具有邻域结构的集合——而附着在其邻域上的数据是代数对象，如向量空间。由于图形、流形以及之间的所有东西都是拓扑空间，我们采用这种数学视角来在领域之间平滑过渡，提高对现有模型的理论理解，以及设计新的模型，包括用于尚未在机器学习中探索的空间。在此视角指导下，本工作介绍了拓扑深度学习，这是一个研究在拓扑空间上粘贴数据的（深度）模型进行推断的研究计划。

这篇论文包括四项研究工作，扩展了上述的研究方向。第一项研究提出了信息传递单纯网络（Message Passing Simplicial Networks，MPSNs），这是一种在单纯复杂体上运行的模型家族，单纯复杂体是代数拓扑学中图的高维泛化。我们研究这些模型必须满足的对称性，描述它们行为的拓扑不变量，以及它们如何学习基于离散微分形式的表示。

第二项研究将这种泛化进一步推广到单元复杂体，这是一个空间类别，也包括了单纯复杂体。我们展示了他们的额外灵活性对分子应用的好处，其中得出的模型在分子属性预测任务上超越了先前的艺术。

第三项工作提出了一个构建图粗化（又名池化）操作符的通用拓扑框架，该框架自然地推广了计算机视觉中现有的池化方法。我们展示了这个框架可以用于构建基于图的分层模型和可视化有属性的图。

最后，最后一项工作引入了一个基于鞘理论的新视角来看待图模型，鞘理论是代数拓扑学的一个子领域。鞘是一种数学数据结构，它自然地存储附着在拓扑空间及其关系结构上的数据，并忠实地实现了拓扑深度学习的公理原则。我们展示了图上的鞘结构与信息传递图模型的渐近行为紧密相关，并利用这些连接设计新的基于鞘的卷积架构。我们证明这些模型可以应对过度平滑和异质图的挑战，这些挑战影响了许多现有的图模型。

总的来说，这篇论文为结构化数据的深度学习引入了一种新的拓扑视角，其影响建立了许多与代数拓扑的新联系。

引言

随着时间的推移，机器学习（ML）模型可以处理的空间类型不断演变。2010年代初期，深度学习模型的崛起得益于对欧氏空间（如图像、视频、文本和音频）支持的数据。这一深度学习的首次成功自然而然地引发了在非欧氏领域（如图、流形、网格和向量束）上运行的模型的出现。在很大程度上，这第二代模型是由这些空间存在的无数应用（特别是在生命科学中）所驱动。这个领域的许多里程碑包括事实上解决了蛋白质折叠问题（Jumper等人，2021），证明了纯数学中的旧猜想（Davies等人，2021），以及改进了Google地图上的ETA预测（Derrow-Pinion等人，2021）。

随着空间和生活在其中的数据家族变得越来越多样化，从基本原则出发的统一的数学观点越来越必要。然而，这个方向的努力受到这些领域的异质性的阻碍，它们范围从离散组合空间（如图）到高度结构化和连续的空间（如黎曼流形）。到目前为止，统一的尝试完全是几何性质的。Bronstein等人（2017）的“几何深度学习”（GDL）论文在推广几何视角方面具有特别的影响力，它提供了如何将深度学习模型从网格状领域泛化到非欧氏空间的概述，这使用了微分几何的思想。

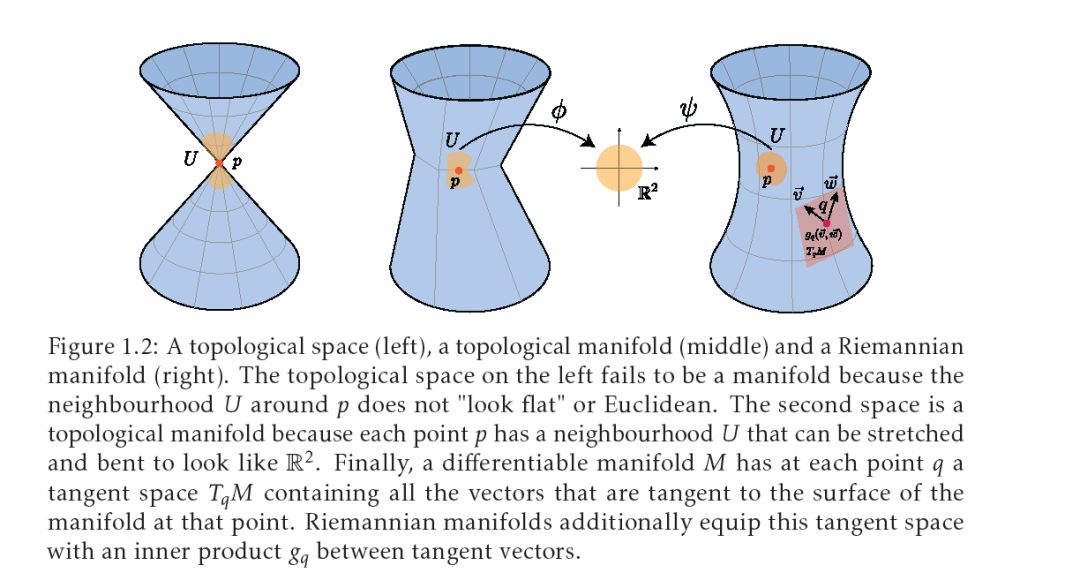
然而，微分几何只是数学空间故事的一部分，整个结构阶梯（图1.1）描述了这个故事。在其基础上，我们发现了集合，它只是一组元素的集合。首先，集合可以赋予拓扑结构，这增加了一个点周围的邻域的概念。由一组和邻域结构形成的结果对象称为拓扑空间。接下来，一些拓扑空间在每个点周围的邻域内“看起来像”欧氏空间。这些被称为拓扑流形。在这个阶段，我们可以进一步为拓扑流形配备一个可微（光滑）结构，这使我们能够将微积分泛化到这些非欧氏空间。最后，对于我们的目的，结构阶梯在黎曼流形上达到顶点，黎曼流形是也配备有切向量内积的可微流形。在这个阶梯的顶部，我们现在有了定义非欧氏设置中熟悉的几何概念（如长度、角度、面积或曲率）的所需结构（图1.2）。

由于并非所有的空间都配备了或可以配备这些结构层，自然而然地采用我们可以对任何集合施加的最通用类型的结构允许的视角：拓扑结构。这篇论文依赖于一个基本观点，即数据生活在一个拓扑空间的邻域中，数据有一个由各种邻域的重叠方式引导的关系结构。由于任何空间，无论是离散的还是连续的，都是一个拓扑空间，所以可以轻易地在各种空间之间过渡，同时始终有代数拓扑的强大工具可供使用。如下一章将看到的，最初激发了“几何深度学习”一词的“非欧氏空间”的概念，可以在没有任何几何结构的情况下被拓扑解释。许多非欧氏空间，如图，这是本论文主要关心的空间之一，不鼓励几何观点。与机器学习中的其他离散结构（例如网格）不同，图甚至不是拓扑流形（一般情况下）。因此，通常无法将在序列、图像、网格或流形上开发的模型适应到图表，因为（离散）微分几何的工具不可能立即无摩擦地应用。图并不是唯一的例子，几乎整篇论文都致力于几何上“行为不良”的空间（即非流形），就像图1.2左侧所示的那样。

近年来，Felix Klein对几何的一般性概念，视为理解对称群不变性的理解，已经对深度学习社区产生了深远影响。这个视角已经成为GDL的基础，它被描述为“机器学习的埃朗根程序”（Bronstein等人，2021）。类似于Klein的Erlangen程序（Klein，1893），该程序根据他们必须满足的对称性对他的时代出现的各种几何进行分类，GDL已经成为试图根据他们必须满足的对称性对深度学习模型进行分类的鼓舞人心的尝试。这个观点与我们在这篇论文中采用的拓扑观点并不遥远。在《形式分析》（Poincaré，1895）中，这个标志着拓扑学诞生的作品中，Poincaré定义了拓扑学为一种空间的光滑变形群的研究，因此，那些在这样的变形下保持不变的性质（Bartocci，2013；McCleary，2013）。因此，在Poincaré的观点中，拓扑学是Klein几何的一个分支。尽管这些概念有重叠，但变形群与所谓的李群（即也是可微流形的群）非常不同，后者描述了Klein几何中的空间的对称性以及更一般的机器学习应用。此外，设计对这样的变形不变的模型通常是不合理的，这些变形可以严重扭曲输入空间。相反，我们的目标是研究拓扑不变量如何自然地出现在应用于拓扑空间的深度学习模型中，以及他们如何利用它们。最后，尽管基于对称性的几何视点无疑是引人注目的，并且涵盖了图1.1中结构阶梯的所有级别，但它可能会掩盖所有这些数学层次的交互和内部工作。因此，我们在这篇论文中采用的拓扑方法可以提供一个与以前的几何尝试正交的新的基础性的领域描述。