利用概率学实现组合优化层，新研究构建Julia开源包InferOpt.jl

机器之心报道

机器之心编辑部

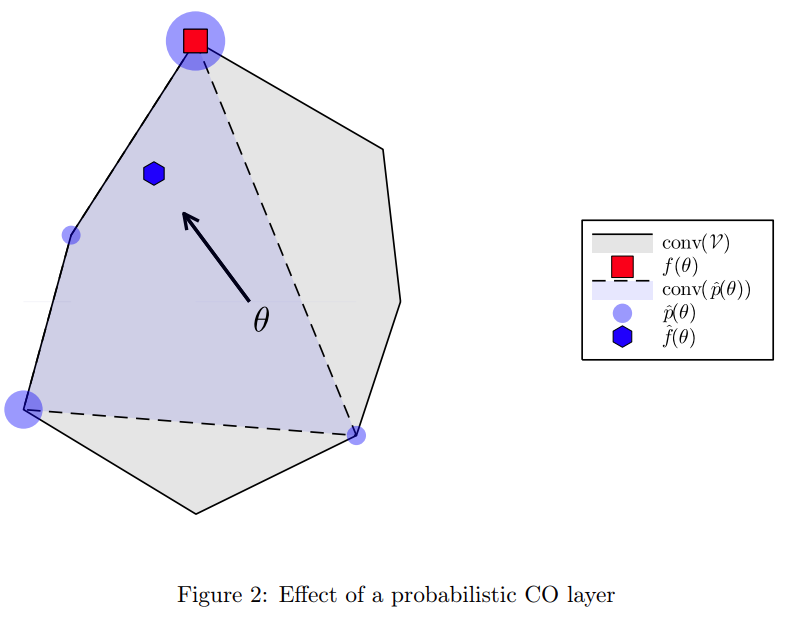
从概率学的角度实现 CO 层，有助于构建近似微分和结构化损失函数。

机器学习 (ML) 和组合优化 (CO) 是现代工业流程的两个重要组成部分。 ML 方法能从嘈杂的数据中提取有意义的信息，而 CO 可以在高维受限环境中做出决策。 在许多情况下，我们希望将这两种工具结合使用，例如从数据中生成预测，然后使用这些预测做出优化决策。 因此，混合 ML-CO pipeline 成为一个新兴的研究方向。

然而这里存在两个问题。首先，CO 问题的解通常表现为其目标参数的分段常函数，而 ML pipeline 通常使用随机梯度下降进行训练，因此斜率是非常关键的。其次，标准的 ML 损失在组合环境中效果不佳。

此外，组合优化层（CO 层）往往缺乏良好的实现。近日一项新研究从概率学的角度提出了实现 CO 层的方法，有助于近似微分和结构化损失的构建。

论文地址：https://arxiv.org/abs/2207.13513

基于这种思路，该研究提出了一个开源的 Julia 包——InferOpt.jl，它的功能包括：

• 允许将任何具有线性目标函数的 CO oracle 转换为可微层；
• 定义损失函数来训练包含可微层的 pipeline。

InferOpt.jl 开源包地址：https://github.com/axelparmentier/inferopt.jl

InferOpt.jl 适用于任意优化算法，并且与 Julia 的 ML 生态系统完全兼容。研究团队使用视频游戏的地图寻路问题来展示它的能力。

推理问题的关键是预测给定输入的输出，这需要了解每个 ML 层的参数。而学习问题旨在找到在推理过程中导致「良好」输出的参数。如下等式 (1) 所示，现有的「CO oracle」代表可以解决优化问题的算法，包括基于求解器和手工的算法。

而层的定义是指我们可以使用自动微分 (AD) 计算有意义的导数，但现有 CO oracle 很少与 AD 兼容，并且导数几乎处处为零，没有可利用的斜率信息。

因此，此前 CO oracle 还不是层，该研究的重点就是利用概率学的知识将其变成一个层。现代 ML 库提供了丰富的基本构建块，允许用户组装和训练复杂的 pipeline。该研究试图利用这些库来创建混合 ML-CO pipeline，并主要解决了两个问题：

• 将 CO oracle 转换为可用层；
• 找到合适的 ML 损失函数，避免忽略潜在的优化问题。

 

感兴趣的读者可以阅读论文原文，了解更多研究细节。

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com