经典算法与神经网络如何结合？德国康斯坦茨大学Felix Petersen《可微算法学习》博士论文，162页pdf

经典算法和神经网络等机器学习系统在日常生活中都很丰富。经典的计算机科学算法适合精确地执行精确定义的任务，例如在一个大图中找到最短路径，而神经网络允许从数据中学习，以预测更复杂的任务，如图像分类中最可能的答案，这不能简化为一个精确的算法。为了更好地利用这两个世界，本文探索了将这两个概念结合起来，从而得到更健壮、更好的性能、更可解释、更高效的计算和更高效的数据架构。本文提出了算法监督的概念，使神经网络能够从算法中学习或与算法结合。当将算法集成到神经体系结构时，重要的是算法是可微的，这样的体系结构可以端到端训练，梯度可以通过算法以有意义的方式传播回来。为了使算法具有可微性，本文提出了一种通过扰动变量和封闭逼近期望值来连续松弛算法的通用方法，即:，不需要采样。此外，本文还提出了可微算法，如可微排序网络、可微呈现器和可微逻辑门网络。最后，本文提出了用算法学习的其他训练策略。

https://www.zhuanzhi.ai/paper/8c415ddbac1f3d1c24e4bb5436caf786

Felix Petersen 研究兴趣是具有可微算法的机器学习。例如，我已经做了一个使算法可微的通用框架，并且也关注了可微排序和可微渲染。虽然通过传播分布来使算法可微分非常有趣，但我也喜欢通过神经网络传播分布，这可以提高不确定性估计、鲁棒性和公平性。

我在康斯坦茨大学的视觉计算小组(Oliver Deussen教授)工作，并与Christian Borgelt, Hilde Kuehne, Mikhail Yurochkin等人合作。

https://petersen.ai/

四千年前，埃及人发明了两个数字相乘的算法，这是[21]算法的最早记录。1843年，Ada Lovelace发布了第一个算法计算机程序，并设想了计算机在艺术和音乐等方面的现代应用，而当时这样的计算机甚至还没有制造出来[22,23]。一个世纪后的1943年，麦卡洛克和皮茨根据对大脑生物过程的观察，设计了第一个神经网络的数学模型。近十年来，基于人工神经网络的方法在研究中受到了广泛关注。这种复苏可以归因于硬件[25]、软件[26-29]、卷积网络[30,31]的发展以及深度学习在许多任务(如图像分类[32,33])上的优势。

如今，经典算法和神经网络等机器学习系统在日常生活中都很丰富。虽然经典的计算机科学算法适合精确执行精确的任务，如在一个大图中找到最短路径，但神经网络允许从数据中学习，以预测更复杂的任务(如图像分类)中最可能的答案，这不能简化为一个精确的算法。为了达到这两个世界的最佳效果，在这篇论文中，我们探索了将经典计算机科学算法和神经网络，或者更一般地说，机器学习相结合。这将导致更鲁棒、更好的性能、更可解释、更高效的计算和更高效的数据架构。文中提出了一种可证明正确的嵌入算法，实现了模型的鲁棒性。用一种快速算法代替神经网络的一部分，降低神经网络的计算复杂度，可以提高模型的计算性能。此外，在精确度方面，性能可以提高，因为有更小的潜在错误，并且领域知识支持网络。相应地，这些模型也可以更容易解释，因为算法的输入通常(根据定义)是可解释的。最后，由于算法监督是一种典型的弱监督学习，监督水平降低，模型的数据/标签效率更高。通常，神经网络使用随机梯度下降(SGD)或预处理SGD方法进行训练，如Adam优化器[34]。这些方法基于计算损失函数相对于模型参数的梯度(即导数)。这个梯度表示损失的最陡上升方向。由于最小化损失改进了模型，我们可以(在模型的参数空间中)沿着梯度相反的方向进行优化，即梯度下降。使用反向传播算法[35]可以有效地计算损失相对于模型参数的导数，在当今的深度学习框架[26,29]中，该算法被实现为向后模式自动微分。

基于梯度的学习要求所有涉及的操作都是可微分的; 然而，许多有趣的操作，如排序算法是不可微的。这是因为像if这样的条件语句是分段不变的，也就是说，它们的导数为0，除了在真和假之间的转换(即“跳转”)之外，它们的导数是未定义的。因此，使用(不可微分)算法进行基于梯度的学习通常是不可能的。因此，在这项工作中，我们专注于通过连续松弛使算法可微。连续松弛的基本思想是在算法中引入一定程度的不确定性，例如，它可以使if语句中的真和假平滑过渡，使算法完全可微。我们注意到，当超越反向传播时，例如，通过RESGRO损失，如第七章所介绍的，可微性和平滑性不是严格必要的，但仍然是可取的。我们还注意到，在这项工作中，将无梯度优化算法与基于梯度的神经网络学习结合在一起，可微分算法通常优于无梯度方法。

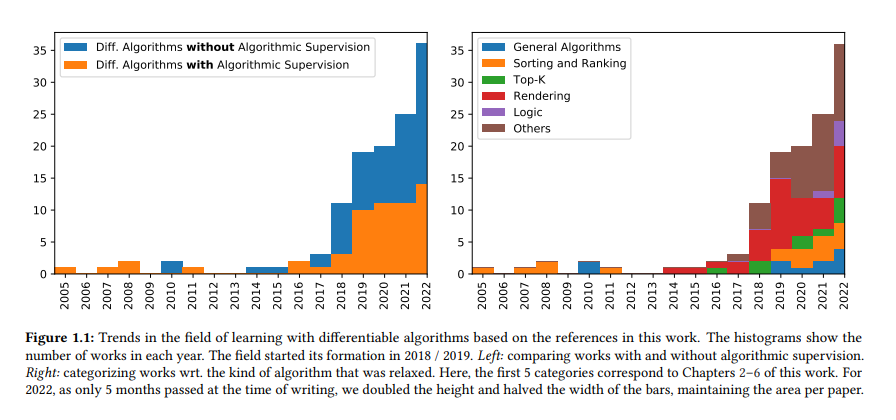
可微算法学习可以分为2个学科: I可微算法，即研究如何通过算法反向传播并获得有意义的梯度。I算法监督(Algorithmic Supervision)，将算法知识融入到神经网络模型的训练中。可微算法学习是机器学习中一个相对较新的领域。具体来说，除了一些个人早期的作品外，可微算法和算法监督领域在2018年取得了进展。我们已经在图1.1的调查直方图中可视化了这一点。在这里，我们将所有关于可微算法的相关工作分为应用算法监督的和不应用算法监督的(左)。进一步，我们将它们分类为wrt。他们提出或应用的可微算法。我们注意到，作者在2018年提出并开始了可微算法的研究，即在该领域形成之初。我们还注意到，该领域正在发展，最近才看到对现实问题的直接应用。

本论文共分为8章:各章按时间顺序依次展开，具体来说，第2章介绍了3-6章构建的核心思想和方法。第7章介绍了备选的优化方法，因此在很大程度上独立于第2 - 6章的时间流程，但建议从第2章和第3章中获取知识，以便深入理解应用程序。

第一章介绍了可微算法学习的核心思想，并涵盖了重要的相关工作和应用。

第二章详细介绍了可微算法和算法监督的一般方法。为此，这一章给出了可微算法的一般概述，并可以视为引言的延伸。接下来的章节以本章的思想为基础，每一章都更深入地讨论了一类特定的可微算法。

第三章研究了可微排序和排序方法，重点研究了可微排序网络。我们首先介绍可微排序方法，并通过仔细的理论分析，得出改进的可微排序算子。

第四章介绍了可微top-k方法，在概念上建立了可微排序和排序方法。特别地，我们引入了可微top-k网络，这是对top-k算子可微排序网络的改进。在可微top-k的基础上，我们提出了top-k分类学习，并在ImageNet分类任务上取得了优异的性能。

第五章介绍了可微呈现。我们介绍了可微渲染的各种方法，并提出了广义可微渲染器GenDR，它(至少近似地)包含了大多数现有的可微渲染器，还可以推广到新的可微渲染器。本章附有图书馆。

第六章提出了可微逻辑门网络，它是逻辑门网络的一种松弛，因此可以训练。这允许极快的推理速度，因为由此产生的逻辑门网络可以在普通硬件上本机执行，因为这种硬件首先在逻辑门上操作。这是一个可微分算法的例子，它可以被训练，并不一定与算法监督有关。

第七章讨论了备选的优化策略。具体来说，它讨论了分裂反向传播，一种基于正则化的通用两阶段优化算法，它允许使用不同于用于优化神经网络的优化器来优化算法损失。分裂反向传播还允许将神经网络本身分裂为多个部分，并可以扩展到多个分裂，然后所有的训练都可以端到端，即使子部分是用替代优化器训练的，甚至是不可微的。

在第八章，我们总结了本文的主要贡献，并讨论了未来的研究方向。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“D162” 就可以获取《经典算法与神经网络如何结合？德国康斯坦茨大学Felix Petersen《可微算法学习》博士论文，162页pdf》专知下载链接

                       

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取100000+AI(AI与军事、医药、公安等)主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取100000+AI主题知识资料