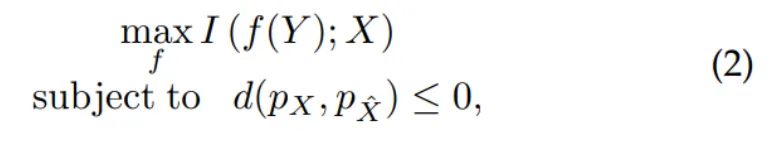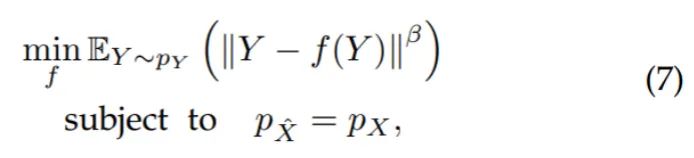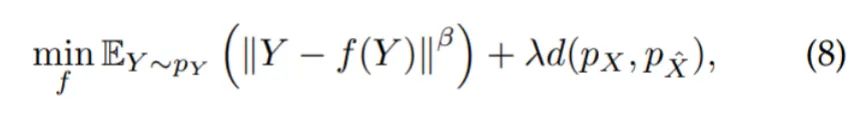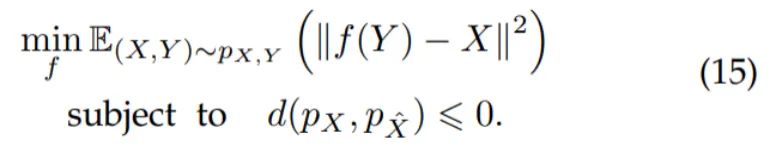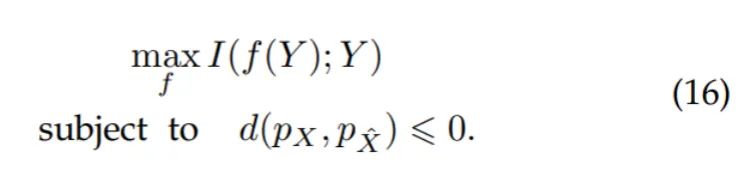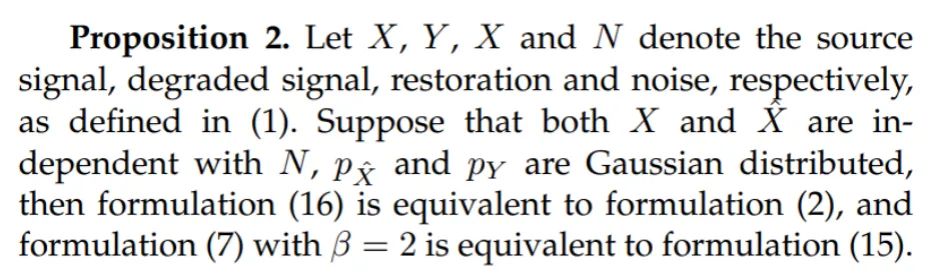【上海交大-TPAMI 2022】基于最优传输理论的无监督图像重建学习

作者丨王炜来源丨上海交通大学类脑智能应用与技术中心转载丨极市平台

导读 本项研究基于最优传输理论构建无监督重建学习的最优框架，证明了Wasserstein-1空间中最优传输准则的松弛求解不变性。在摄影图像、荧光显微镜图像、深度图像等多种实际数据上，新方法实现了远超现有无监督/自监督方法的性能，在重建感知质量上甚至优于SOTA有监督方法。

论文地址：https://ieeexplore.ieee.org/document/9763342 开源地址代码：https://github.com/wangweiSJTU/OTUR

图像重建是底层计算机视觉中的一个基本问题，对于后续的许多高层任务至关重要。在过去的几年里，随着卷积神经网络的发展和大量成对训练数据集的构建，图像重建任务取得了长足的进展。然而，在许多实际应用中，难以收集足够的干净图像进行监督学习，虽然可以使用合成数据进行代替，但真实数据与合成数据之间的差异将从根本上限制重建模型在真实场景上的性能。如图1所示，ToF深度相机采集的原始深度图像包含大量复杂噪声，如图中红色部分为无效值，同时真实场景的高质量3D成像难以获得。在此类复杂噪声的真实场景下，监督学习方法无法适用。

图1 真实原始ToF深度图像

近年来，自监督和无监督图像重建学习取得了很大进展。然而，现有的方法或多或少地依赖于对图像和退化模型的一些先验假设，这限制了它们在真实数据上的表现。如何在没有任何退化模型先验知识的情况下构造无监督重建学习的最优准则仍然是一个悬而未决的问题。为了回答这个问题，上海交通大学类脑智能应用技术研究中心团队最近提出了一种基于最优传输理论的无监督重建学习框架。其将图像重建视为从真实带噪分布到干净分布的一个传输问题，基于最优传输理论，在实现高感知质量重建的同时，可以最大限度地保留信号的信息。在多种仿真和真实场景下的实验表明，该方法在取得接近有监督学习方法的峰值信噪比的同时，可以获得更好的感知质量。

本项工作的主要贡献有：

1. 提出一种基于最优传输理论的无监督重建学习准则，在重建输出与干净自然样本具有相同分布的约束下，最小化输入和重建输出之间的传输成本。
2. 将该准则与理想有监督准则进行了对比分析，表明该准则在实现高感知质量重建的同时，能够最大程度地保留原始图像的信息。
3. 在实际训练实现中需要把该带约束的最优传输准则松弛为无约束的形式，以方便基于对抗训练进行学习。本文在理论上证明了：对于Wasserstein-1距离，该松弛不影响最有传输的最优解，即松弛后与原始准则具有相同的最优解。
4. 将新方法应用于多种去噪应用，包括不同仿真噪声下的合成图像，以及真实世界的手机摄影、显微镜、深度图像。结果表明，新方法在取得逼近有监督学习方法的失真度量（PSNR，SSIM）的同时，具有更好的重建感知质量。特别地，在去除带有复杂噪声的原始深度图像实验中，新方法表现出了非常大的优越性。

理论和方法介绍

理想的有监督学习准则

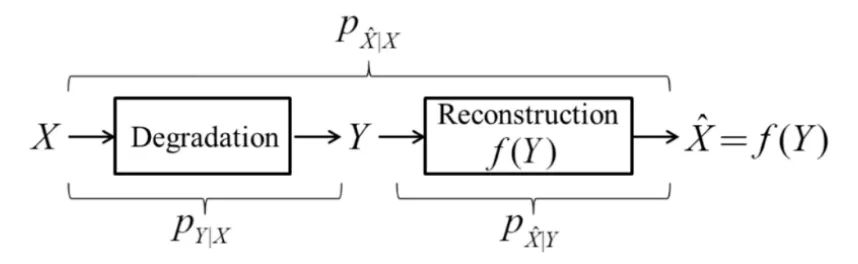
图像的退化和重建过程如图 3 所示，其中 为干净图像， 为退化后的图像， 为网络重 建后的图像， 为重建的网络模型。

图3 图像重建问题 对于去噪任务而言，退化模型可以表示为

其中 为噪声。该加性噪声模型会在之后的信息论相关分析中会用到，但本文所提方法并不假设噪声为加性模型。 一般来说，图像重建的理想目标有以下三个:

1. 噪声抑制：尽可能抑制 中的噪声；
2. 最大信息保留: 尽可能保留 中包含的原始信号的信息；
3. 高感知质量重建：在重建中实现高感知质量，图像感知质量是指从人的主观视觉判断重建图像看起来像干净自然图像的程度，根据现有研究，失真度量（如PSNR、SSIM）与感知质量之间存在一个权衡取舍，即提升感知质量会导致重建失真的上升。

因此有监督学习下图像重建的理想准则可以表示为：

其中 表示分布间的散度。该准则在约束重建图像 与干净图像 间分布相同的条件 下，最大化保留重建图像 和 之间的互信息。

基于最优传输理论的无监督图像去噪最优准则

最优传输问题旨在找到将一种质量分布转换为另一种质量分布的最有效传输映射，同时最小化传输成本，其在信号处理、图像处理和机器学习中有着广泛的应用。 假设 和 是 和 上的两组概率测度，设 是一个代价函数，衡量将 传输到 的代价。最优传输问题的目标就是寻找将 传输到 代价最小的传输映射。 其中传输映射(transport map)的定义如下：

Monge在1781年提出的最优传输问题定义如下：

本质上，图像重建问题可以视为一个最优传输问题，即寻找带噪图像分布到干净图像分布的最优传输函数。因此，提出无监督下的重建学习准则：

其中，可以发现问题(7)是上述最优传输问题的一种实现。 看似准则(7)违背直觉，因为它将重建目标推向了带噪输入，但是深入分析后会发现，该问题旨在寻找一个满足以下条件的重建映射 :

1. 高感知质量重建: 约束 ，确保重建图像 与干净样本 有相同的分布，因此可以保证生成图像具有良好的感知质量。
2. 最小传输成本：问题(7)中使用观测值 来确保重建的保真度，具有最小传输特性，之后会证明该特性使重建映射实现了对 中包含的 的信息的最大保留。

为了便于实现，我们将带约束问题(7)松弛为无约束的形式：

虽然进行了松弛，本文证明了：当 为 Wasserstein-1 距离，且 时，问题 和 有相同的最优解，具体定理如下:

该定理的具体证明过程可以在原论文中找到。

从信息论角度看所提出准则

这一部分，将从信息论角度出发，来证明所提出的准则(7)找到的重构映射 可以近似地最大限度保留 中包含的 的信息。 首先，(2)给出了理想的有监督学习准则，该准则在最大化 和 之间互信息的同时实现了感知重建。在实际应用中，除了某些简单的特定数据分布，互信息难以显式计算，因此 MSE 被广泛用作重建损失，其中有监督准则(2)的实现可以写成:

当 和 为高斯分布时， 等价于最大化 和 的互信息，因此当 时，所提出的无监督学习准则(7)可以视为高斯分布下无监督学习的信息论准则的特例。

同时我们证明了，当 和 与噪声无关， 和 均为高斯分布时，(16)则等价于(2)， 时(7)等价于(15)，即所提出无监督学习准则在特定条件下等价于监督学习准则。

具体证明过程请参考原论文。 需要注意的是，从马尔科夫链 可以得到不等式: ，此时 是 的上界。如果重建映射 能够完美地抑制噪声 (即 与 无关)，则可以通过最大化互信息 来最大限度地保留 中包含的 的信息。在大多数应用中，干净数据 与噪声 无关的假设是合理的。然而，重建 和噪声 之间独立的假设是不切实际的，因为不能保证观测 中的噪声分量被完全抑制。实际上，当去噪过程 能够在很大程度上抑制 中的噪声分量时， 和 之间的相关性将很弱。在这种情况下，无监督准则(16)可以被视为理想的有监督准则(2)的近似。

实验

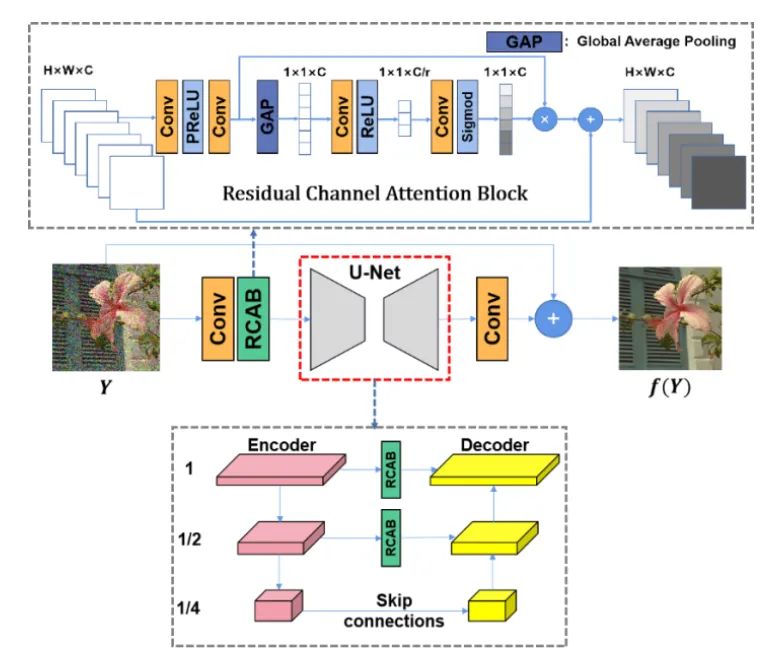
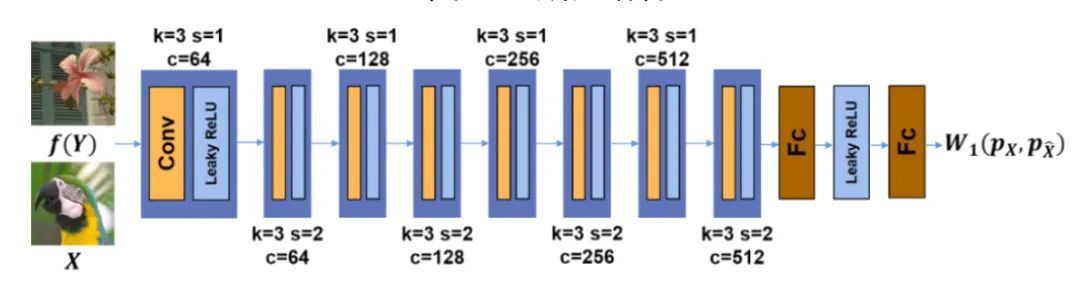
本节中使用WGAN-gp对所提出准则进行实现，其中生成器结构如图3所示，鉴别器结构如图4所示。其中生成器主体结构为U-Net架构，它由编码器中的两个下采样CNN层和解码器中的两个上采样CNN层组成。残差通道注意力模块（RCAB）被用于每个下采样和上采样层来增强网络的生成能力。我们在仿真RGB图像、仿真深度图像、真实显微镜图像、真实手机摄影图像、真实深度图像和真实原始深度图像上均进行了实验测试，并与当前最佳的一些监督学习、自监督和无监督学习方法进行了对比，此处因篇幅限制仅挑选部分进行展示，具体内容可参考原论文。 测试中使用了PSNR和SSIM作为失真度量指标，Perception Index (PI)和Learned Perceptual Image Patch Similarity (LPIPS)作为感知质量指标。

图3 生成器结构

图4 鉴别器结构

1.仿真噪声下RGB图像降噪

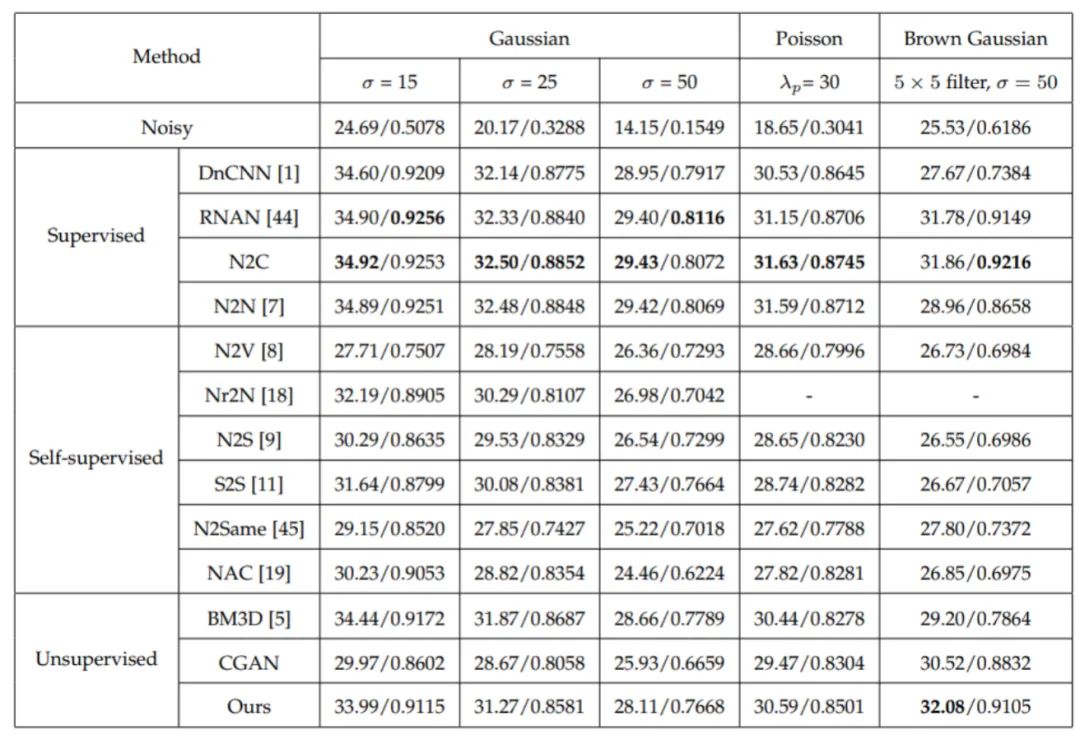
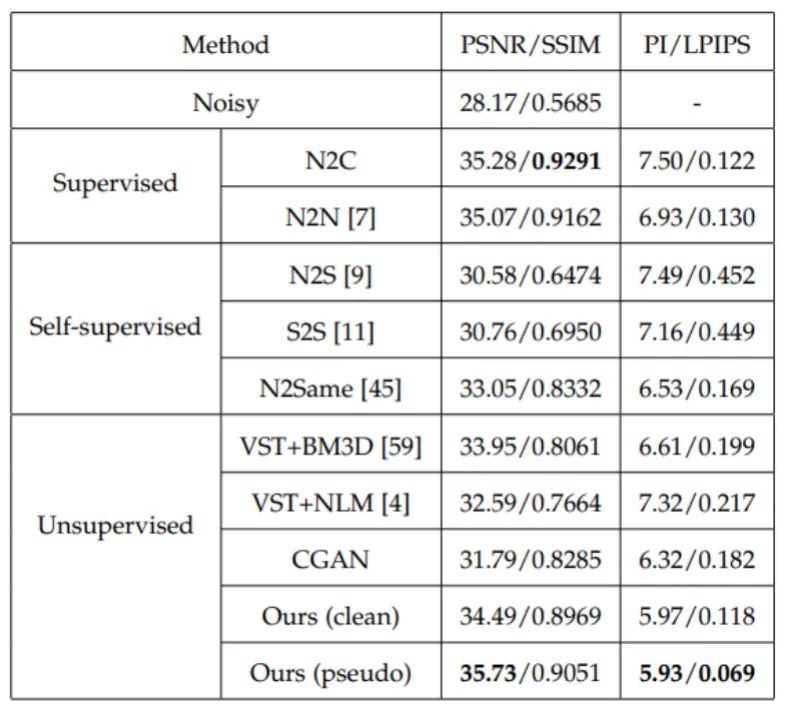
首先是仿真噪声去除实验，所测试的合成噪声类型包括加性高斯噪声、泊松噪声和布朗高斯噪声，其中布朗高斯噪声是使用一个核大小为5*5的高斯滤波器过滤标准差为50的高斯噪声得到的。使用了BSDS500作为训练数据集，KODAK24作为测试数据集，表1和表2分别为失真度量和感知质量测试结果，对于空间独立的高斯噪声和泊松噪声，所提出方法比监督学习方法PSNR低1dB左右，而在空间相关的布朗高斯噪声中，所提出方法取得了最佳的PSNR，此外在所有噪声中，所提出方法均获得了最佳的PI/LPIPS分数，这表明其可以得到最佳的感知质量。如图5所示，所提出方法比DnCNN、N2C、N2N、N2V和BM3D具有更好的感知质量，因为它保留了更多的细节信息。

表1 失真度量(PSNR/SSIM)测试结果

表2 感知质量(PI/LPIPS)测试结果

图5 不同仿真噪声下图像去噪的视觉比较，括号中为图像的PSNR/PI/LPIPS分数

2.真实显微镜图像

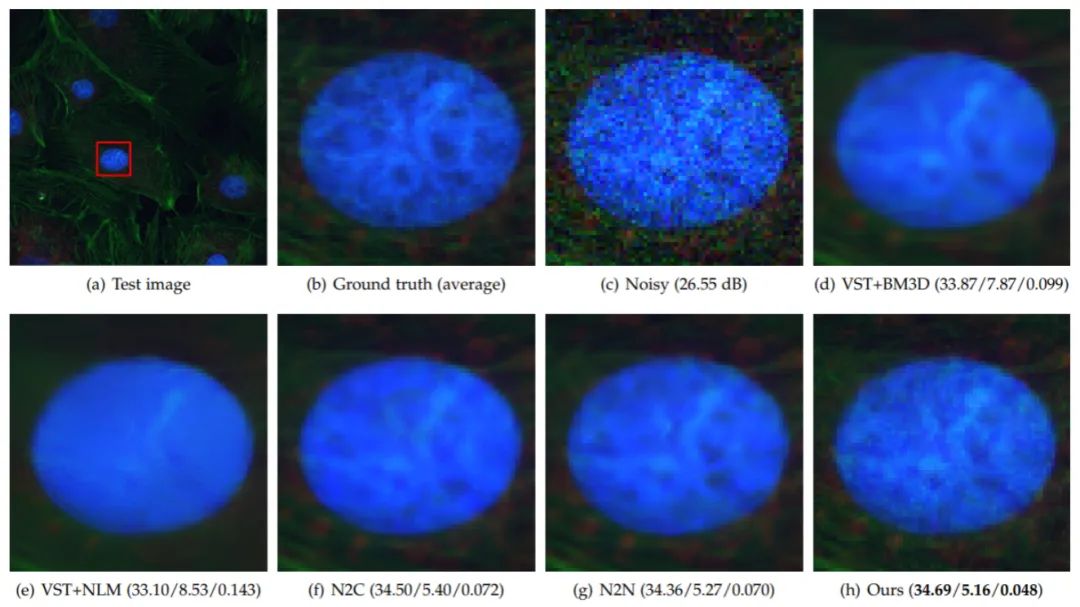
显微镜图像是生物学和医学研究的重要数据来源，然而，由于采集过程中的照明和设备等因素，显微镜图像不可避免地会受到噪声的破坏，从而影响后续的高精度分析。此外，由于没有干净的参考图像，因此需要无监督或自监督的方法。该测试中使用了真实荧光镜图像数据集FMD进行训练和测试。其中使用平均的方法获取近似的Ground Truth。表3展示了真实显微镜图像上的定量比较，所提出方法获得了最高的PSNR、最佳PI和LPIPS分数，如图6所示，所提出方法可以获得比其他方法更清晰的重建结果，这表明了其更好的感知质量。

表3 真实显微镜图像定量比较

图6 真实显微镜图像去噪的视觉比较，括号中为图像的PSNR/PI/LPIPS分数

3.真实深度图像

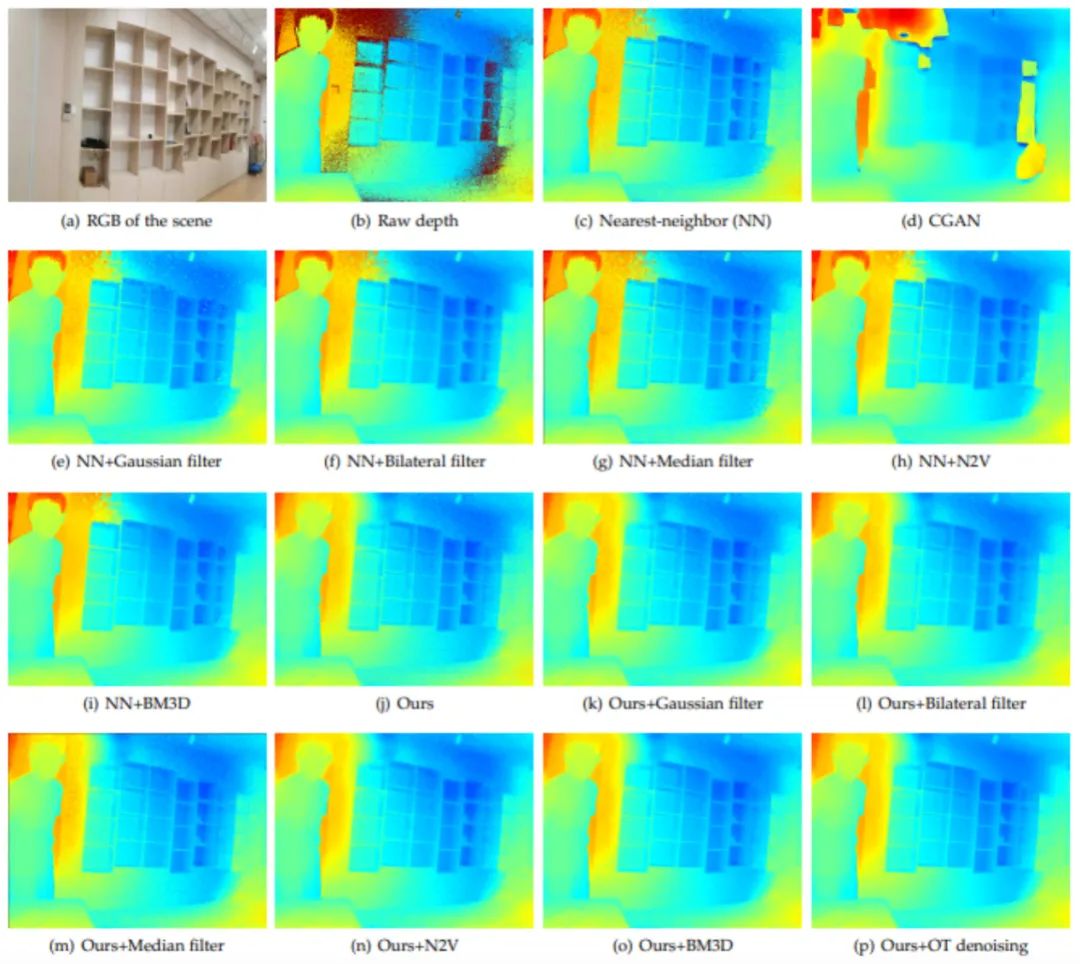
最近，深度相机变得越来越流行，而由于成像机理的不同，深度图像的噪声比RGB图像大得多。此外，由于场景中对象的反射率和透明度较低，深度图像中通常存在空洞（无效像素）。该实验中使用了一台ToF深度相机采集了1430张原始深度图像作为训练和测试集，并使用仿真的SUNCG数据集作为参考的干净图像。图7展示了重建结果的视觉比较，所提出方法可以取得最佳的去噪结果。

图7 原始深度图修复效果比较

图8 原始深度图修复效果，清晰视频demo请见 https://ieeexplore.ieee.org/ielx7/34/4359286/9763342/supp1-3170155.mp4?arnumber=9763342

结论

本项工作在不对退化模型做任何先验假设的条件下，提出了一种基于最优传输理论的无监督图像重建学习准则。该准则可在实现高感知质量重建的同时，最大程度保留原始图像信息。此外，我们在理论上证明了，实际应用中使用的该准则的松弛形式与原始准则具有相同的最优解。大量仿真和真实数据上的实验结果表明，该方法甚至可以与有监督方法相媲美。该方法在具有复杂噪声的深度图像重建上具有非常显著的优越性。此外，虽然本文主要测试了所提框架在降噪任务上的表现，但该框架理论上适用于更广泛的图像重建任务，如超分辨、去雨、去雾等。