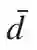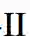【剑桥大学博士论文】模型不确定性下的统计假设检验，198页pdf

统计检验是统计学的主要问题之一，在工程、信号处理、医学、金融等领域有着广泛的应用。传统的假设检验问题中，需要检验的假设分布是已知的。然而，在实践中，真实的分布很难获得。本文研究了具有未知分布的假设检验问题。在本文的第一部分中，我们考虑了独立分布和马尔可夫来源之间的不匹配二元假设检验问题。我们分析了当产生观测值的实际分布不同于在复合设置中的似然比检验、顺序概率比检验和Hoeffding的广义似然比检验中使用的分布时，成对误差概率指数之间的权衡。当真实分布在检验分布的一个小散度球内时，我们定义了每个检验相对于匹配误差指数的最坏情况误差指数。此外，我们考虑了对手篡改观测数据的情况，同样是在观测类型的发散球内。实验表明，这些测试对分布失配比对抗性观察篡改更敏感。在本文的下一部分中，我们提出了一个内曼-皮尔逊设置中的复合假设检验，其中零分布是已知的，替代分布属于某个分布族。该检验在Hoeffding检验和似然比检验之间进行插值，实现了家族中每个分布的最优误差指数权衡。此外，所提出的测试表明可以获得

的第I类错误概率预因子，其中

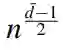
是投影到以零分布为中心的相对熵球上的分布族的维数。这可以显著小于由Hoeffding’s检验实现的预因子

，其中d是概率单纯形的维度。此外，所提出的测试实现了家族中每个分布的最优

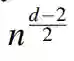
型错误概率预因子。 最后，考虑了二分类内曼-皮尔逊分类的通用分类，其中零分布是已知的，而备用分布只有一个训练序列。该分类器在Hoeffding’s分类器和似然比测试之间进行插值，并获得与似然比测试相同的错误概率预因子，即当两个分布都已知时，具有相同的预因子。此外，与Hoeffding的通用分类器一样，当训练样本与观测样本之比超过某一值时，该分类器可以通过似然比检验获得最优的误差指数折衷。本文提出了训练与观测比的上界和下界。此外，我们提出了一个序列分类器，以达到最优的错误指数折衷。我们还考虑了在尼曼-皮尔逊(Neyman-Pearson)环境下两个分布都未知时的极小极大设置下的分类问题。本文提出的分类器，可以渐进地在ii型和i型错误指数之间实现预定的比例。

https://www.repository.cam.ac.uk/handle/1810/345452