【CMU博士论文】黑盒和多目标优化策略，151页pdf

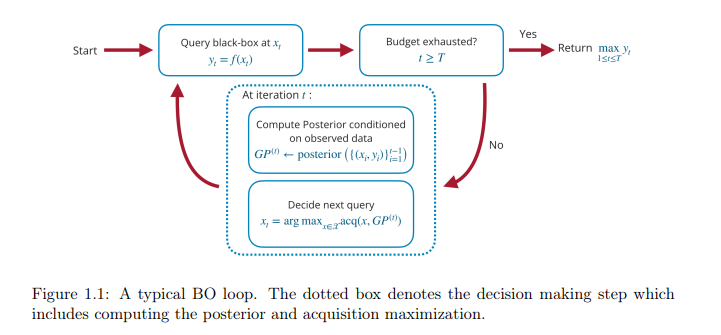
黑盒优化(BBO)问题经常发生在许多工程和科学学科中，在这些学科中，人们可以访问一个函数(黑盒)的零阶评估，该函数必须在特定的领域进行优化。在许多情况下，函数的计算成本很高，因此计算的次数受到预算的限制。贝叶斯优化(Bayesian Optimization)是一种流行的算法，它通过代理对黑箱函数进行建模，并通过评估最有可能导致最优结果的点进行运算。多目标优化(MOO)是优化中的另一个主题，其目标是在一个公共领域中同时优化定义的多个目标。通常情况下，对于相同的输入，这些目标不会达到它们的最佳状态。在这种情况下，不是寻找单一的最佳解决方案，而是需要一组帕累托最优解决方案。本文研究了BBO和MOO的几种优化策略及其应用。

**本文的前半部分是关于昂贵函数的BBO。**首先，基于随机扩展的思想，提出了一种简单而灵活的多目标黑盒优化方法。我们引入了多目标后悔的概念，并表明随着预算的增长，我们的策略实现了零后悔。接下来，我们研究了神经网络对昂贵BBO的有效性。我们证明了一个简单的贪心方法可以达到接近高斯过程贝叶斯优化的性能。利用最近研究的高斯过程和非常广泛的神经网络训练动态之间的联系，我们证明了我们提出的算法的遗憾的上界。最后，我们提出了一个考虑成本的贝叶斯优化框架，该框架考虑了每次评估的成本。这种方法在评估成本随输入域而变化的环境中很有用，低成本评估可以提供关于最大值的大量信息。

本文的后半部分是关于MOO在两个可微MOO问题上的应用。我们的第一个应用是学习稀疏嵌入，使用神经网络进行快速检索。这里要优化的目标是检索精度和检索速度。我们引入了一种新的稀疏正则化方法，并演示了一种退火策略，与其他方法相比，该策略产生了更好的目标帕累托边界。对于我们的第二个应用，我们考虑了分层时间序列预测的问题，其中多个相关的时间序列被组织成一个层次。我们提出了一种考虑层次结构的方法，同时可扩展到大型层次，并表明它在大多数层次级别上都能提高精度。我们还将其视为一个多目标问题，并演示了跨不同层次的性能权衡。为了总结我们的贡献，在这篇论文中，我们提出了各种类型的黑盒和多目标函数的优化策略，并在合成或基准数据集上进行实验评估。