什么是信息几何？索尼Frank NIELSEN研究员最新《信息几何导论》讲解，附45页ppt与视频

什么是信息几何？索尼Frank NIELSEN研究员最新《信息几何导论》讲解，非常值得关注！

信息几何[Ama16, AJLS17, Ama21]旨在解开概率分布族的几何结构，并研究它们在信息科学中的应用。信息学是将统计学、信息论、信号处理、机器学习和人工智能等重新组合起来的一个总称。信息几何是计量经济学家H. Hotelling(1930)和统计学家C. R. Rao(1945)出于数学上的好奇心而独立诞生的，他们考虑了概率分布的参数族，称为统计模型，是一种带有费雪度量张量的黎曼流形[Nie20]。信息几何通过使用微分几何的概念(如曲率)和张量微积分来解决问题。在他的开创性工作中，Rao考虑了流形上的黎曼测地距离和测地球来研究统计学中的分类和假设检验问题。

本文对信息几何(IG)的基本结构进行了简明而现代的介绍，并报告了这些信息几何流形(这里称为“信息流形”)在统计(贝叶斯假设检验)和机器学习(统计混合聚类)中的一些应用。通过类比信息论(IT)(由Claude Shannon在其1948年的著名论文[1]中提出)，它主要考虑在有噪声的传输信道上的信息通信，我们可以将信息科学(IS)定义为研究(有噪声/不完美的)数据和模型家族(假设为先验知识)之间的“通信”的领域。简而言之，信息科学寻求从数据中提取信息到模型的方法。因此，信息科学不仅包括信息理论，还包括概率与统计、机器学习(ML)、人工智能(AI)、数学编程等领域。

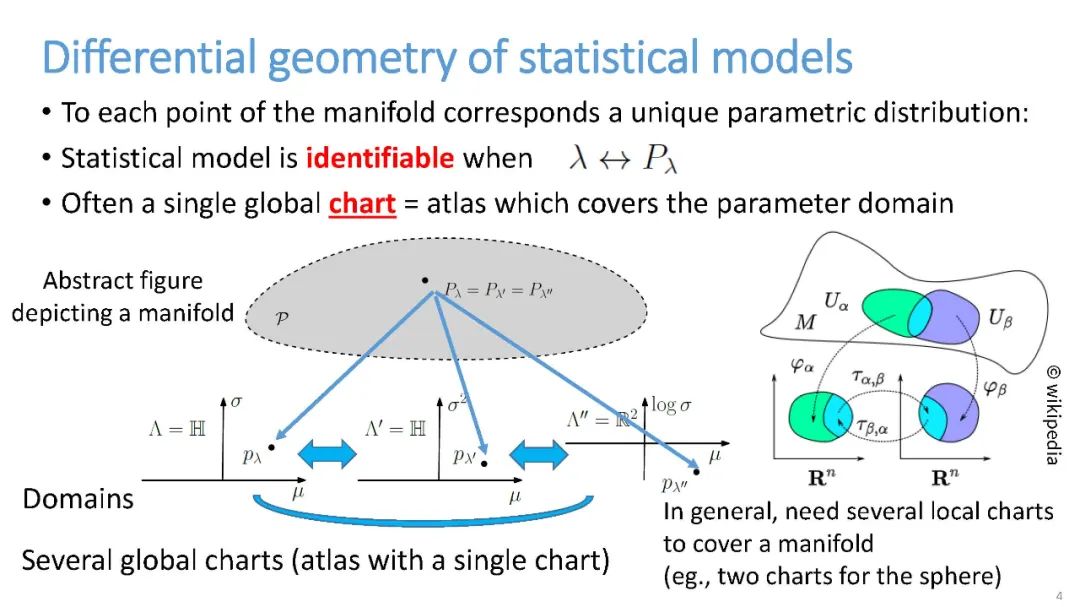
我们回顾了信息几何的一些关键里程碑，并在第5.2节报告了该领域的先驱们的一些定义。现代信息几何的创始人Shun-ichi Amari教授在最新出版的《[2]》教科书的序言中对信息几何下了这样的定义:“信息几何是利用现代几何探索信息世界的方法。”简而言之，信息几何从几何角度研究信息科学。它是一个数学的努力来定义和限制术语本身的几何是开放式的。通常，我们先研究问题的不变性(例如，概率分布之间距离的不变性)，然后得到一个新的几何结构(例如，一个“统计流形”)。然而，一个几何结构是“纯粹的”，因此可以应用到原始问题范围之外的其他应用领域(例如，在数学规划[3]中使用统计流形的二元论结构):几何[4]的方法因此产生了一个外展模式[5,6]。

信息几何的狭义定义可以表述为研究决策几何的领域。这个定义还包括模型拟合(推断)，它可以被解释为如图1所示的决策问题;即，决定从参数模型家族中选择哪个模型参数。这个框架是由Abraham Wald[7-9]倡导的，他认为所有的统计问题都是统计决策问题。差异(也被松散地称为其他之间的距离)不仅在测量数据对模型的拟合度(例如，统计中的可能性、ML中的分类器损失函数、数学规划或运算学中的目标函数等)方面发挥着关键作用，而且在测量模型之间的差异(或偏差)方面也发挥着关键作用。

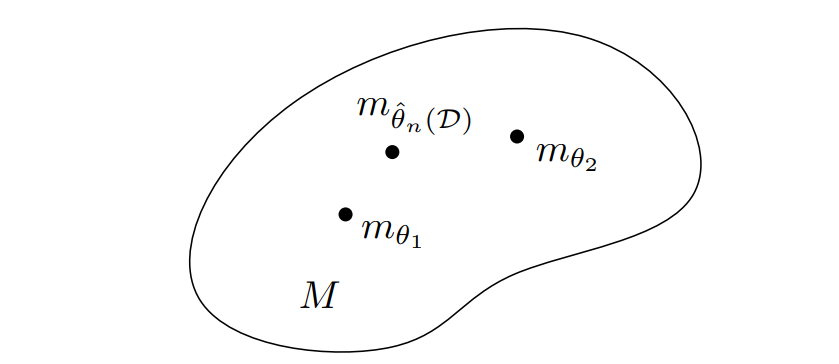
图1.从数据D得出的模型的参数推断ˆθ也可以解释为一个决策问题:决定一个参数模型族M = {M θ}θ∈Θ中的哪个参数最适合该数据。信息几何在流形M上提供了一种微分几何结构，对统计决策规则的设计和研究非常有用。

人们可能会想**，为什么要采用几何方法?**几何学允许人们在一个无坐标的框架中研究“图形”的不变性。几何语言(例如，线、球或投影)也提供支持，帮助我们直观地推理问题。注意，尽管图可以被可视化(例如，绘制在坐标图中)，但它们应该被认为是纯粹的抽象对象，即几何图形。

这篇关于信息几何[2]的综述的目的是在不假设任何微分几何[10]背景的情况下描述流形上的核心二元论结构，并解释几个重要的相关原理和概念，如不变性、协方差、投影、平坦度和曲率、信息单调性等。在此过程中，我们将用选定的例子和应用来说明基本的潜在概念，并将澄清一些潜在的混淆来源(例如，几何统计结构可用于非统计应用[3]，理清α在α连接、α-分歧和α-表示中的含义，等等)。特别地，我们将在第3.5节中命名和说明信息几何的基本定理。我们建议读者参阅书籍[2,4,11 - 17]，以深入探讨该领域及其在信息科学中的应用

Frank Nielsen在INRIA/ Cote d 'Azur(法国)大学获得自适应计算几何博士学位(1996年)。他是索尼计算机科学实验室(Sony CSL, Tokyo)的研究员，目前从事几何机器学习和智能的基础和实践研究。他曾在法国综合理工学院(Ecole Polytechnique, Charles River Media教科书，2005)和数据科学的高性能计算(施普林格UTICS教科书，2016)任教，目前服务于以下期刊:施普林格Information Geometry, MDPI Entropy，和IEEE Transactions on Information Theory。Frank Nielsen与Frederic Barbaresco共同组织了两年一次的信息几何科学会议(GSI LNCS会议)。 https://franknielsen.github.io/