《用于计算稳健和自适应网络流的迭代安全博弈》MIT等2022最新21页论文

我们研究了不确定环境中的稳健和适应性的最大网络流量问题，其中网络参数（如容量）是已知和确定的，但网络结构（如边）容易受到对手的攻击或失败。我们提出了一个稳健和可持续的网络流模型，以有效和主动地对抗在预算约束下运作的对手的合理攻击行为。具体来说，我们引入了一种新的场景生成方法，该方法基于防御者和对手之间的迭代式双人博弈。我们假设对手总是采取最佳的近视反应（在一些可行的攻击中）来对付防御者准备的当前流量场景。另一方面，我们假设防御者考虑到对手在之前的博弈迭代中所揭示的所有攻击行为，以产生一个新的保守的流量策略，该策略对所有这些攻击是稳健的（最大化）。这种迭代博弈一直持续到对手和管理员的目标都趋于一致。我们表明，防御者要解决的稳健网络流量问题是NP-hard，而对手的决策问题的复杂性随着网络规模和对手的预算值呈指数级增长。我们提出了两种原则性的启发式方法来解决大型城市网络规模下的对抗者问题。在多个合成和真实世界数据集上的广泛计算结果表明，与四种最先进的基准方法相比，防御者问题提供的解决方案大大增加了通过网络推送的流量，并减少了预期的流量损失量。

本文的主要贡献有以下几点。

1.我们正式定义了计算关键基础设施网络的稳健和自适应的最大流量策略的问题，即利用一个被破坏的边缘的流量可能通过有剩余容量的相邻的边缘改道的事实。为了解决这个问题，我们提出了一个网络管理员和对手之间的迭代式双人博弈，这被称为网络流量博弈（NFG）。

2.我们开发了新的优化模型来解决双方在博弈的每个迭代中的决策问题。管理者的优化模型考虑到对手在以前的迭代中产生的所有攻击策略，并计算出一个稳健的流量策略，在所有以前的攻击中，在最坏的情况下使通过网络推动的流量最大化。对手的决策问题检查管理员在当前迭代中产生的流量策略，并产生一个攻击（在给定预算约束下的可行攻击中），以最佳方式破坏当前流量策略。

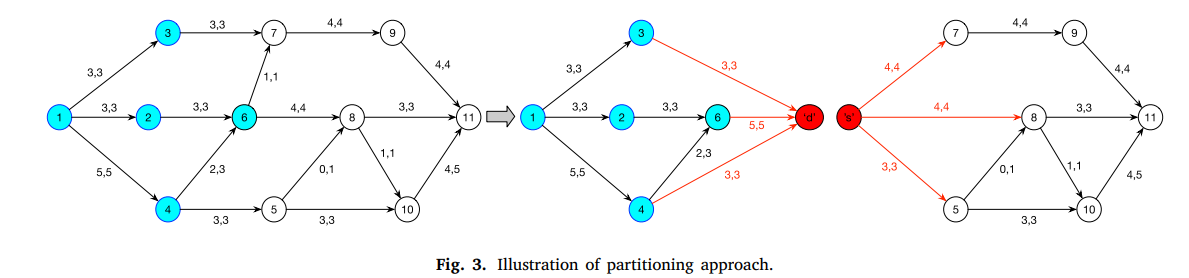
3.我们提出了两种新的启发式方法，用于解决大型城市网络规模下的对手的复杂决策问题。第一种启发式方法是一种加速的贪婪方法，它可以逐步确定要攻击的最佳边缘。第二种启发式方法是一种基于网络分区的方法，它迭代地确定网络中要攻击的一组最佳候选边，然后在这些候选边上解决对手的决策问题。

4.我们在多个合成和真实世界的基准数据集上提供了大量的计算结果，以证明我们提出的解决方法可以优雅地扩展到大规模的问题，并且比四个最先进的基准方法显著增加了通过网络推送的流量。