【多机器人任务分配】《通过学习的子团队性能对异构多机器人路由问题进行分层规划》美国陆军、MIT等2022最新论文

本文考虑了一类特殊的多机器人任务分配问题，其中任务对应于定义在特定环境的不同区域的异质多机器人路由问题。我们提出了一个分层规划器，将这个问题的复杂性分解为两个子问题：将机器人分配到路由任务的高层问题，以及计算每个子团队的实际路由路径的低层问题。规划者使用图形神经网络（GNN）作为启发式方法来估计特定联盟在特定路由任务上的子团队表现。然后，随着底层问题解决方案的出现，它将估计值迭代细化为实际的子团队性能。在一个以异构多机器人区域检查问题为基础路由任务的测试平台问题上，我们的经验表明，我们的分层规划器能够计算出最优或接近最优（7%以内）的解决方案，比事先计算所有可能的分配计划以获得精确的路由时间的最优基线快16倍左右（平均而言）。此外，我们表明，与其他基线（非学习型）估计器相比，基于GNN的估计器可以在解决方案的质量和计算时间之间提供出色的权衡。

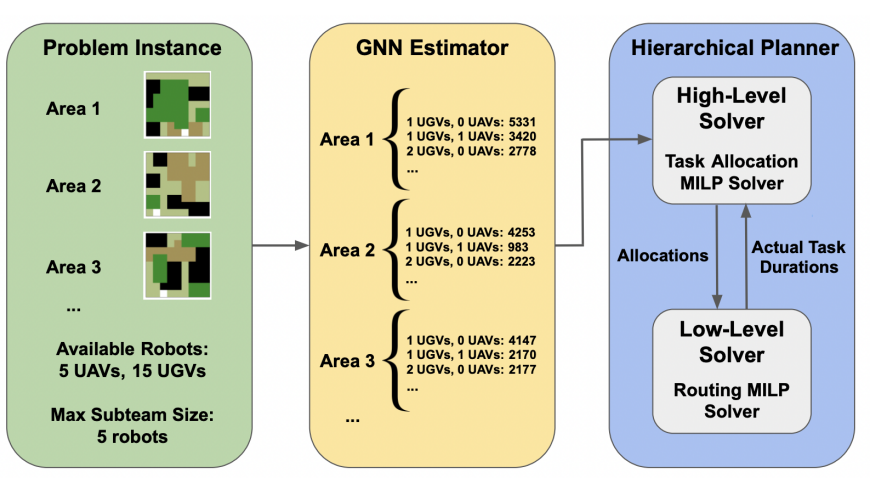
图 1：应用于我们的测试平台问题的拟议分层规划框架。 GNN 首先用于估计不同子团队检查环境不同区域所需的时间。高级求解器使用这些估计来计算高级分配，而低级求解器使用专门的路由算法计算实际路径。然后使用实际任务持续时间来更新高级求解器的 GNN 估计，然后可以使用改进的估计集计算新的分配。

I 引言

本文考虑了一类特殊的多机器人任务分配问题，其中任务对应于定义在特定环境的不同区域的异质多机器人路由问题。目标是最小化完成所有路由任务所需的时间。这类问题代表了一些场景，在这些场景中，将机器人的子团队分配到各个区域将是有益的。例如，在跨越非常大的环境的搜索和救援行动中，电池的限制可能使一个机器人不能被用于一个以上的区域。另外，在军事场景中，战略区域可能需要在车队通过之前同时检查是否有对手存在。作为最后一个例子，考虑一个通信受限的巡逻场景，将子团队分配到各个区域可以保证机器人将有足够的组间网络，以迅速响应对入侵者的检测。这些类型的问题本质上显示了一个层次结构：如果我们事先知道每个可能的机器人子团队完成每个可能的路由任务所需的时间，我们可以首先确定子团队对感兴趣区域的最佳分配，然后只计算该分配的实际子团队路径。优化处理第一阶段的一个直接方法是预先计算所有可能的子团队任务分配的路径，这将提供所有可能的路由时间作为一个副产品。不幸的是，即使不考虑分配问题的组合性，通常情况下，由子团队分配产生的多机器人路由问题是NP-hard，只有通过计算昂贵的算法方法才能得到一个好的解决方案，例如将路由问题表述为混合整数线性程序（MILP），通常需要几秒钟到几分钟或几小时的运行。为了减少整体规划时间，寻找一个好的分配应该以懒惰的方式解决路由任务问题，从最有希望的子团队分配给任务开始。然而，知道一个分配的潜在效用通常需要知道它的路由计划，消除了懒惰方法的优势。

我们注意到，子团队的分配只需要知道给定分配的不同路由计划的成本，而不是实际计划本身。如果我们能够估计这些成本，而不同时解决相应的路由问题，我们就可以推迟计算路由计划，直到决定了一个暂定的分配。

基于这些观察，我们提出了一个分层规划器，能够将原始问题的复杂性分解为两个自然的子问题：将机器人分配到路由任务的高层次问题，以及只为所有可能分配给子团队的区域中的一个选定子集计算实际路由路径的低层次问题。由于多机器人路由问题通常是在图形表示的环境中定义的，规划者使用图形神经网络（GNN）作为启发式方法来估计特定联盟在特定路由任务中的子团队性能。迭代后，计划者将这些估计值细化为真正的子团队性能，因为低层问题的解决方案已经可用。我们引入了一个测试平台问题，其中有一个异构多机器人区域检查问题作为基本的路由任务，对此我们再次考虑了基于传统混合整数线性编程表述的解决方法。图1显示了拟议的规划框架的示意图。

在包含多达45个机器人和20个检查区域的路由任务分配问题中，我们的经验表明，我们的方法总是能够计算出最优或接近最优（7%以内）的解决方案，比事先计算所有可能分配的计划以获得精确的路由时间的最优基线快16倍（平均）。我们还表明，与其他基线（非学习型）估计器相比，基于GNN的估计器在解决方案的质量和计算时间之间提供了一个很好的权衡。