【GNN】图神经网络入门之GRN图循环网络

本文是清华大学刘知远老师团队出版的图神经网络书籍《Introduction to Graph Neural Networks》的部分内容翻译和阅读笔记。
个人翻译难免有缺陷敬请指出，如需转载请联系翻译作者 

作者：Riroaki

原文链接：https://zhuanlan.zhihu.com/p/135366196

除了GCN，还有一种趋势是在传播步骤中使用诸如GRU或LSTM等RNN的门控机制，以减少来自基本GNN模型的限制并提高整个图上的长期信息传播。

GATED GRAPH NEURAL NETWORKS（GGNN）

GGNN网络使用了GRU（Gate Recurrent Units），在固定的 T 时间步中展开RNN，并使用BPTT算法（Back Propagation Through Time）以计算梯度。

补充：
GGNN并不能保证图的最终状态会到达不动点。由于更新次数 T 变成了固定值，因此GGNN可以直接使用BPTT算法来进行梯度的计算。相比于一般的GNN使用Almeida-Pineda算法需要更多的内存，但是不需要约束参数以满足压缩映射（contraction map）的要求。
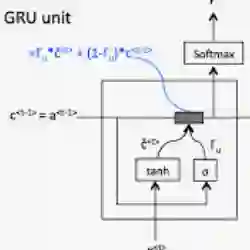
补充一下GRU的基本传播步骤：

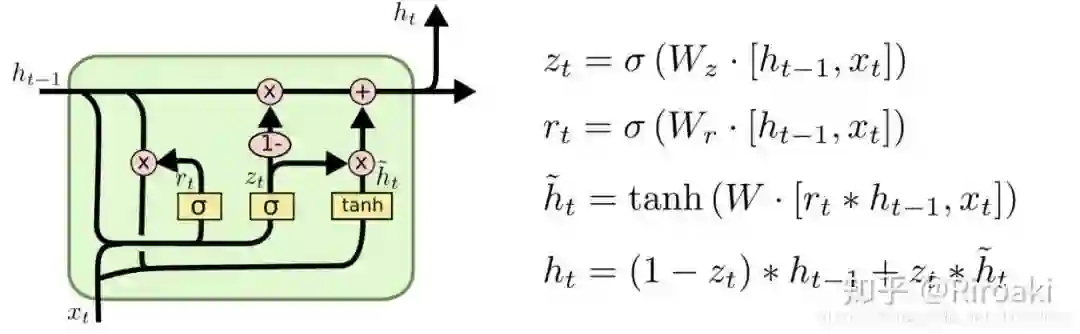
使用了GRU的GGNN模型的基本传播步骤为：

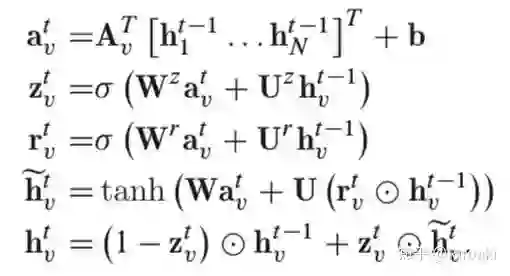
节点 v 首先聚合来自其相邻节点的信息，其中  是图邻接矩阵 A 的子矩阵，并表示节点 v 与相邻节点的连接。类似于GRU的更新函数使用来自每个节点邻居的信息以及上一个时间步的信息来更新节点的隐藏状态。向量 a 聚合节点 v 的邻域信息，z 和 r 是更新和重置门，  是Hardamard按位乘积运算。

GGNN模型是为解决图上定义的问题而设计的——这些图需要输出序列，而现有模型则专注于产生单个输出。

补充：
对于不同任务，GGNN模型具有不同的输出：
对于节点层级（node-focused）的任务，模型对每个节点都有一个输出向量；
对于图级别（graph-focused）的任务，模型可以在节点向量基础上获得图的表示向量。

在GGNN基础上进一步提出的GGS-NNs（Gated Graph Sequence Neural Networks），使用多个GGNN网络来生成输出序列  。

补充：
节点标注（node annotations）记为   并不是最终的节点表示   ，这与一般的GNN不同。在一般的GNN中，由于迭代过程最终会收敛到不动点，故初始化节点表示表示没有意义。但是在GGNN中，由于迭代过程并不一定收敛，初始化的节点表示会影响最终结果，故需要将节点标注作为额外的信息输入模型。
 甚至可以是不同维度的——使用前者初始化后者的时候需要进行padding补齐。

如下图由两个GGNN组成的GGS-NNs网络，其中  为在第 k 步输出中的节点标注，GGNN网络  利用  预测  ，  利用  预测  。

我们使用  来表示在第 k 个输出步中第 t 传播步骤的节点向量，其中  用  的值更新。这里的  可以是共享权值的网络，也可以是单独的网络，看目标是否需要两个网络有不同的作用。

补充：
这里原文貌似笔误，提到   ，如果按照符号来说应该是   ，此处存疑……希望有不同理解的朋友能分享一下。

---

TREE LSTM

在基于树或图的传播过程中，LSTM也以与GRU相似的方式使用。有工作提出了对基本LSTM体系结构的两个扩展：Child-Sum Tree-LSTM和N-ary Tree-LSTM。

• Child-Sum Tree-LSTM （Dependency Tree-LSTM）

像在标准LSTM单元中一样，每个Tree-LSTM单元（由v索引）都包含输入和输出门，存储单元和隐藏状态。标准LSTM单元使用单个遗忘门，Tree-LSTM单元则具有多个遗忘门，对每个子节点 k 使用一个遗忘门  ，从而允许节点 v 相应地聚合来自其子节点的信息。

补充：
另外一个不同是，Tree-LSTM使用子节点上一步的隐藏输出之和，即   用于取代标准LSTM的   。

Child-Sum Tree-LSTM的公式为：

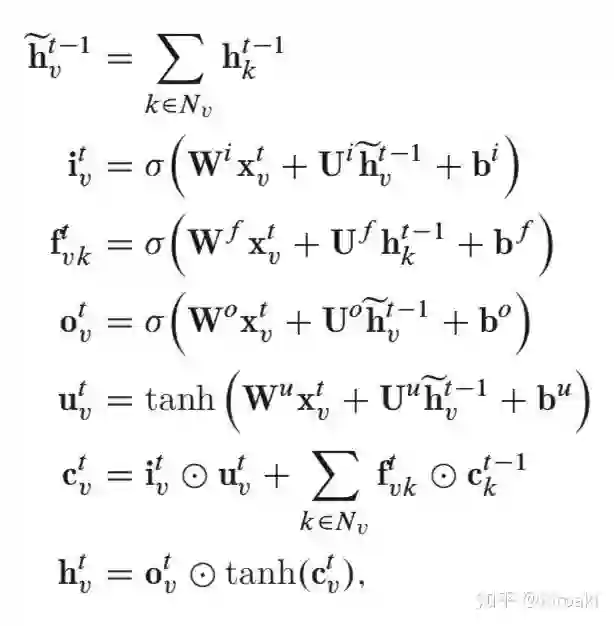
其中  是标准LSTM设置中时间步 t 的输入向量。

补充：
Child-Sum Tree-LSTMs将其子节点的状态   进行累加，因此适合 多分支、子节点无序的树，例如dependency tree, 一个head的dependent数量是高度可变的，因此将应用在dependency tree上的Child-Sum Tree-LSTM称为  Dependency Tree-LSTM.

• N-ary Tree-LSTM (Constituency Tree-LSTM)

如果树中每个节点的子节点数最多为 K ，并且这些子代可以从 1 到 K 进行排序，则可以应用 N-array Tree-LSTM。对于节点 v ，  和  分别表示其在时间 t 的第 k 个子节点的隐藏状态和存储单元。过渡方程如下：

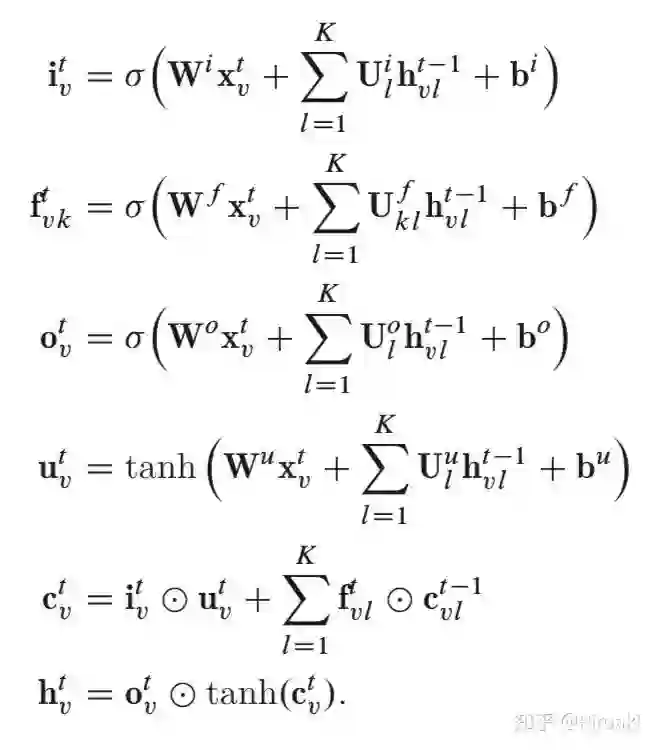
与Child-Sum Tree-LSTM相比，N-ary Tree-LSTM为每个子节点引入了单独的参数矩阵，这使模型可以了解以其子为条件的每个节点的更精细的表示。

补充：
Constituency Tree-LSTM是N-ary Tree-LSTM在N=2的特例，更为常见（或者说是因为在原论文《Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks》中作为典型例子被使用）。

---

GRAPH LSTM

上文提及的两种类型的Tree-LSTM可以轻松适配图问题。Zayats和Ostendorf [2018]中的图结构LSTM是应用于该图的N-ary Tree-LSTM的示例。但是，它是个简化版本——因为图中的每个节点最多具有两个传入边（来自其父级和同级前辈）。Peng等[2017]基于关系提取任务，提出了Graph LSTM的另一个变体。图和树之间的主要区别在于图中的边也有标签。彭等[2017]利用不同的权重矩阵表示不同的标签：

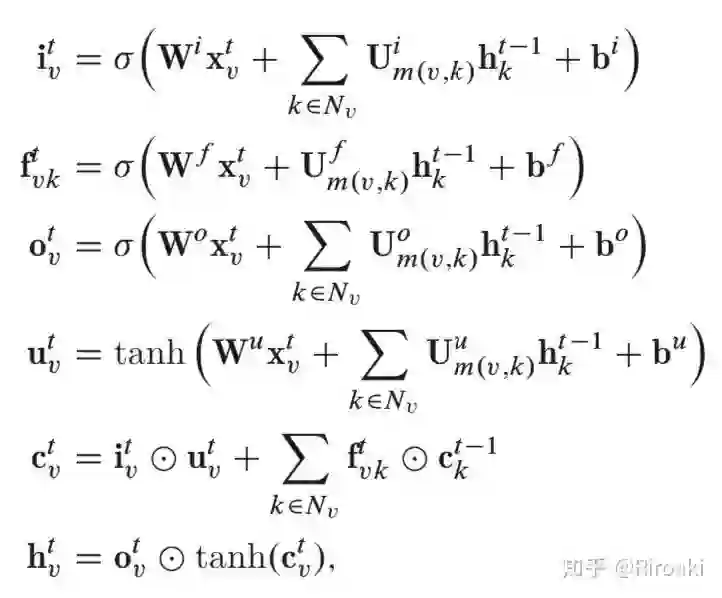
Liang等[2016]提出了一个Graph LSTM网络来解决语义对象解析任务。它使用置信度驱动方案来自适应选择起始节点并确定节点更新顺序。它遵循将现有LSTM通用化为图结构数据的相同想法，但是具有特定的更新顺序，而我们上面提到的方法与节点的顺序无关。

本块内容较简略，感兴趣者可以阅读有关论文（按上文引用顺序排列）：
《Conversation modeling on reddit using a graph-structured LSTM》
《Cross-sentence N-ary relation extraction with graph LSTMs》
《Semantic object parsing with graph LSTM》

---

SENTENCE LSTM

Zhang等[2018c]提出了用于改进文本编码的Sentence-LSTM（S-LSTM）。它将文本转换为图形，并利用Graph-LSTM学习表示形式。S-LSTM在许多NLP问题中显示出强大的表示能力。

具体地，S-LSTM模型将每个单词视为图中的一个节点，并添加了一个超节点（supernode）。对于每一层，单词节点可以聚合来自其相邻单词以及超节点的信息。超节点可以聚合来自所有单词节点及其自身的信息。不同节点的连接可以在下图中找到。

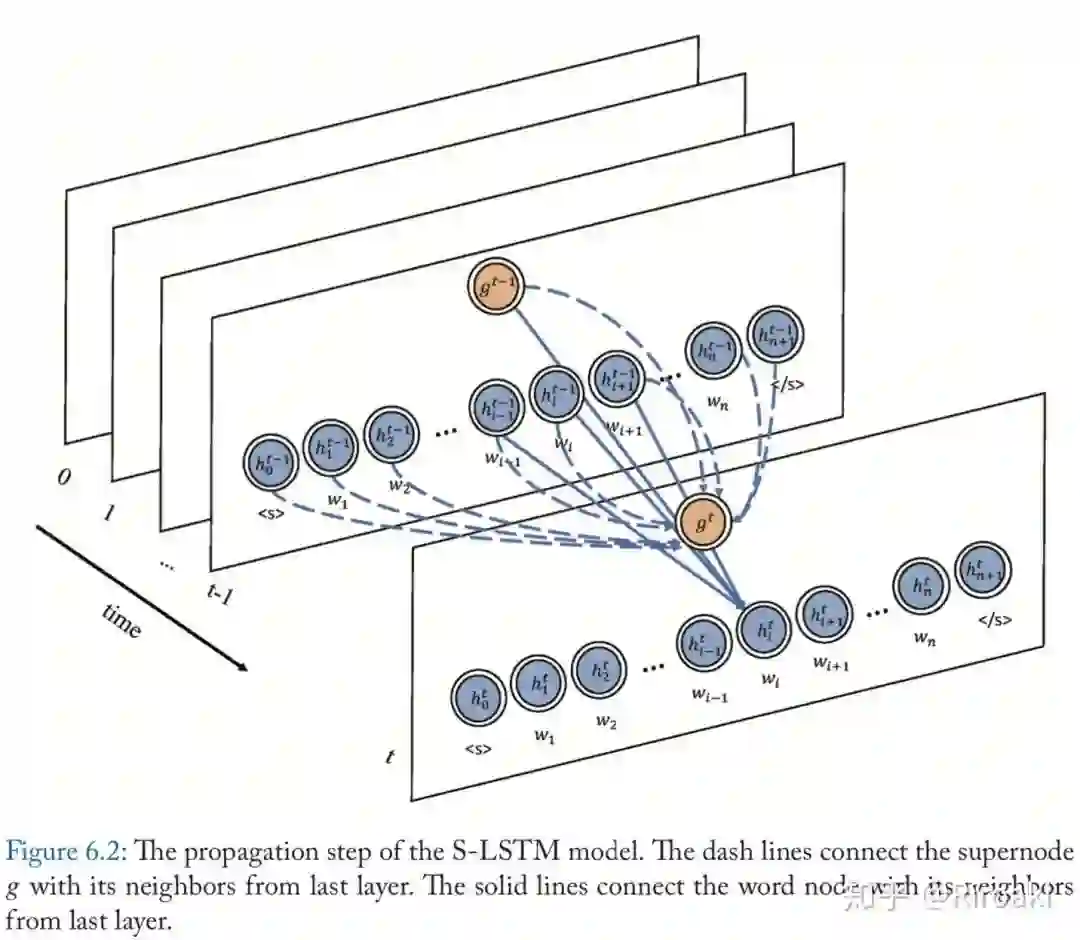
这些连接设置背后的原因是，超节点可以提供全局信息来解决长距离依赖性问题，而单词节点可以从其相邻单词建模上下文信息。因此，每个单词都可以获取足够的信息并对局部和全局信息进行建模。

S-LSTM模型可用于许多自然语言处理（NLP）任务。单词的隐藏状态可用于解决单词级别的任务，例如序列标记，词性（POS）标记等。超节点的隐藏状态可用于解决句子级任务，例如句子分类。该模型在多项任务上均取得了令人鼓舞的结果，并且也胜过了强大的Transformer模型（！！！）。

---

投稿或交流学习，备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多： 机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦