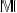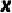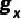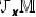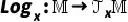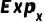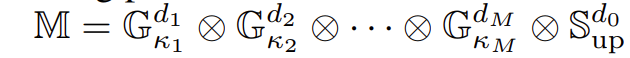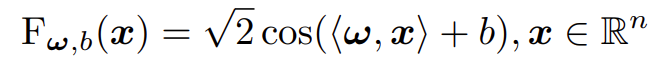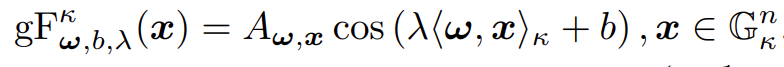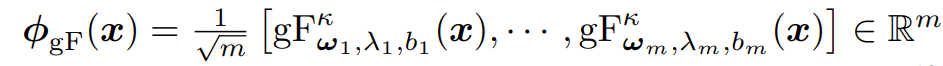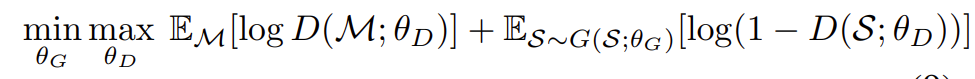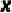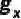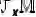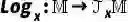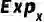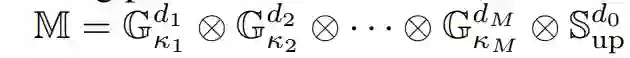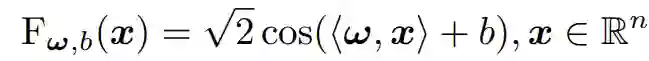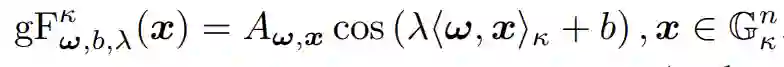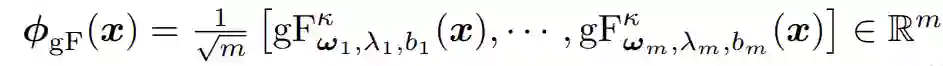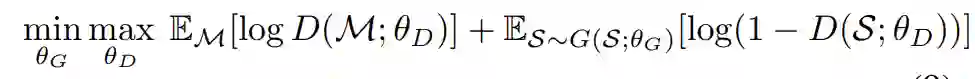![]()
论文标题:Motif-aware Riemannian Graph Neural Network with Generative-Contrastive Learning论文作者:Li Sun, Zhenhao Huang, Zixi Wang, Feiyang Wang, Hao Peng, Philip S. Yu作者单位:华北电力大学, 北京航空航天大学,UIC论文链接:https://arxiv.org/abs/2401.01232
代码链接:https://github.com/RiemannGraph/MotifRGC 01.摘要图是复杂结构的典型非欧几里得数据。近年来,黎曼图表示学习已经成为欧几里得图表示学习中一个十分有效果的替代方案。然而,黎曼方法仍处于早期阶段:大多数呈现单一曲率(半径),而不考虑结构复杂性,同时由于指数/对数映射而易遭受数值不稳定性,并且缺乏捕捉模体规律性的能力。鉴于上述问题,我们提出了模体感知的黎曼图表示学习问题,寻求一种数值稳定的、无监督的编码器来捕捉多曲率流形中的模体模式。为此,我们提出了一种新的带有生成-对比学习的主题感知黎曼模型(MotifRGC),该模型以自监督的方式在黎曼流形上进行极小-极大化博弈。首先,我们提出了一种新的黎曼GCN (D-GCN),用一个具有多样化因子的积层构造一个多样化曲率流形,并用一个稳定的核层代替指数/对数映射。其次,引入了一种基元感知的黎曼生成-对比学习,在构造的流形中捕捉模体模式,并在没有外部标注的情况下学习模体感知的节点表示。
02.背景
图卷积网络(Graph Convolutional Networks, GCNs)已经成为了学习图表示的主流方法,其通过基于邻居结构的信息传递,学习和提取图的特征表示。然而,传统的GCNs通常在欧几里得空间中进行信息传递,这在一定程度上限制了它们处理具有复杂结构的非欧几里得数据的能力。近年来,将图数据嵌入到Riemannian manifold(黎曼流形)中进行学习的方法逐渐崭露头角,这类方法被称为Riemannian GCN。黎曼图神经网络的研究仍然处于早期阶段,还有几个问题亟待解决:1、现有方法使用的是单一曲率(半径),但是存在大量的图由多个曲率不相同的部分组成。2、在欧氏空间-黎曼空间的映射过程中,指数/对数映射是常用操作。但是,这两者并非数值稳定的算子。3、motif是构筑图的基本单元,对图结构的理解有着至关重要的作用。但是在现有的黎曼空间模型研究中极少被提及。本文旨在自监督学习的场景中,通过构建多曲率流形来捕捉图数据的复杂结构,进而提升模型对图数据的理解和学习能力。2.1 黎曼流行Riemannian manifold黎曼流形是一个光滑流形,是对曲面概念的一种广义化,相比较一般的流形,它拥有一个额外的结构——黎曼度量。在黎曼流形
![]() 上,每一点
上,每一点![]() 的黎曼度量
的黎曼度量![]() 都定义在其切空间(Tangent Space)
都定义在其切空间(Tangent Space)
![]() 上。对数映射
上。对数映射![]() 将流形中的向量变换到切空间上,而指数映射
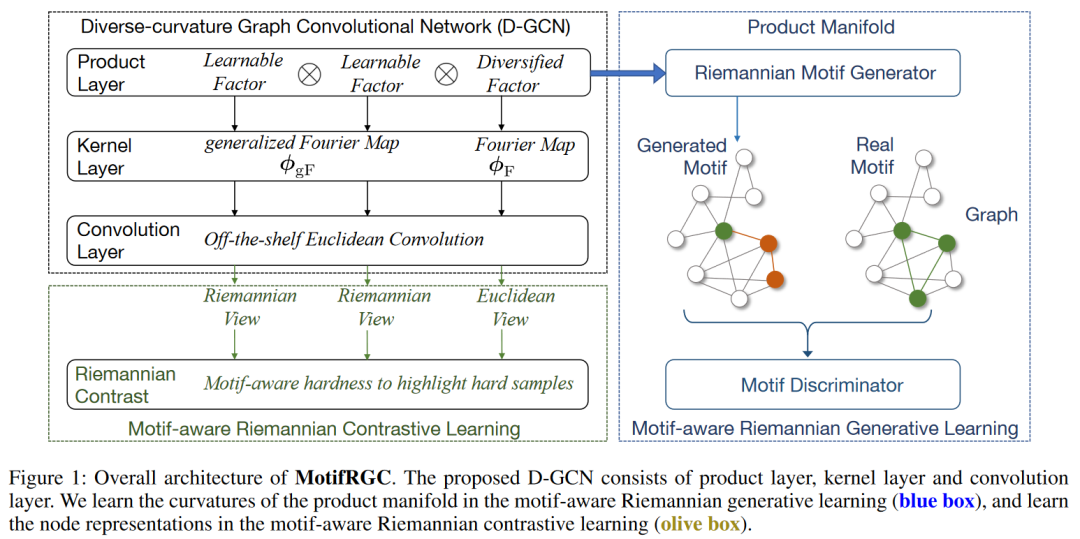
将流形中的向量变换到切空间上,而指数映射![]() 进行逆变换。欧几里德空间是黎曼流形的一种特殊情况。 黎曼流形的另一个重要性质是曲率。曲率描述了流形如何局部地偏离欧几里得空间。当流形中每个点的曲率相等时,称其为单曲率流形。具体来说,当单曲率为负时,流形是双曲H;当单曲率为正时,流形是超球S。而多样曲率流形则是指点的曲率不相同的流形。以往的黎曼流形上的工作大多研究单曲率流形中的图,事实上多样曲率流形可以更好地匹配真实图的复杂结构。我们的工作就是基于对多样曲率流形的研究。2.2 模体Motif在图论中,motif是指一个固定的、有向或无向的子图,它由一组顶点和连接这些顶点的边组成。这个子图可以是简单的三角形、四边形或其他形状,关键在于它在原始图中以相同的方式重复出现。在图神经网络中,motif是一种重要的结构特征,它反映了图的基本模式和规律。在Riemannian manifold中,我们通过引入motif-aware Riemannian generative-contrastive learning,充分利用了motif的这一特性。 03.模型架构模型的整体架构如图1所示。我们首先提出了一个新的图卷积网络——多曲率图卷积网络(Diverse-curvature GCN,D-GCN)。在构建模型时,我们通过引入一个乘积层来实现多样化曲率。这个乘积层将每个节点映射到多个可学习的黎曼特征,并通过这些特征来构造出多曲率流形。特别地,为了确保曲率的多样性,我们在设计中引入了一个多样化因子。这个多样化因子不仅丰富了模型的表达能力,而且也为模型带来了更好的适应性。 针对数值稳定问题,我们基于Bochner定理提出了一种数值稳定的映射方法。这种方法不仅避免了指数/对数映射的问题,而且还能够更好地捕捉图的结构复杂性。通过这种方式,所提出的模型能够在没有标签的情况下,自监督地学习图数据的复杂结构,从而有效地捕获图中的motif规律性。然后,我们在流形中设计了一个Riemannian motif生成器,用于生成假motif。这些假motif被送入判别器,与从图中采样的真实motif进行对比。生成器和判别器之间形成了一个对抗的过程,通过这个min-max game,模型能够学习到捕获motif规律的曲率,使得生成的假motif和真实的motif无法被判别器区分出来。这种基于motif的学习方式,使模型能够更好地捕捉图的结构复杂性,从而提高了模型的性能。
进行逆变换。欧几里德空间是黎曼流形的一种特殊情况。 黎曼流形的另一个重要性质是曲率。曲率描述了流形如何局部地偏离欧几里得空间。当流形中每个点的曲率相等时,称其为单曲率流形。具体来说,当单曲率为负时,流形是双曲H;当单曲率为正时,流形是超球S。而多样曲率流形则是指点的曲率不相同的流形。以往的黎曼流形上的工作大多研究单曲率流形中的图,事实上多样曲率流形可以更好地匹配真实图的复杂结构。我们的工作就是基于对多样曲率流形的研究。2.2 模体Motif在图论中,motif是指一个固定的、有向或无向的子图,它由一组顶点和连接这些顶点的边组成。这个子图可以是简单的三角形、四边形或其他形状,关键在于它在原始图中以相同的方式重复出现。在图神经网络中,motif是一种重要的结构特征,它反映了图的基本模式和规律。在Riemannian manifold中,我们通过引入motif-aware Riemannian generative-contrastive learning,充分利用了motif的这一特性。 03.模型架构模型的整体架构如图1所示。我们首先提出了一个新的图卷积网络——多曲率图卷积网络(Diverse-curvature GCN,D-GCN)。在构建模型时,我们通过引入一个乘积层来实现多样化曲率。这个乘积层将每个节点映射到多个可学习的黎曼特征,并通过这些特征来构造出多曲率流形。特别地,为了确保曲率的多样性,我们在设计中引入了一个多样化因子。这个多样化因子不仅丰富了模型的表达能力,而且也为模型带来了更好的适应性。 针对数值稳定问题,我们基于Bochner定理提出了一种数值稳定的映射方法。这种方法不仅避免了指数/对数映射的问题,而且还能够更好地捕捉图的结构复杂性。通过这种方式,所提出的模型能够在没有标签的情况下,自监督地学习图数据的复杂结构,从而有效地捕获图中的motif规律性。然后,我们在流形中设计了一个Riemannian motif生成器,用于生成假motif。这些假motif被送入判别器,与从图中采样的真实motif进行对比。生成器和判别器之间形成了一个对抗的过程,通过这个min-max game,模型能够学习到捕获motif规律的曲率,使得生成的假motif和真实的motif无法被判别器区分出来。这种基于motif的学习方式,使模型能够更好地捕捉图的结构复杂性,从而提高了模型的性能。
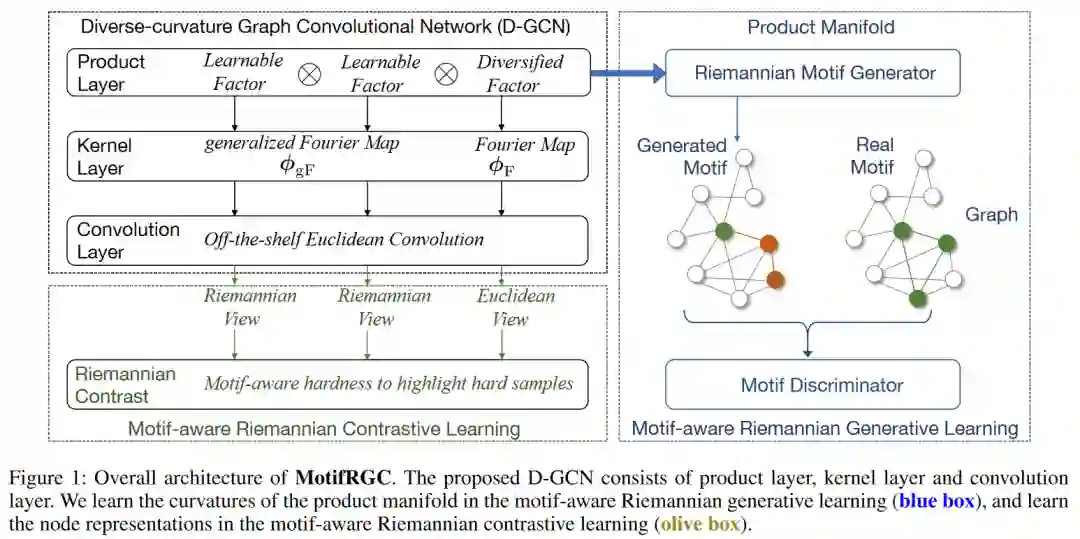
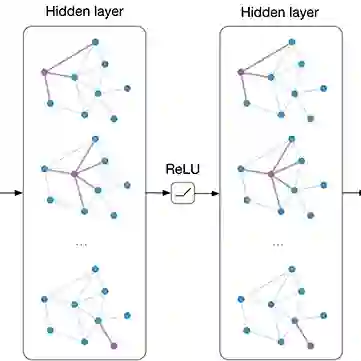
![]() 图1: 模型的整体架构 04.方法概述 4.1 Product layer:多个可学习单曲率因子和一个多样化因子的笛卡尔乘积。
图1: 模型的整体架构 04.方法概述 4.1 Product layer:多个可学习单曲率因子和一个多样化因子的笛卡尔乘积。![]() 4.2 Kernel layer:通过陀螺向量核将黎曼特征转换到欧几里得空间,然后利用成熟的欧式GCN层来更新节点表示。为了解决这种空间变换,我们建立了一个基于广义傅立叶变换的黎曼特征。
4.2 Kernel layer:通过陀螺向量核将黎曼特征转换到欧几里得空间,然后利用成熟的欧式GCN层来更新节点表示。为了解决这种空间变换,我们建立了一个基于广义傅立叶变换的黎曼特征。![]()
![]()
![]() 理论贡献:1.上述黎曼特征可应用于任意曲率,并构建了平移不变核。2.当曲率为-1时,上述核函数为“泊松核”。4.3 Min-max game:黎曼生成-对比学习。生成器G和判别器D进行以下优化。
理论贡献:1.上述黎曼特征可应用于任意曲率,并构建了平移不变核。2.当曲率为-1时,上述核函数为“泊松核”。4.3 Min-max game:黎曼生成-对比学习。生成器G和判别器D进行以下优化。![]() 4.4 Motif-aware Riemannian Contrast:引入了Motif感知强度来学习节点表示的硬样本。首先,生成多个几何视图,每个因子流形提供相应的几何视图。每个几何视图与欧几里得视图对比。因此正样本互相接近,负样本互相远离。此外我们利用Motif来区分正/负样本。直观地说,Motif中的节点彼此相似,被认为是正样本。因此,我们给出motif-aware hardness,以突出硬样本,即低相似度的正样本和高相似度的负样本。 05.实验效果
4.4 Motif-aware Riemannian Contrast:引入了Motif感知强度来学习节点表示的硬样本。首先,生成多个几何视图,每个因子流形提供相应的几何视图。每个几何视图与欧几里得视图对比。因此正样本互相接近,负样本互相远离。此外我们利用Motif来区分正/负样本。直观地说,Motif中的节点彼此相似,被认为是正样本。因此,我们给出motif-aware hardness,以突出硬样本,即低相似度的正样本和高相似度的负样本。 05.实验效果![]()
![]()
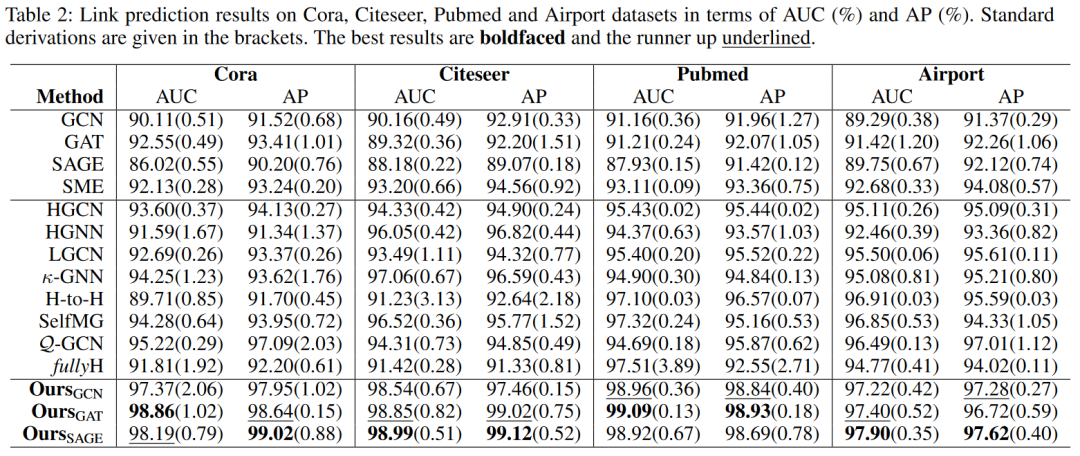
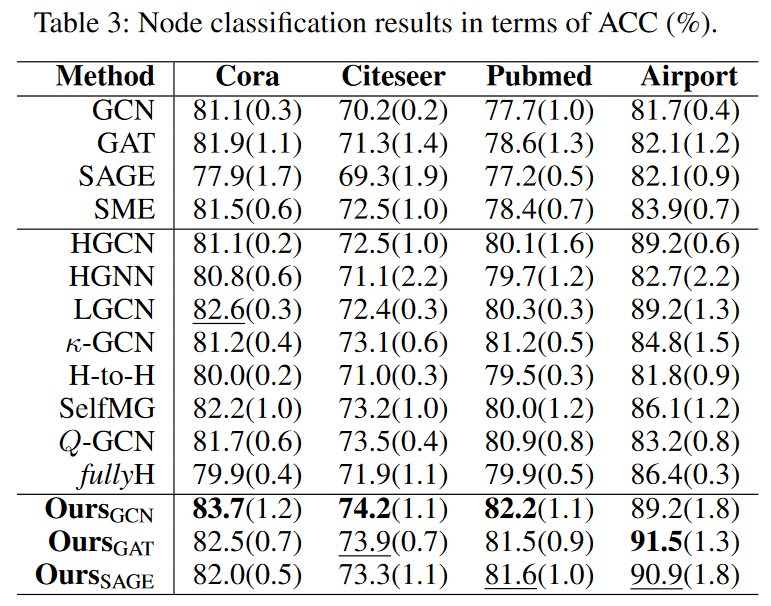
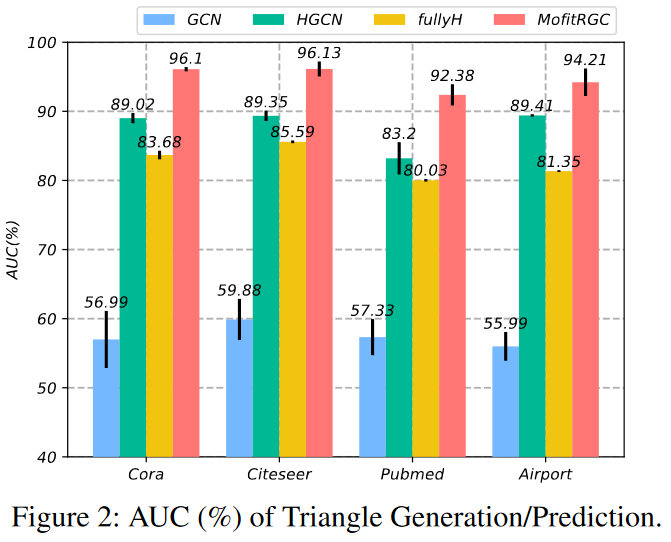
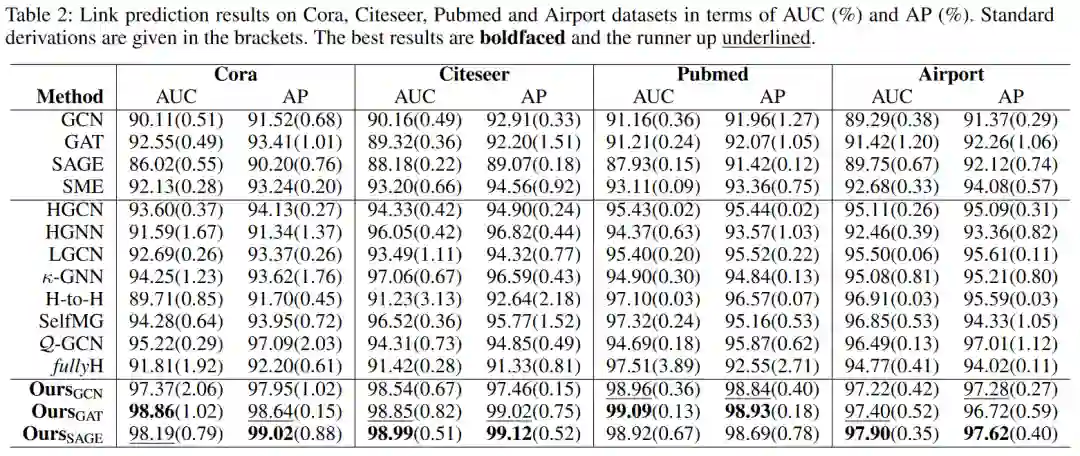
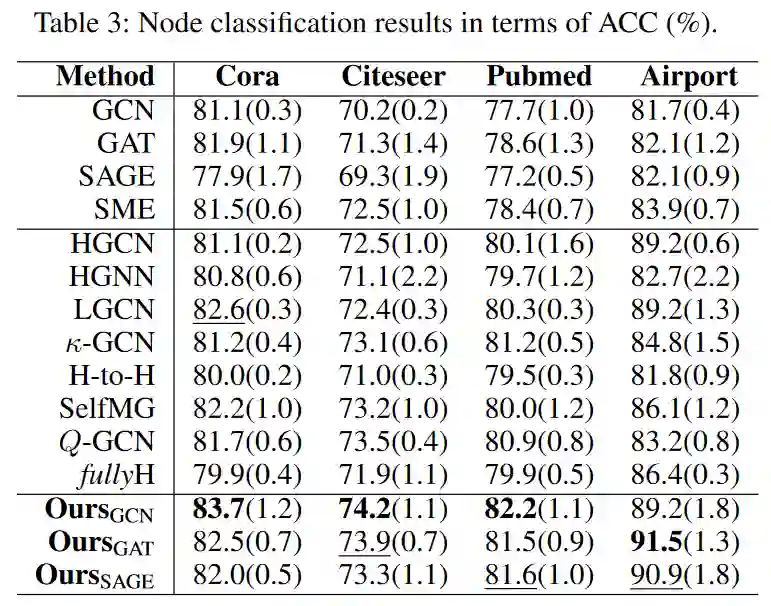
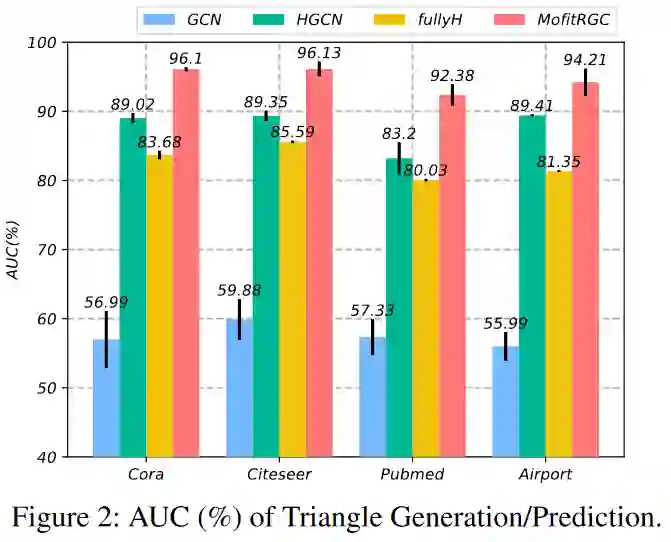
![]() 实验选择了四个常用的标准图数据集:Cora, Citeseer, Pubmed和Airport。我们将提出的MotifRGC模型与欧式空间中常见的GAT,GCN,SAGE等进行对比和黎曼空间中的SOTA GNN模型进行了对比:1.HGCN:Hyperbolic Graph Convolutional Neural Networks, NIPS192.HGNN:Hyperbolic Graph Neural Networks, NIPS193.LGCN:Lorentzian Graph Convolutional Networks, WWW214.k-GCN:Constant Curvature Graph Convolutional Networks, ICML20.5.H-to-H:A Hyperbolic-to-Hyperbolic Graph Convolutional Network, CVPR21. 6.SelfMG:我们AAAI22的工作7.Q-GCN:Pseudo-Riemannian Graph Convolutional Networks, NIPS22.8.fullyH:Fully Hyperbolic Neural Network, ACL22实验结果充分展示了Diverse-curvature GCN在多个数据集上的出色性能。从实验数据可以看出,无论是在链接预测还是在节点分类任务上,Diverse-curvature GCN都取得了显著的提升。消融实验见原文。对于生成的Motif三角形,我们也进行了研究。具体来说,在GCN的基础上实例化MotifRGC,并通过给定三角形的AUC度量来评估生成的三角形。当三角形的三条边都被正确预测的时候,就认为三角形被正确预测。结果表面,Motif的黎曼流形能够更好的捕获图中Motif的结构。 06.结论Diverse-curvature GCN以其独特的构建方式,为图表示学习提供了全新的视角。通过引入多样性因子确保曲率的多样性,以及采用等距的平移不变核层取代传统的指数/对数映射,有效解决了数值稳定性的问题。此外,通过构建自监督的生成对抗模型,MotifRGC成功捕捉了图结构中的模体规律。这些新颖的做法不仅提高了图神经网络的性能,更为复杂结构的图数据的深度学习开辟了新的道路。
实验选择了四个常用的标准图数据集:Cora, Citeseer, Pubmed和Airport。我们将提出的MotifRGC模型与欧式空间中常见的GAT,GCN,SAGE等进行对比和黎曼空间中的SOTA GNN模型进行了对比:1.HGCN:Hyperbolic Graph Convolutional Neural Networks, NIPS192.HGNN:Hyperbolic Graph Neural Networks, NIPS193.LGCN:Lorentzian Graph Convolutional Networks, WWW214.k-GCN:Constant Curvature Graph Convolutional Networks, ICML20.5.H-to-H:A Hyperbolic-to-Hyperbolic Graph Convolutional Network, CVPR21. 6.SelfMG:我们AAAI22的工作7.Q-GCN:Pseudo-Riemannian Graph Convolutional Networks, NIPS22.8.fullyH:Fully Hyperbolic Neural Network, ACL22实验结果充分展示了Diverse-curvature GCN在多个数据集上的出色性能。从实验数据可以看出,无论是在链接预测还是在节点分类任务上,Diverse-curvature GCN都取得了显著的提升。消融实验见原文。对于生成的Motif三角形,我们也进行了研究。具体来说,在GCN的基础上实例化MotifRGC,并通过给定三角形的AUC度量来评估生成的三角形。当三角形的三条边都被正确预测的时候,就认为三角形被正确预测。结果表面,Motif的黎曼流形能够更好的捕获图中Motif的结构。 06.结论Diverse-curvature GCN以其独特的构建方式,为图表示学习提供了全新的视角。通过引入多样性因子确保曲率的多样性,以及采用等距的平移不变核层取代传统的指数/对数映射,有效解决了数值稳定性的问题。此外,通过构建自监督的生成对抗模型,MotifRGC成功捕捉了图结构中的模体规律。这些新颖的做法不仅提高了图神经网络的性能,更为复杂结构的图数据的深度学习开辟了新的道路。