【军事兵棋推演】paper速读：《关于导弹防御系统 (MDS) 的兵棋推演》，哥伦比亚国立大学

【摘 要】 最近，Postnikov 引入了 Bert Kostant 游戏来构建与简单图的二次形式相关的最大正根。这个结果，以及其他一些基于 Cartan 矩阵的游戏，给出了关于代数分类的 Gabriel 定理的新版本。

在本文中，作为 Bert Kostant 游戏的变体，介绍了一种关于导弹防御系统 (MDS) 的兵棋推演。在这种情况下，导弹轨迹被解释为有箭头的合适路径（有向图）。MDS 通过从位于点 (0,0) 的陆基拦截器 (GBI) 发射导弹来保护欧几里得平面的一个区域。在这种情况下，如果与敌军发射相关的适当正数可以写成三角数和平方数的混合和，则导弹成功拦截。

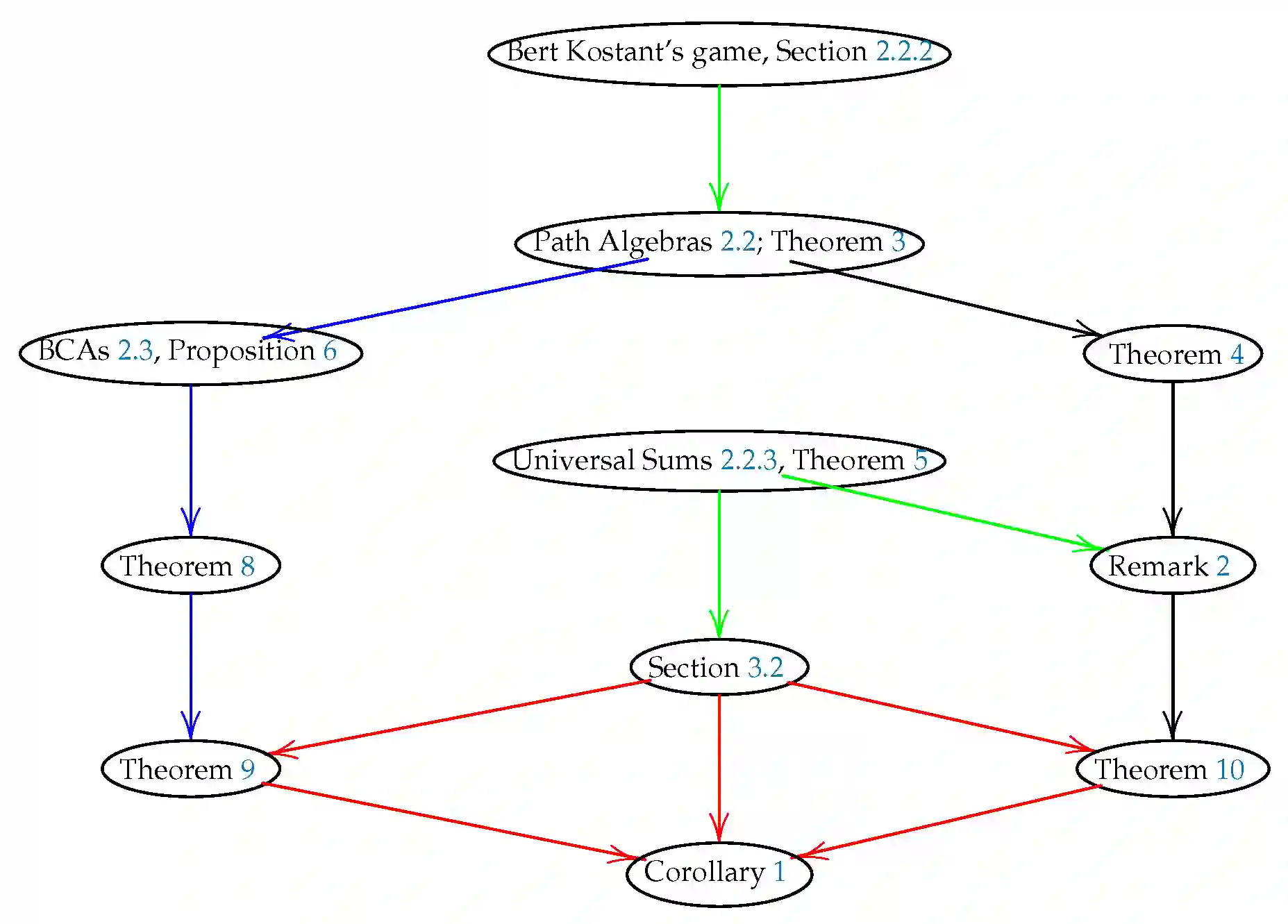
本文结构如下：第 2 节回顾了本文中使用的定义和符号。特别是，回顾了 Bert Kostant 博弈的概念及其一些变体。本节还描述了有关 Brauer 配置代数以及二次形式、这些类型的博弈和路径代数之间的联系。第 3 节给出了主要结果。​定义了一个兵棋推演，其结果基于一些可接受的路径以及三角数和平方数的混合和。结束语和可能的未来工作在第 4 节中描述。

图 1. Brauer 配置代数、Bert Kostant 的博弈以及平方数和三角数的混合和允许在本文中找到主要结果。定理 9 给出了与引入的兵棋推演相关的布劳尔配置代数和相应中心的维数公式。这样的定理允许使用三角数的普遍和来确定地面基地探测器的发射是成功还是未能探测到对手发射的导弹。定理 10 给出了类似的结果，但我们没有使用三角数的全和，而是使用平方数的全和。推论 1 将Legendre–Gauss定理应用于三个平方数之和，以确定哪些条件允许对手在拟议的兵棋推演中取得成功。