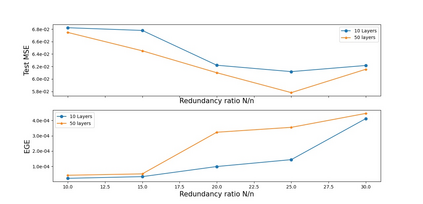
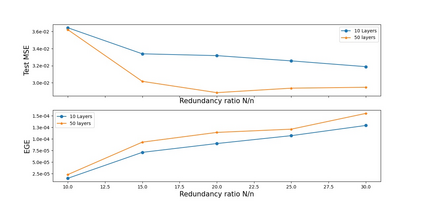
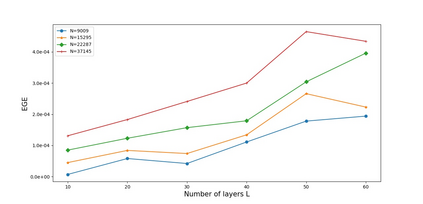
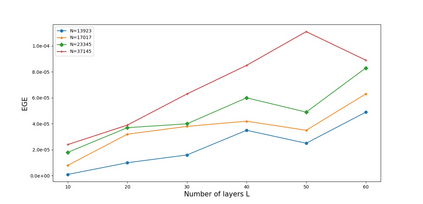
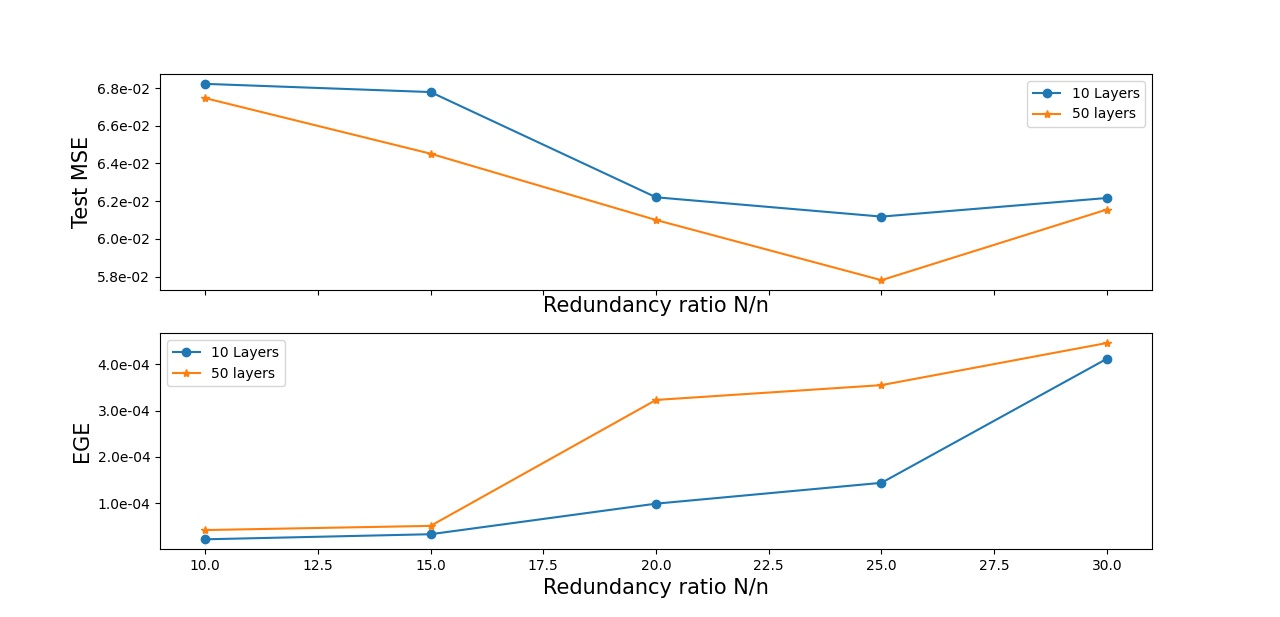
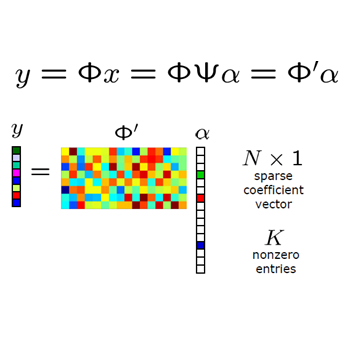
In this paper, we propose a new deep unfolding neural network -- based on a state-of-the-art optimization algorithm -- for analysis Compressed Sensing. The proposed network called Decoding Network (DECONET) implements a decoder that reconstructs vectors from their incomplete, noisy measurements. Moreover, DECONET jointly learns a redundant analysis operator for sparsification, which is shared across the layers of DECONET. We study the generalization ability of DECONET. Towards that end, we first estimate the Rademacher complexity of the hypothesis class consisting of all the decoders that DECONET can implement. Then, we provide generalization error bounds, in terms of the aforementioned estimate. Finally, we present numerical experiments which confirm the validity of our theoretical results.
翻译:在本文中,我们提出一个新的深层发展神经网络 -- -- 以最先进的优化算法为基础 -- -- 用于分析压缩遥感。拟议中的解码网络(DEONET)实施一个解码器,从不完全的、噪音的测量中重建矢量。此外,DEONET共同学习了多余的消音分析操作器,该操作器在DEONET各层之间共享。我们研究了DEONET的普及能力。为此,我们首先估计了DEONET能够实施的所有解码器组成的假设类别 Rademacher的复杂程度。然后,我们提供了上述估计的概括误差。最后,我们提出了数字实验,证实了我们理论结果的有效性。