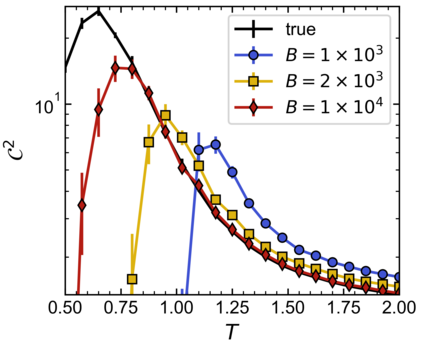
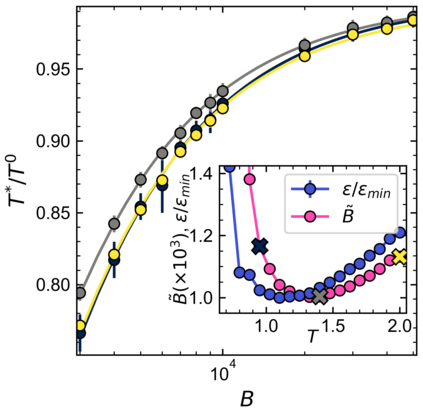
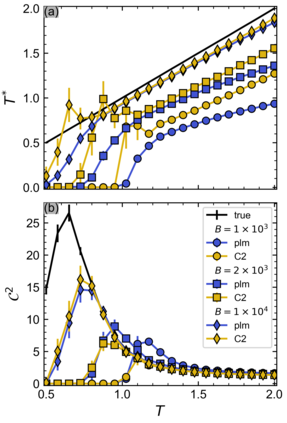
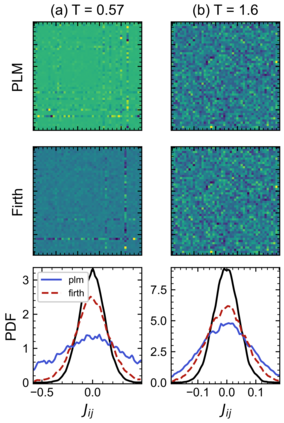
Inverse Ising inference allows pairwise interactions of complex binary systems to be reconstructed from empirical correlations. Typical estimators used for this inference, such as Pseudo-likelihood maximization (PLM), are biased. Using the Sherrington-Kirkpatrick (SK) model as a benchmark, we show that these biases are large in critical regimes close to phase boundaries, and may alter the qualitative interpretation of the inferred model. In particular, we show that the small-sample bias causes models inferred through PLM to appear closer-to-criticality than one would expect from the data. Data-driven methods to correct this bias are explored and applied to a functional magnetic resonance imaging (fMRI) dataset from neuroscience. Our results indicate that additional care should be taken when attributing criticality to real-world datasets.
翻译:反之,推论允许复杂的二进制系统的双向相互作用从经验相关性中重建。 用于这一推论的典型估测者, 如Pseudo- 相似的最大化(PLM), 是有偏向的。 我们用Sherrington- Kirkpatrick (SK) 模型作为基准, 表明这些偏差在接近阶段边界的关键系统中是很大的, 并可能改变对推断模型的定性解释。 特别是, 我们显示, 微小的抽样偏差导致通过PLM 推断的模型看起来比数据预期的更接近临界。 数据驱动的纠正偏差的方法被探索并应用于神经科学的功能磁共振成像(fMRI) 数据集。 我们的结果表明, 当将临界点归结为真实世界数据集时, 需要多加小心。