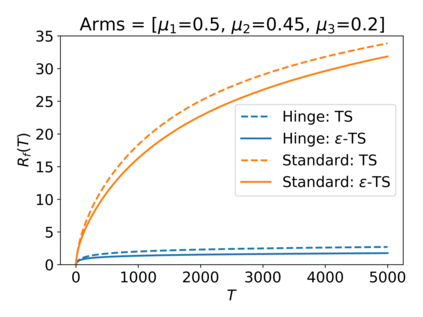
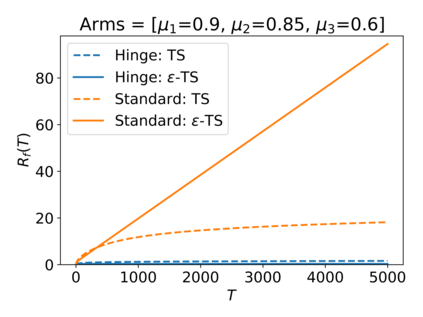
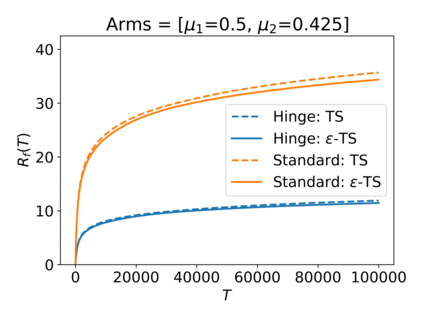
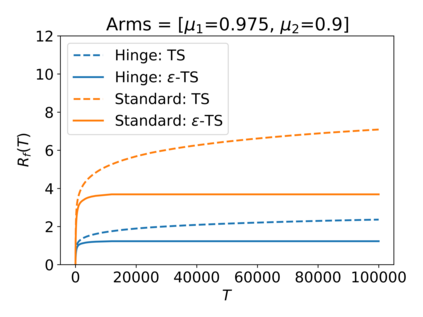
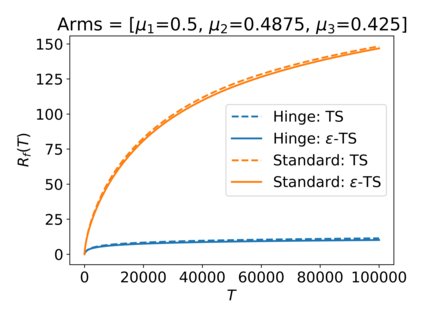
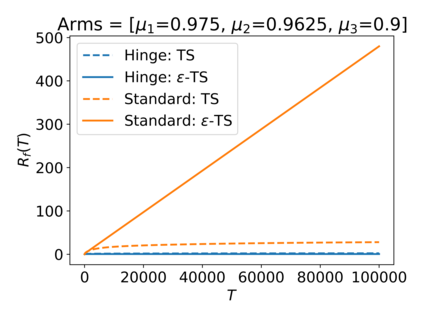
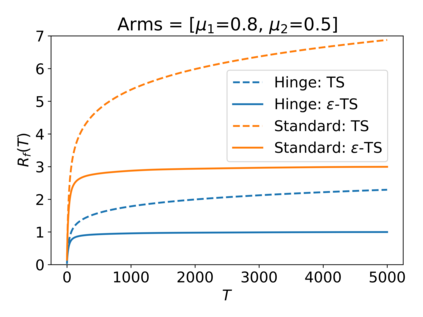
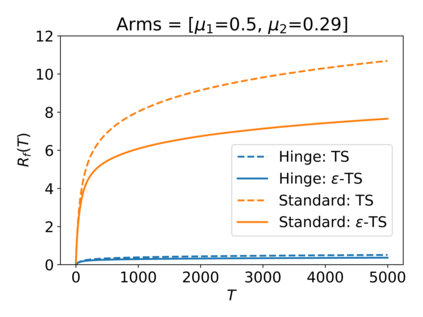
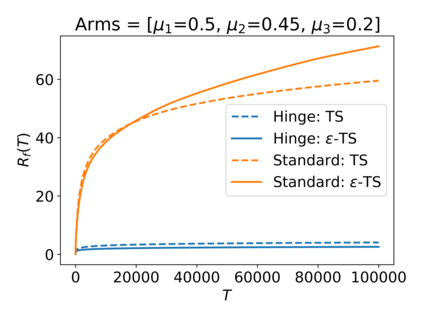
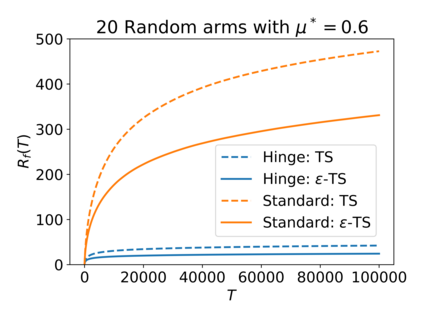
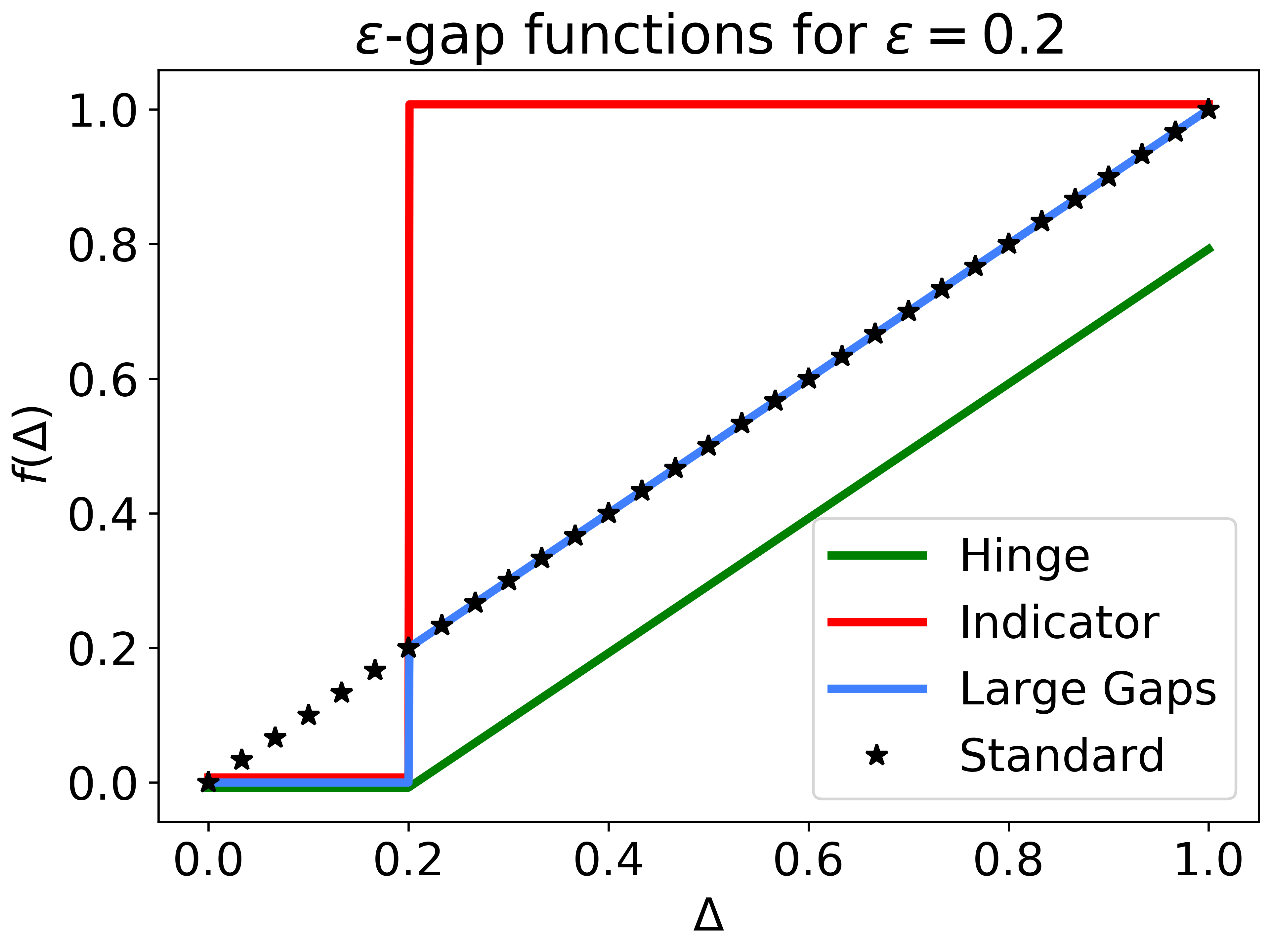
We consider the Multi-Armed Bandit (MAB) problem, where an agent sequentially chooses actions and observes rewards for the actions it took. While the majority of algorithms try to minimize the regret, i.e., the cumulative difference between the reward of the best action and the agent's action, this criterion might lead to undesirable results. For example, in large problems, or when the interaction with the environment is brief, finding an optimal arm is infeasible, and regret-minimizing algorithms tend to over-explore. To overcome this issue, algorithms for such settings should instead focus on playing near-optimal arms. To this end, we suggest a new, more lenient, regret criterion that ignores suboptimality gaps smaller than some $\epsilon$. We then present a variant of the Thompson Sampling (TS) algorithm, called $\epsilon$-TS, and prove its asymptotic optimality in terms of the lenient regret. Importantly, we show that when the mean of the optimal arm is high enough, the lenient regret of $\epsilon$-TS is bounded by a constant. Finally, we show that $\epsilon$-TS can be applied to improve the performance when the agent knows a lower bound of the suboptimality gaps.
翻译:我们认为多武装盗匪(MAB)问题,即一个代理人按顺序选择动作并观察对其所采取行动的奖励。虽然大多数算法试图尽量减少遗憾,即最佳行动的奖励与代理人行动之间的累积差差,但这一标准可能导致不良结果。例如,在大问题中,或当与环境的互动很短暂时,找到一个最佳手臂是不可行的,而遗憾最小化的算法往往会过度爆炸。为了克服这一问题,这种环境的算法应该侧重于玩近最佳的手臂。为此,我们建议采用新的、更宽容的、更遗憾的标准,忽略比某些美元小的次优性差距。然后我们提出一个汤普森Smpling(TS)算法的变式,称为$epslon-TS, 并证明它从宽度的角度来说是无差别的。重要的是,当我们最佳手臂的平均值足够高的时候, $\epslon-plon-TS最终能够显示一个稳定的副动作。