On concordance indices for models with time-varying risk

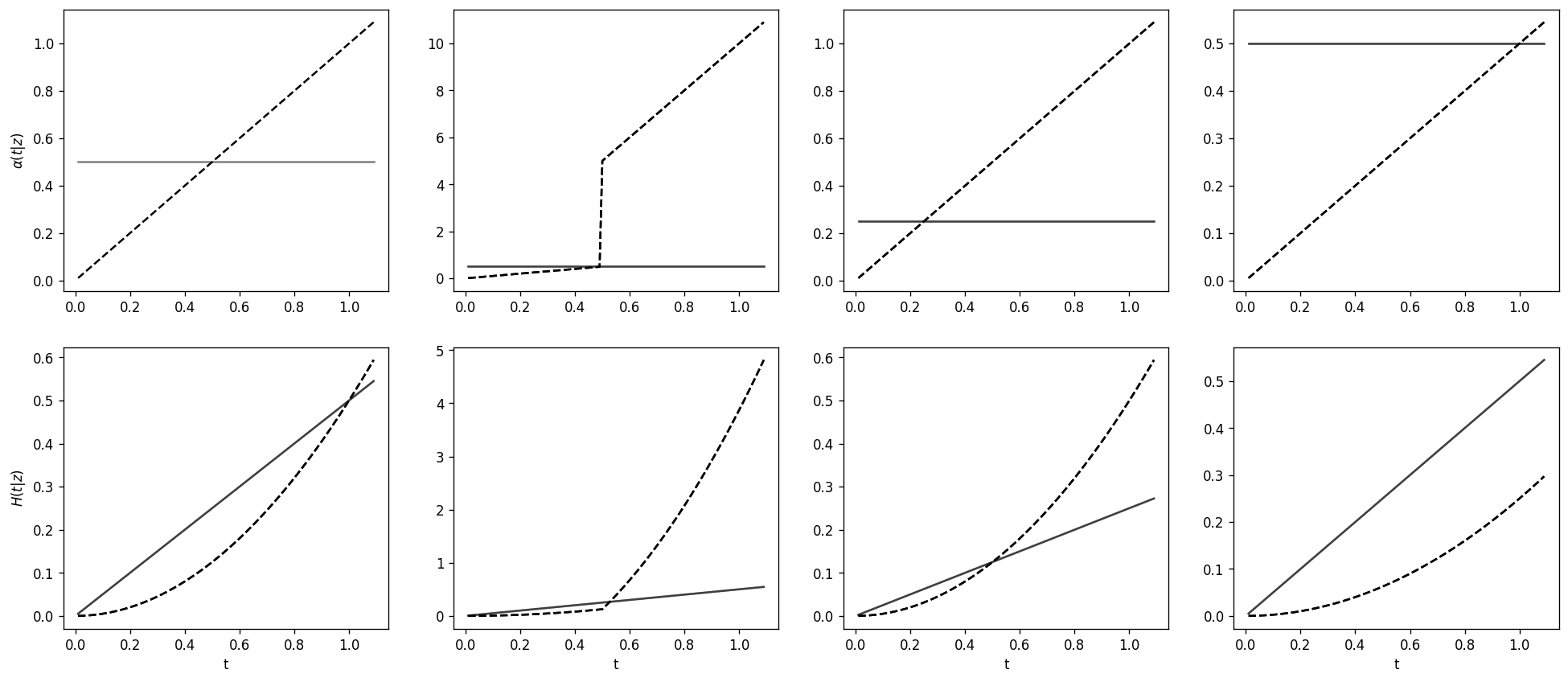
Harrel's concordance index is a commonly used discrimination metric for survival models, particularly for models where the relative ordering of the risk of individuals is time-independent, such as the proportional hazards model. There are several suggestions, but no consensus, on how it could be extended to models where risk varies over time, e.g.\ in case of crossing hazard rates. We show that, in the limit, concordance is maximized if and only if the risk score is concordant with the hazard rate, in the sense that for a comparable pair where the first event time is observed, the risk score is concordant with the hazard rate at this first event time. Thus, we suggest using the hazard rate as the risk score when calculating concordance. Through simulations, we demonstrate situations in which other concordance indices can lead to incorrect models being selected over a true model, justifying the use of our suggested risk prediction in both model selection and in loss functions in, e.g., machine learning models.