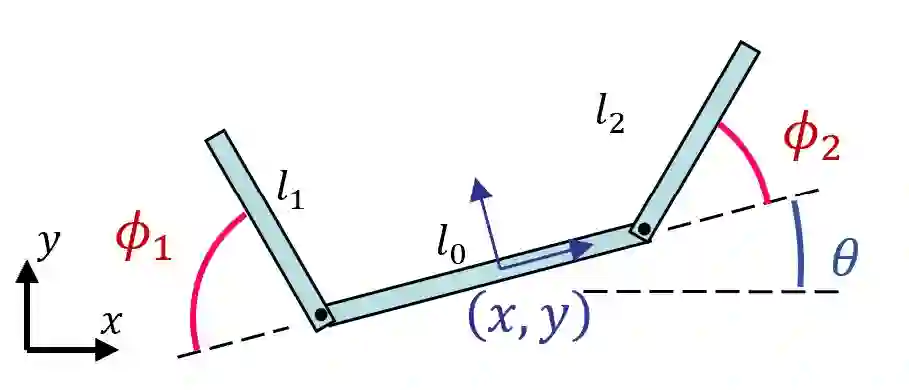
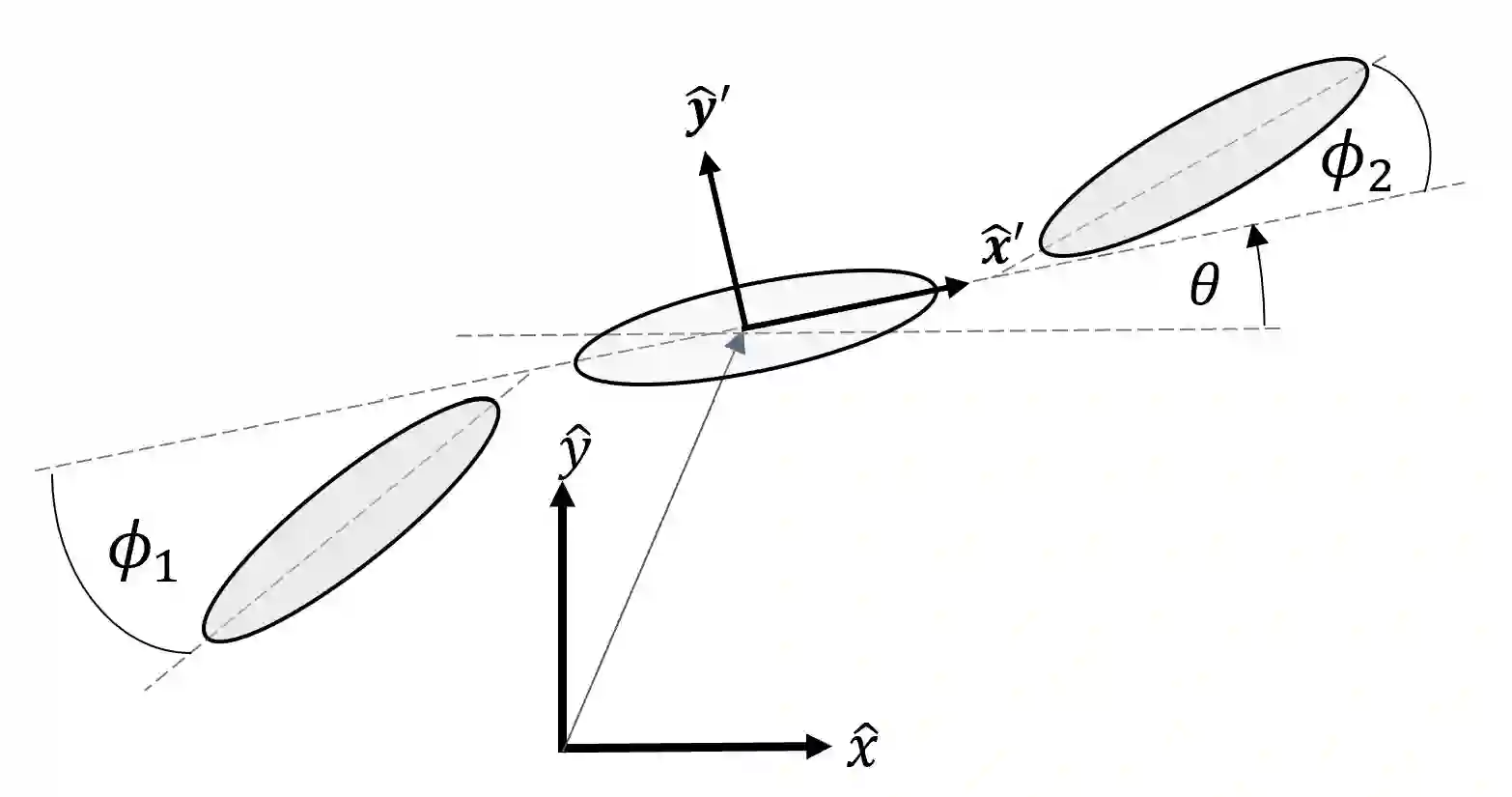
Many robotic systems locomote using gaits - periodic changes of internal shape, whose mechanical interaction with the robot`s environment generate characteristic net displacements. Prominent examples with two shape variables are the low Reynolds number 3-link "Purcell swimmer" with inputs of 2 joint angles and the "ideal fluid" swimmer. Gait analysis of these systems allows for intelligent decisions to be made about the swimmer`s locomotive properties, increasing the potential for robotic autonomy. In this work, we present comparative analysis of gait optimization using two different methods. The first method is variational approach of "Pontryagin`s maximum principle" (PMP) from optimal control theory. We apply PMP for several variants of 3-link swimmers, with and without incorporation of bounds on joint angles. The second method is differential-geometric analysis of the gaits based on curvature (total Lie bracket) of the local connection for 3-link swimmers. Using optimized body-motion coordinates, contour plots of the curvature in shape space gives visualization that enables identifying distance-optimal gaits as zero level sets. Combining and comparing results of the two methods enables better understanding of changes in existence, shape and topology of distance-optimal gait trajectories, depending on the swimmers' parameters.
翻译:许多机器人系统使用轨迹 -- -- 内部形状定期变化,其机械与机器人环境的机械互动产生典型的净置换。有两个形状变量的突出实例是低 Reynolds 3-link “Purcell 游泳器”,输入两个联合角度和“理想液体”游泳器。对这些系统的盖特分析允许对游泳机的机车特性作出明智的决定,增加机器人自主的潜力。在这项工作中,我们使用两种不同的方法对运动优化进行比较分析。第一个方法是从最佳控制理论中“Pontryagin`s 最高原理”(PMP) 的变异式方法。我们应用了3-link游泳器的若干变式“Purcell 游泳器”, 输入了两个共同角度, 并且没有将“理想” 水手动。第二个方法是根据三链接游泳机的曲线(全部隐蔽层) 来对阵容进行差别地分析。我们使用两种不同的方法对运动优化的体姿势坐标、轮廓的轮廓图图图图进行比较分析。从最佳控制理论中可视化两种方法可以辨辨辨辨测出远距离的阵形阵势,从而得以辨辨测出空间的面面面面面面面面面面面面面面面面面面面面面面面面面面面图,使模型的图像的模型化方法,使对面面面面面面面面面面面面面面图的模型的形状的形状的形状的形状的形状的形状得以比较,使对面的形状的形状的形状的形状的形状的形状的形状进行比较,使对面图,使对面的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状进行比较,使对面观测为为零的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状进行。制,使,使使使能,使能法的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形态的形态的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状的形状得以比较。