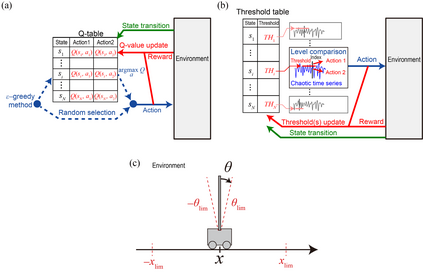
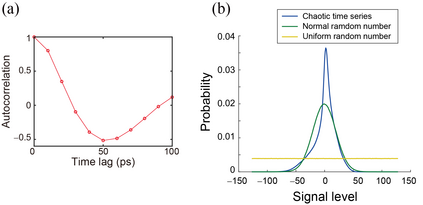
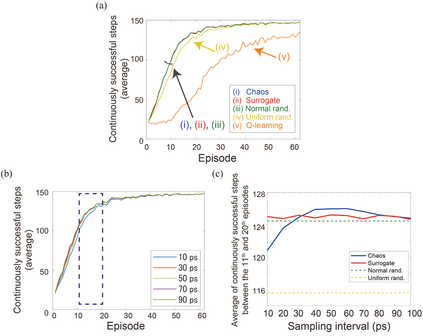
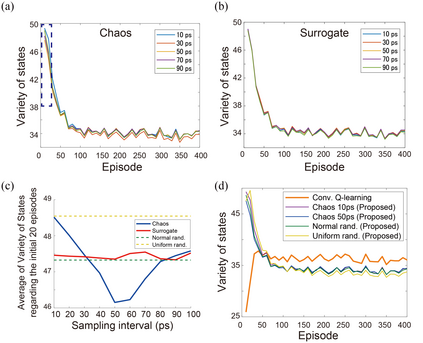
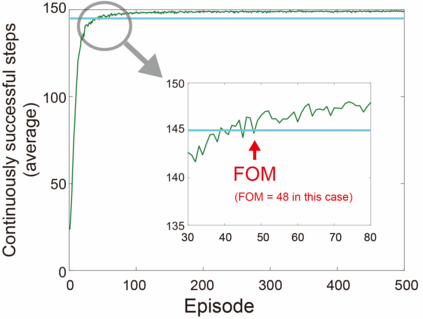
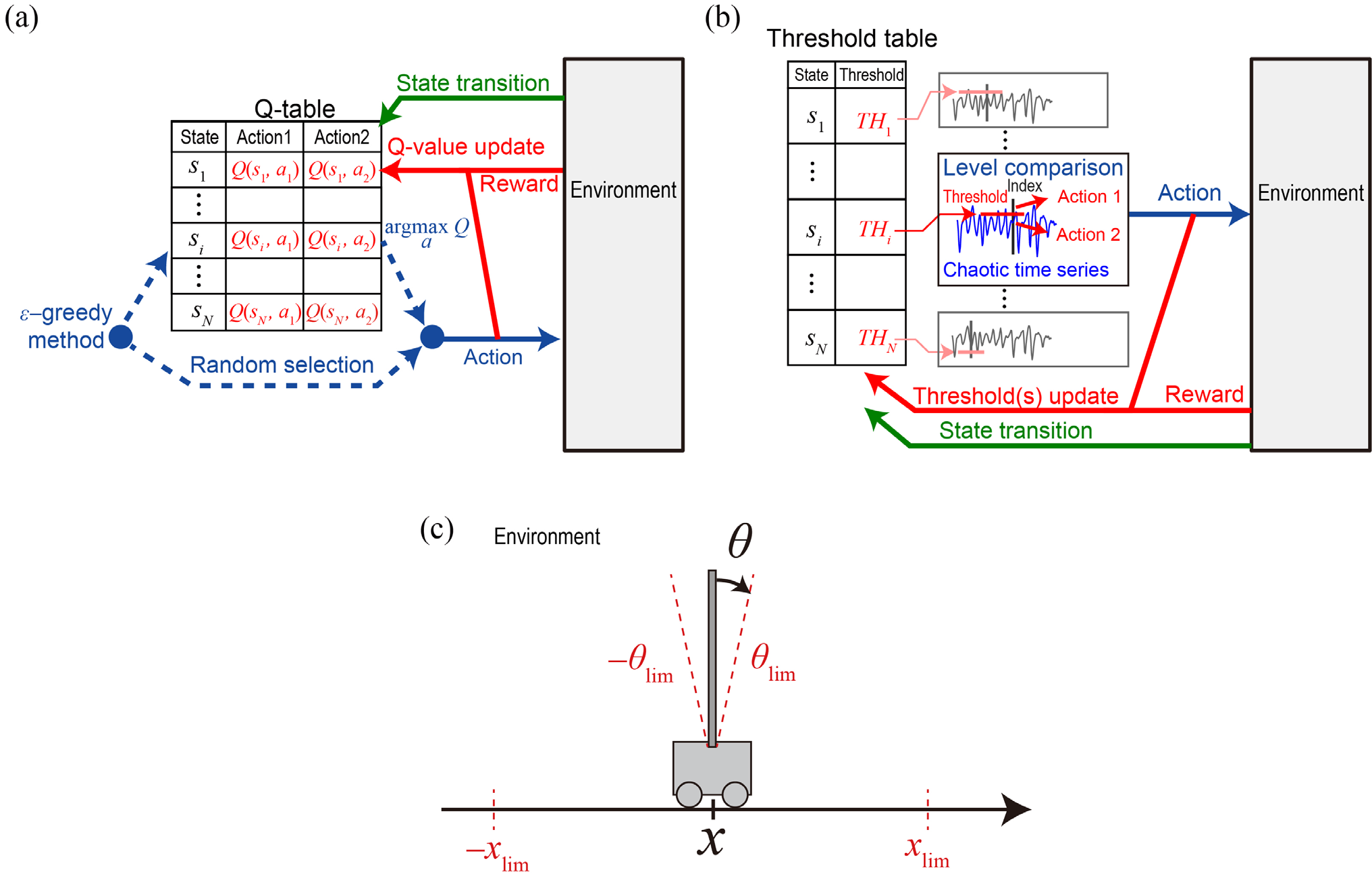
Accelerating artificial intelligence by photonics is an active field of study aiming to exploit the unique properties of photons. Reinforcement learning is an important branch of machine learning, and photonic decision-making principles have been demonstrated with respect to the multi-armed bandit problems. However, reinforcement learning could involve a massive number of states, unlike previously demonstrated bandit problems where the number of states is only one. Q-learning is a well-known approach in reinforcement learning that can deal with many states. The architecture of Q-learning, however, does not fit well photonic implementations due to its separation of update rule and the action selection. In this study, we organize a new architecture for multi-state reinforcement learning as a parallel array of bandit problems in order to benefit from photonic decision-makers, which we call parallel bandit architecture for reinforcement learning or PBRL in short. Taking a cart-pole balancing problem as an instance, we demonstrate that PBRL adapts to the environment in fewer time steps than Q-learning. Furthermore, PBRL yields faster adaptation when operated with a chaotic laser time series than the case with uniformly distributed pseudorandom numbers where the autocorrelation inherent in the laser chaos provides a positive effect. We also find that the variety of states that the system undergoes during the learning phase exhibits completely different properties between PBRL and Q-learning. The insights obtained through the present study are also beneficial for existing computing platforms, not just photonic realizations, in accelerating performances by the PBRL algorithms and correlated random sequences.
翻译:光子加速人工智能是一个积极的研究领域,目的是利用光子的独特性能。强化学习是机器学习的一个重要分支,在多武装土匪问题方面,已经展示了光度决策原则。然而,强化学习可能涉及大量国家,不同于以前所显示的只有一个国家的土匪问题。Q学习是一个众所周知的加强学习的方法,它可以与许多国家打交道。但是,由于Q学习的结构将更新规则与行动选择分开,因此不适合光度执行。在本研究中,我们组织了一个新的结构,将多州强化学习作为平行的土匪问题系列,以平行的土匪问题来学习。然而,我们称之为平行的土匪学习结构,不同于先前所显示的土匪问题,因为国家数目只有一个。用木质平衡问题的方法来强化学习,我们证明PBRL的架构与环境的随机适应速度不及光度不相匹配。此外,PBRLL的架构在操作一个混乱的激光时间序列中产生更快的适应性能。 QQQ,我们组织了一个平行分布式的混凝度的混杂的模拟学习模型,我们也可以通过不同阶段的变的变的变的自我理解, 。