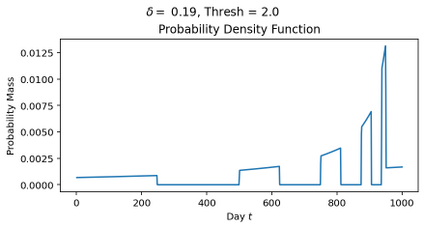
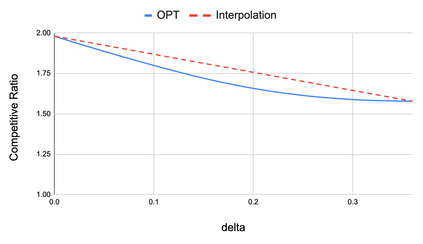
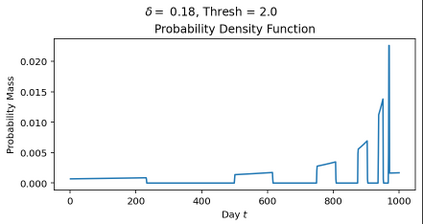
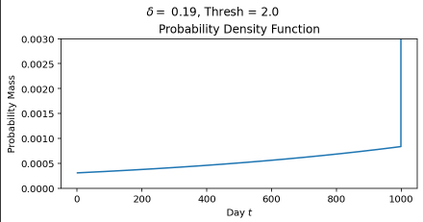
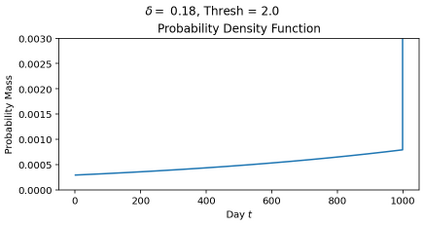
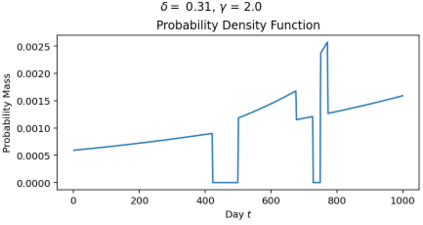
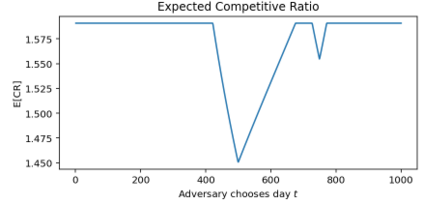
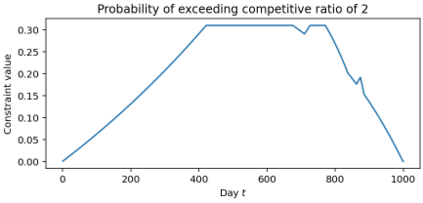
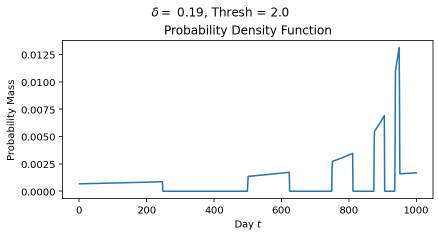
The classical ski-rental problem admits a textbook 2-competitive deterministic algorithm, and a simple randomized algorithm that is $\frac{e}{e-1}$-competitive in expectation. The randomized algorithm, while optimal in expectation, has a large variance in its performance: it has more than a 37% chance of competitive ratio exceeding 2, and a $\Theta(1/n)$ chance of the competitive ratio exceeding $n$! We ask what happens to the optimal solution if we insist that the tail risk, i.e., the chance of the competitive ratio exceeding a specific value, is bounded by some constant $\delta$. We find that this additional modification significantly changes the structure of the optimal solution. The probability of purchasing skis on a given day becomes non-monotone, discontinuous, and arbitrarily large (for sufficiently small tail risk $\delta$ and large purchase cost $n$).
翻译:暂无翻译