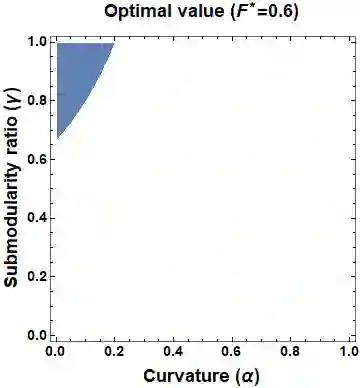
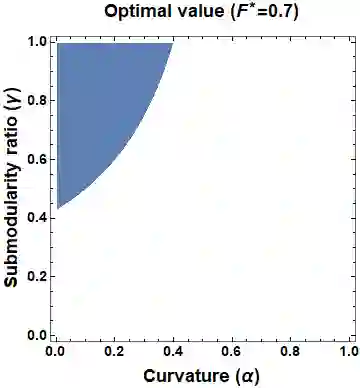
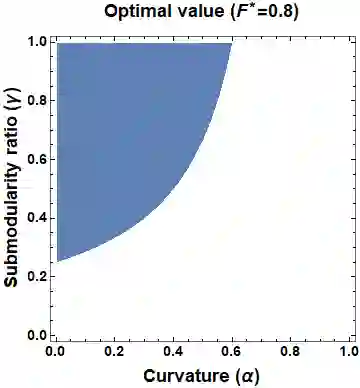
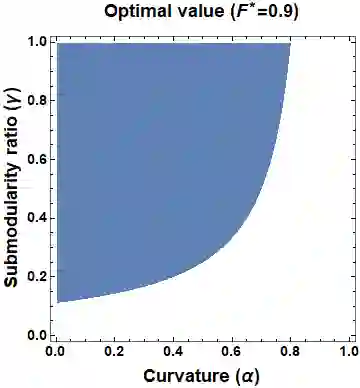
This paper considers the problem of multi-robot safe mission planning in uncertain dynamic environments. This problem arises in several applications including safety-critical exploration, surveillance, and emergency rescue missions. Computation of a multi-robot optimal control policy is challenging not only because of the complexity of incorporating dynamic uncertainties while planning, but also because of the exponential growth in problem size as a function of number of robots. Leveraging recent works obtaining a tractable safety maximizing plan for a single robot, we propose a scalable two-stage framework to solve the problem at hand. Specifically, the problem is split into a low-level single-agent planning problem and a high-level task allocation problem. The low-level problem uses an efficient approximation of stochastic reachability for a Markov decision process to handle the dynamic uncertainty. The task allocation, on the other hand, is solved using polynomial-time forward and reverse greedy heuristics. The multiplicative safety objective of our multi-robot safe planning problem allows decoupling in order to implement the greedy heuristics through a distributed auction-based approach. Moreover, by leveraging the properties of this safety objective function, we ensure provable performance bounds on the safety of the approximate solutions proposed by these two heuristics.
翻译:本文探讨了在不确定的动态环境中多机器人安全飞行任务规划的问题。 这个问题出现在几个应用中, 包括安全临界勘探、 监视和紧急救援任务。 计算多机器人最佳控制政策具有挑战性, 不仅因为在规划过程中纳入动态不确定性的复杂性, 而且还因为由于机器人数目的函数作用而使问题规模成指数增长。 利用最新作品为单一机器人获得可移植安全最大化计划的可能性, 我们提议了一个可扩展的两阶段框架来解决手头的问题。 具体地说, 问题被分为一个低层次的单一代理人规划问题和一个高层次的任务分配问题。 低层次问题使用高效的随机可达性近似马尔科夫决策程序来处理动态不确定性。 另一方面, 任务分配是使用多元时前和倒向贪婪的超自然论。 我们多机器人安全规划问题的多复制性安全目标可以分解, 以便通过分散的拍卖方法实施贪婪的超自然安全性。 此外, 利用这一目标性功能的稳妥性。