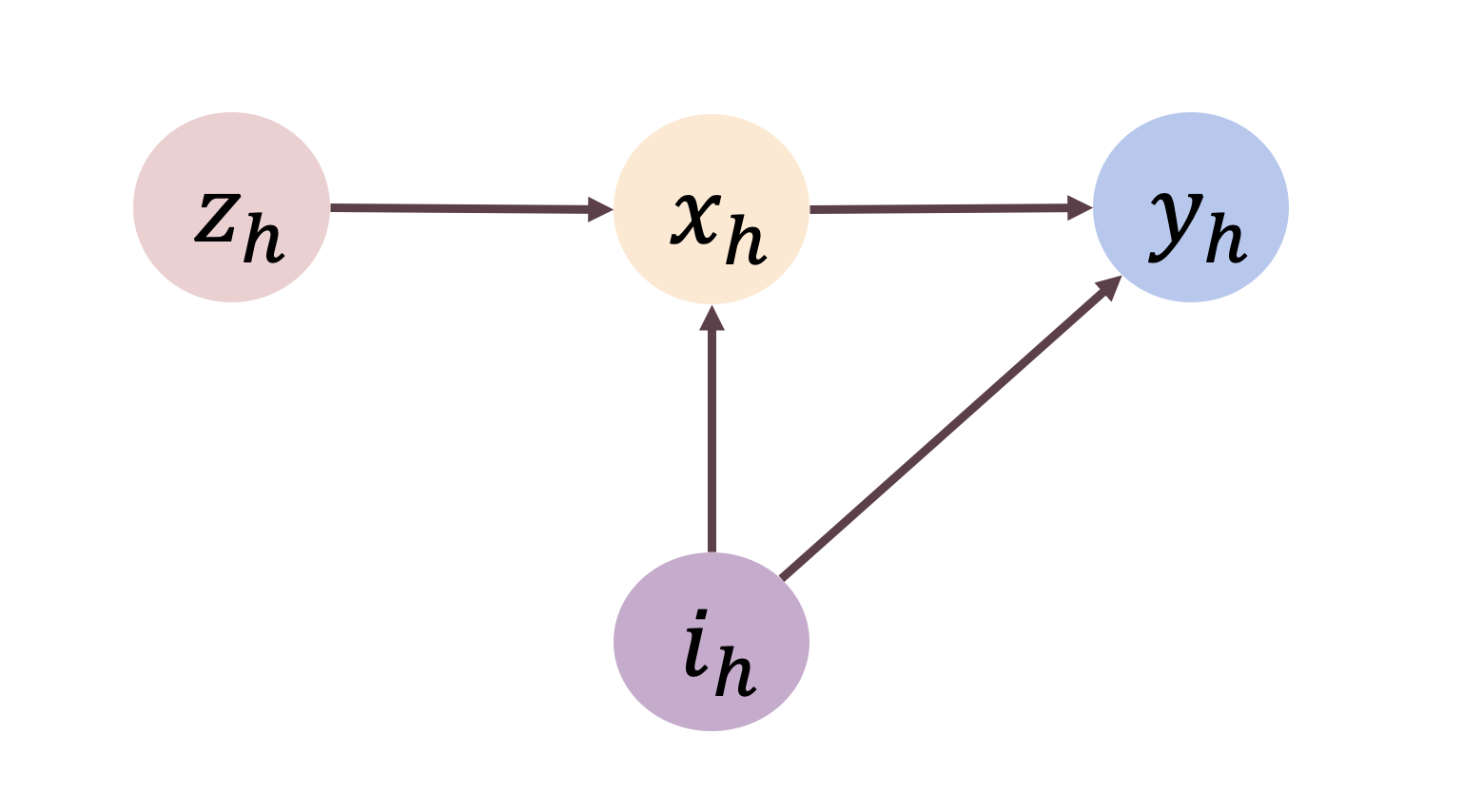
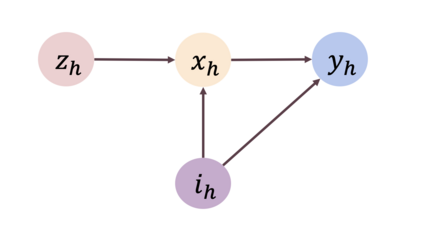
We study offline reinforcement learning under a novel model called strategic MDP, which characterizes the strategic interactions between a principal and a sequence of myopic agents with private types. Due to the bilevel structure and private types, strategic MDP involves information asymmetry between the principal and the agents. We focus on the offline RL problem, where the goal is to learn the optimal policy of the principal concerning a target population of agents based on a pre-collected dataset that consists of historical interactions. The unobserved private types confound such a dataset as they affect both the rewards and observations received by the principal. We propose a novel algorithm, Pessimistic policy Learning with Algorithmic iNstruments (PLAN), which leverages the ideas of instrumental variable regression and the pessimism principle to learn a near-optimal principal's policy in the context of general function approximation. Our algorithm is based on the critical observation that the principal's actions serve as valid instrumental variables. In particular, under a partial coverage assumption on the offline dataset, we prove that PLAN outputs a $1 / \sqrt{K}$-optimal policy with $K$ being the number of collected trajectories. We further apply our framework to some special cases of strategic MDP, including strategic regression, strategic bandit, and noncompliance in recommendation systems.
翻译:我们在一个名为战略MDP的新模式下研究脱线强化学习,这个新模式被称为战略MDP,是一流和一连串私人类型的近亲代理人之间的战略互动的特点。由于双层结构和私人类型,战略MDP涉及主要代理人和代理人之间的信息不对称。我们侧重于脱线RL问题,在脱线RL问题上,我们的目标是根据由历史互动构成的预先收集数据集,了解本部对代理人目标人群的最佳政策。未观测的私人类型混淆了这样一个数据集,因为它们既影响本部收到的奖赏和意见。我们提议了一个新奇的算法,即与阿尔高思米电子结构的悲观政策学习(PLAN),利用工具变量回归和悲观原则的概念,在一般功能接近的背景下学习近于最佳的本部政策。我们的算法基于关键观察,即本部的行动是有效的工具变量。在离线数据集的部分覆盖假设下,我们证明计划产生了1/sqrt{K$/koff 和我们的一些战略回归框架,包括我们所收集的战略案例。