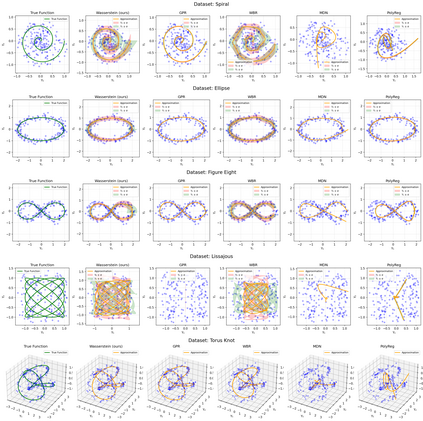
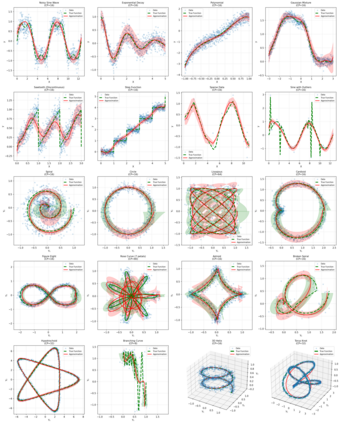
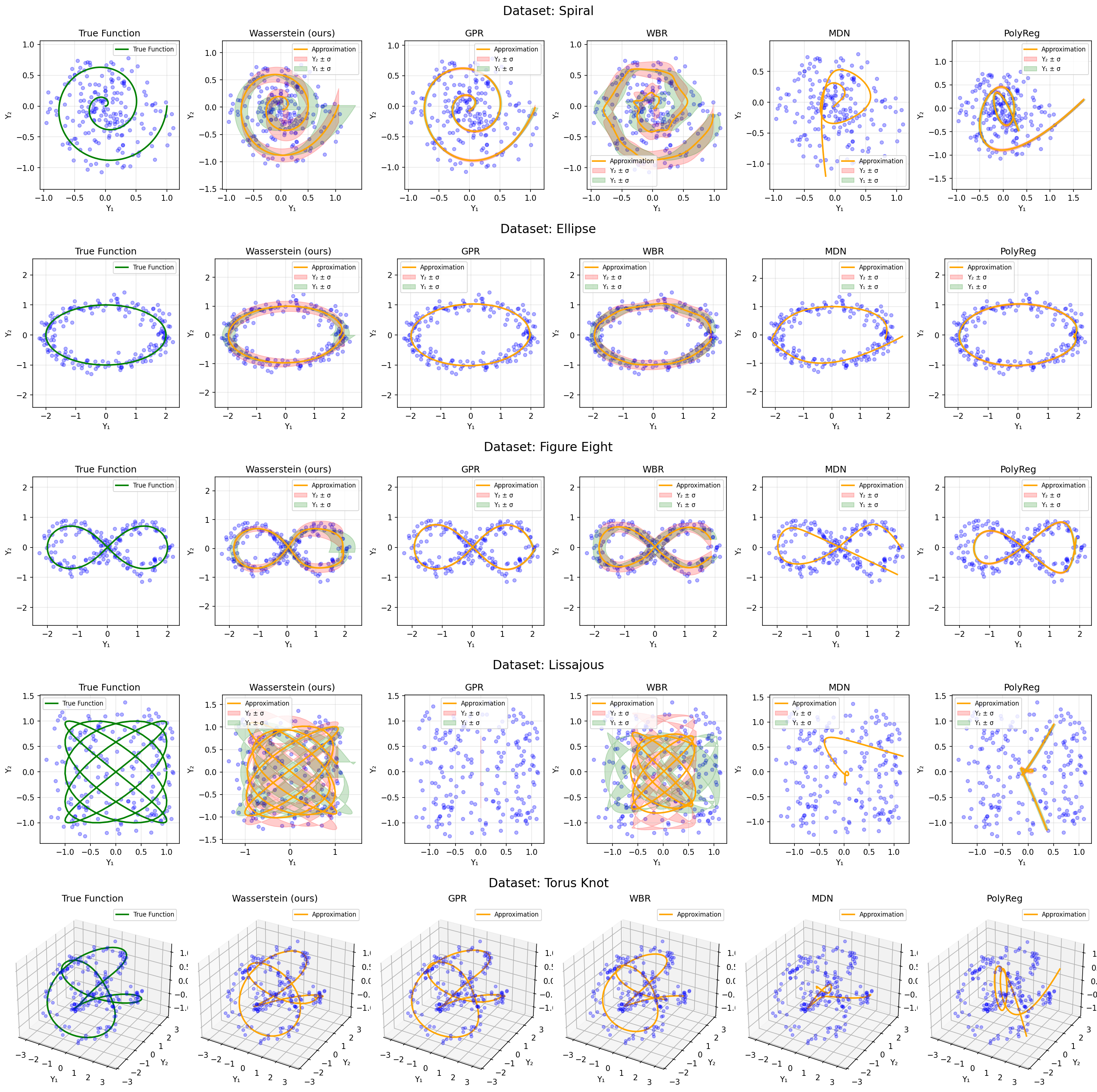
This paper considers the problem of regression over distributions, which is becoming increasingly important in machine learning. Existing approaches often ignore the geometry of the probability space or are computationally expensive. To overcome these limitations, a new method is proposed that combines the parameterization of probability trajectories using a Bernstein basis and the minimization of the Wasserstein distance between distributions. The key idea is to model a conditional distribution as a smooth probability trajectory defined by a weighted sum of Gaussian components whose parameters -- the mean and covariance -- are functions of the input variable constructed using Bernstein polynomials. The loss function is the averaged squared Wasserstein distance between the predicted Gaussian distributions and the empirical data, which takes into account the geometry of the distributions. An autodiff-based optimization method is used to train the model. Experiments on synthetic datasets that include complex trajectories demonstrated that the proposed method provides competitive approximation quality in terms of the Wasserstein distance, Energy Distance, and RMSE metrics, especially in cases of pronounced nonlinearity. The model demonstrates trajectory smoothness that is better than or comparable to alternatives and robustness to changes in data structure, while maintaining high interpretability due to explicit parameterization via control points. The developed approach represents a balanced solution that combines geometric accuracy, computational practicality, and interpretability. Prospects for further research include extending the method to non-Gaussian distributions, applying entropy regularization to speed up computations, and adapting the approach to working with high-dimensional data for approximating surfaces and more complex structures.
翻译:暂无翻译