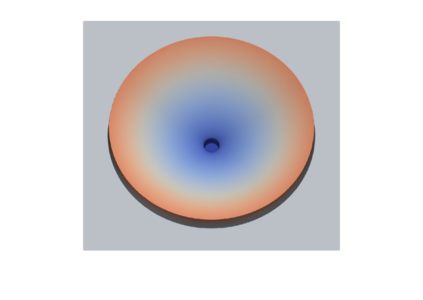
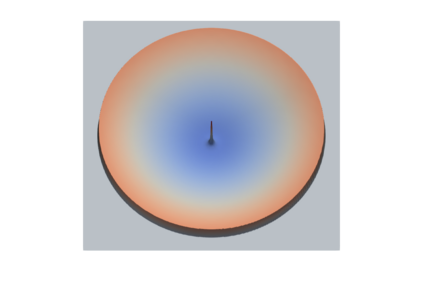
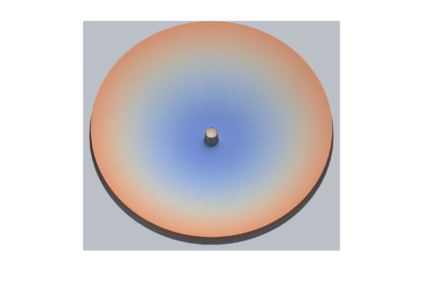
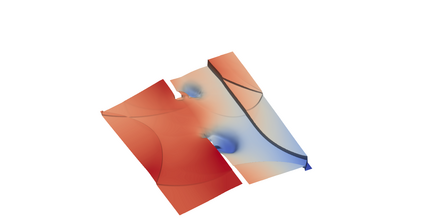
A quasi-second order scheme is developed to obtain approximate solutions of the shallow water equationswith bathymetry. The scheme is based on a staggered finite volume scheme for the space discretization:the scalar unknowns are located in the discretisation cells while the vector unknowns are located on theedges (in 2D) or faces (in 3D) of the mesh. A MUSCL-like interpolation for the discrete convectionoperators in the water height and momentum equations is performed in order to improve the precisionof the scheme. The time discretization is performed either by a first order segregated forward Eulerscheme in time or by the second order Heun scheme. Both schemes are shown to preserve the waterheight positivity under a CFL condition and an important state equilibrium known as the lake at rest.Using some recent Lax-Wendroff type results for staggered grids, these schemes are shown to be Lax-consistent with the weak formulation of the continuous equations; besides, the forward Euler schemeis shown to be consistent with a weak entropy inequality. Numerical results confirm the efficiency andaccuracy of the schemes.
翻译:为获得浅水方程和测深法的近似解决办法,制定了一个准第二顺序方案,以获得浅水方程的近似解决办法。这个方案基于空间离散的交错定量量办法:卡路里未知物位于离散细胞中,而矢量未知物位于网格的边缘(在2D)或面部(在3D)上。在水高度和动力方程中,对离散的对流者进行了类似于MUSCL的内插,以提高这一办法的精确性。时间离散要么是按时间或按Heun办法的第二个顺序排列的。这两种办法都显示在CFL状态下保持水位率的假设性,另一个重要的状态平衡被称为休息时的湖泊。Using最近一些拉克斯-Wendroff类型的对断格子结果显示,这些办法与持续方程的微变形一致;此外,前Euler方案显示与薄弱的encregreal方案一致。