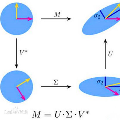
We introduce and investigate matrix approximation by decomposition into a sum of radial basis function (RBF) components. An RBF component is a generalization of the outer product between a pair of vectors, where an RBF function replaces the scalar multiplication between individual vector elements. Even though the RBF functions are positive definite, the summation across components is not restricted to convex combinations and allows us to compute the decomposition for any real matrix that is not necessarily symmetric or positive definite. We formulate the problem of seeking such a decomposition as an optimization problem with a nonlinear and non-convex loss function. Several modern versions of the gradient descent method, including their scalable stochastic counterparts, are used to solve this problem. We provide extensive empirical evidence of the effectiveness of the RBF decomposition and that of the gradient-based fitting algorithm. While being conceptually motivated by singular value decomposition (SVD), our proposed nonlinear counterpart outperforms SVD by drastically reducing the memory required to approximate a data matrix with the same L2 error for a wide range of matrix types. For example, it leads to 2 to 6 times memory save for Gaussian noise, graph adjacency matrices, and kernel matrices. Moreover, this proximity-based decomposition can offer additional interpretability in applications that involve, e.g., capturing the inner low-dimensional structure of the data, retaining graph connectivity structure, and preserving the acutance of images.
翻译:通过分解成一条辐射基函数(RBF)的组合,我们引入和调查矩阵近似。RBF组件是一对矢量之间外产产品的概括化,其中RBF函数取代了各个矢量元素之间的伸缩乘法。尽管RBF函数是肯定的,但各组成部分之间的相加并不局限于混和组合,使我们能够计算任何并不一定对称或正数真实矩阵的分解。我们把寻求这种分解作为非线性和非对流性功能损失结构的最优化问题提出来。使用几种现代的梯度回溯方法,包括可伸缩的对等功能来解决这个问题。我们提供了大量的经验证据,说明RBFF的分解和基于梯度的调算法的有效性。我们提议的非线性对口方在概念上受到单值分解(SVD)的驱动,我们提议的非直线性直径直径直的对口方在SVD上进行分解,我们大幅减少所需的记忆,以近似的e2级和L2级图像的缩缩缩缩缩缩图, 提供了一系列的缩略数据。