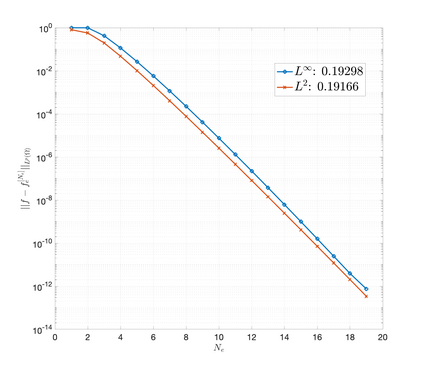
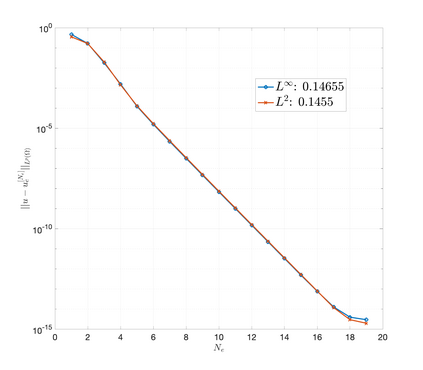
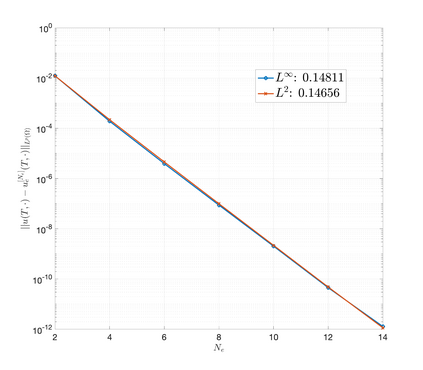
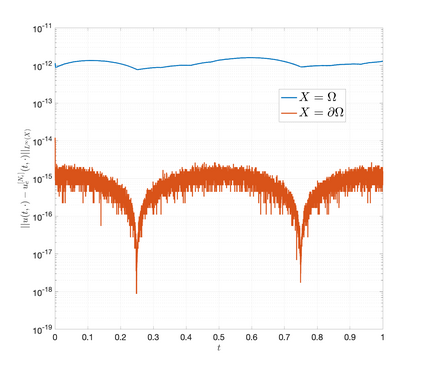
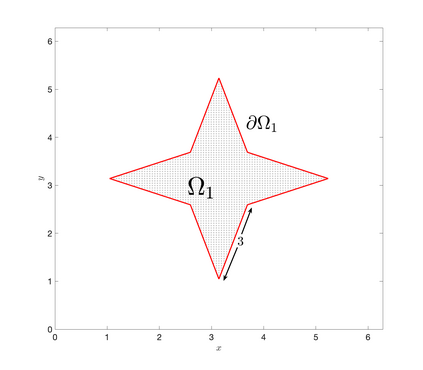
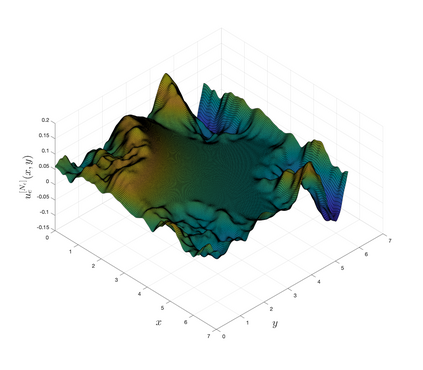
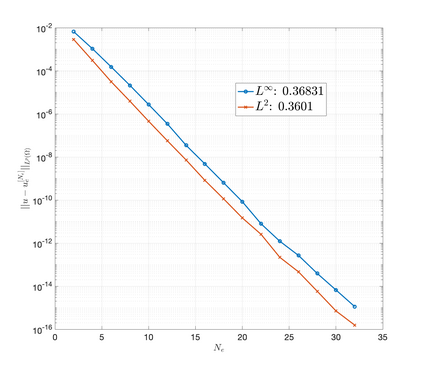
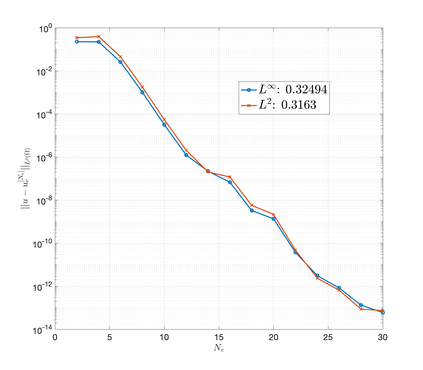
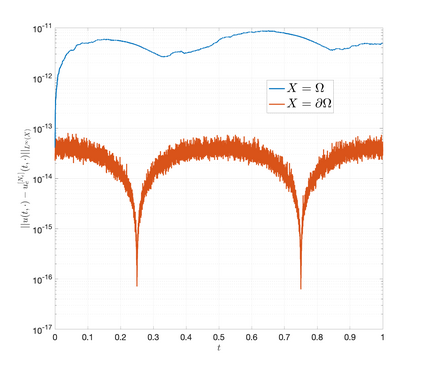
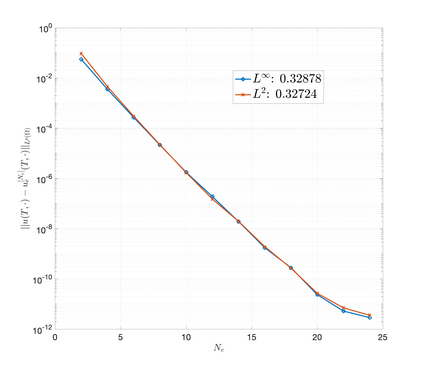
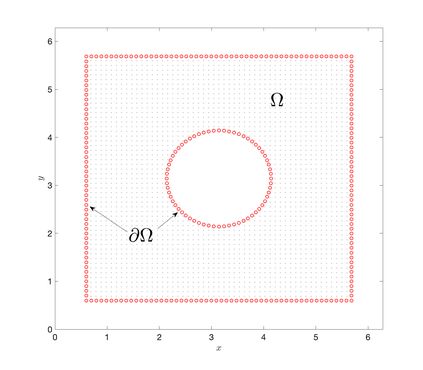
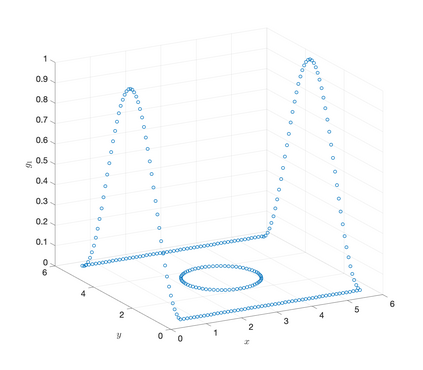
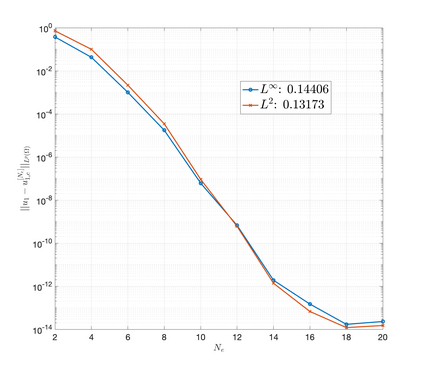
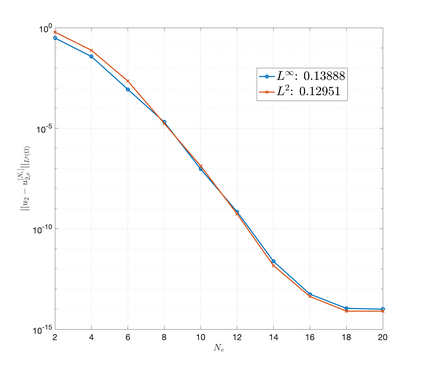
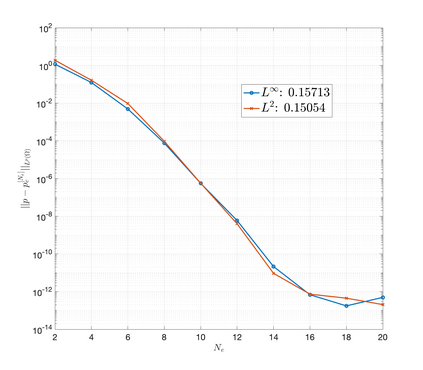
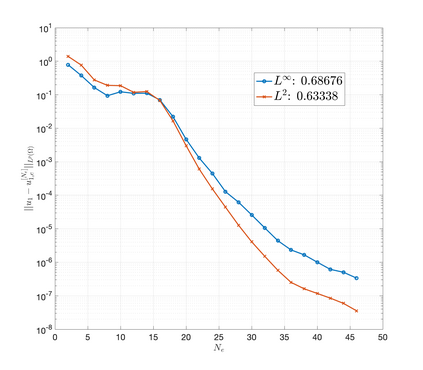
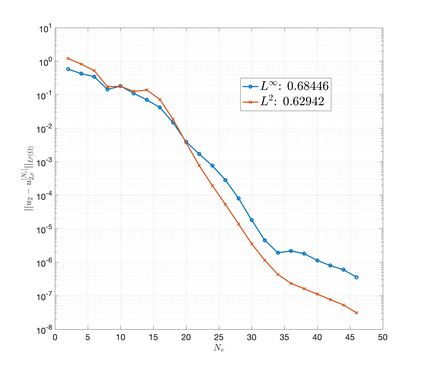
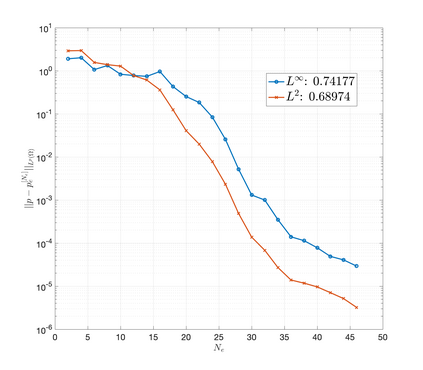
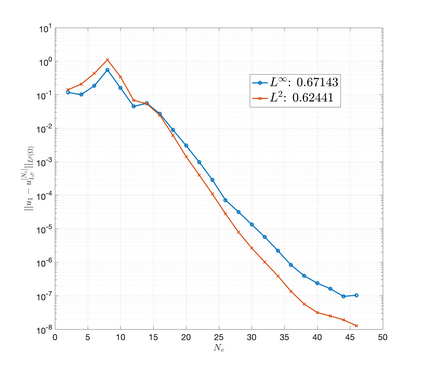
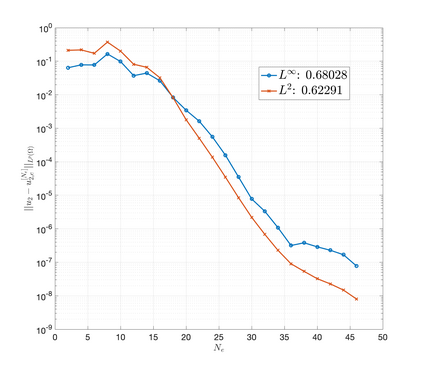
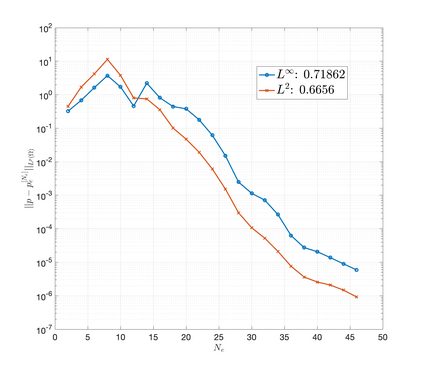
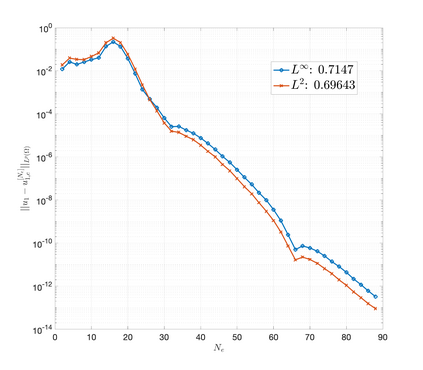
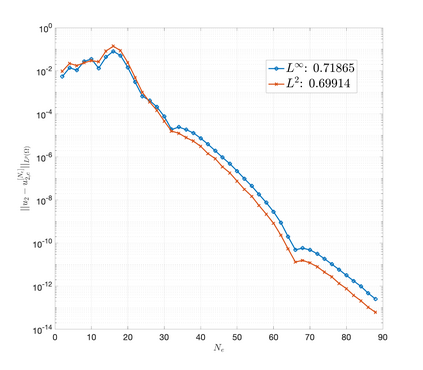
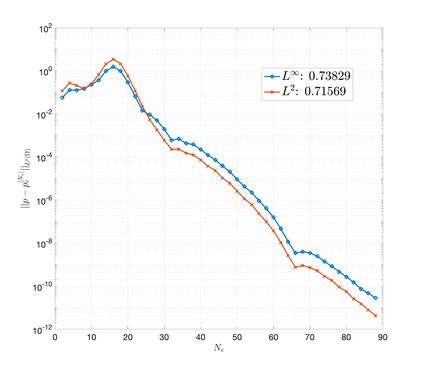
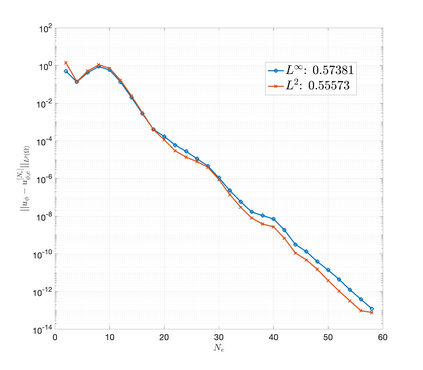
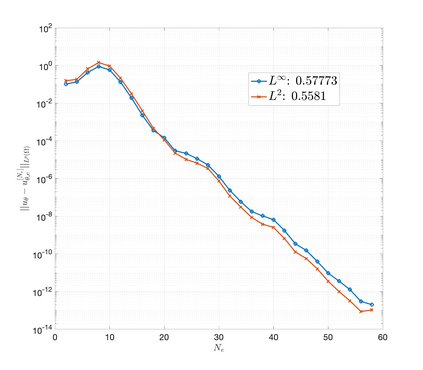
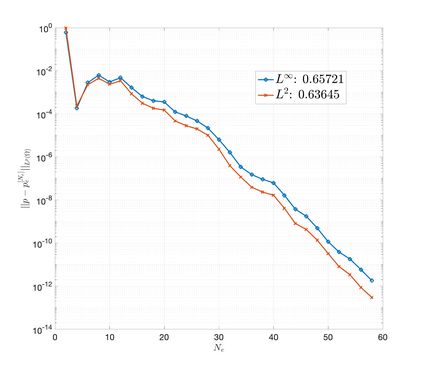
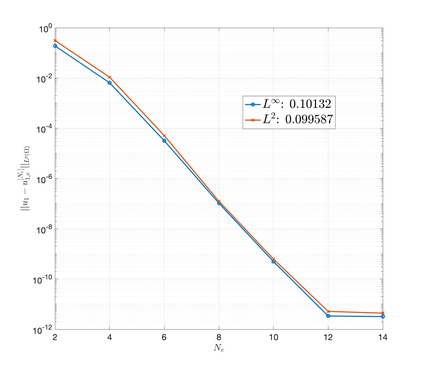
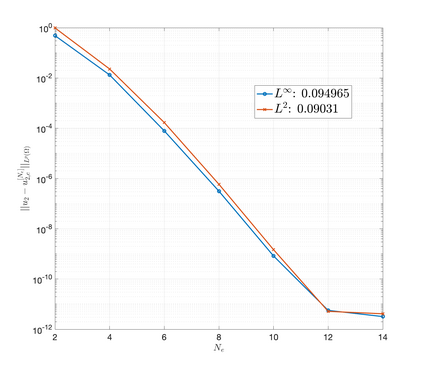
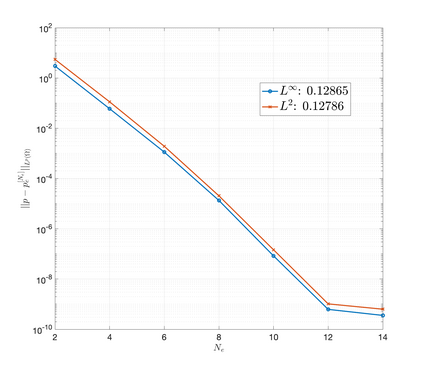
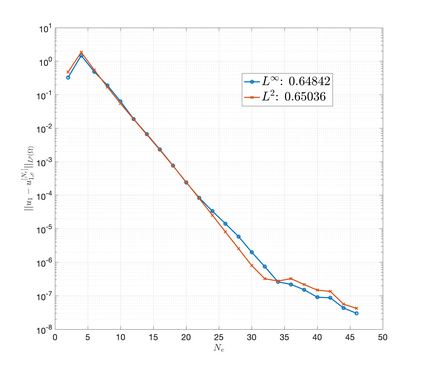
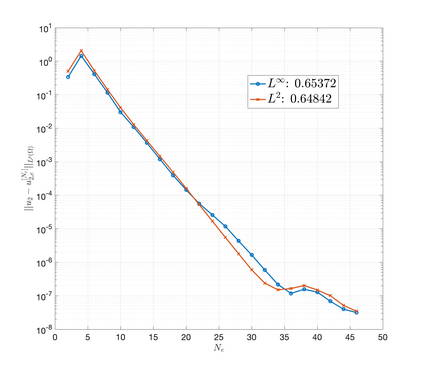
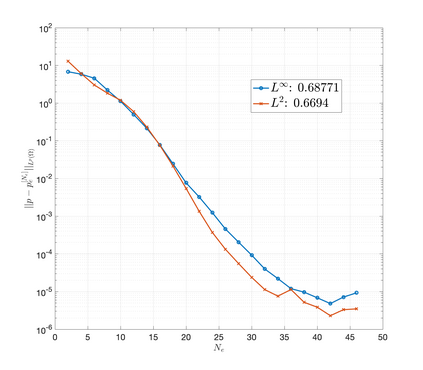
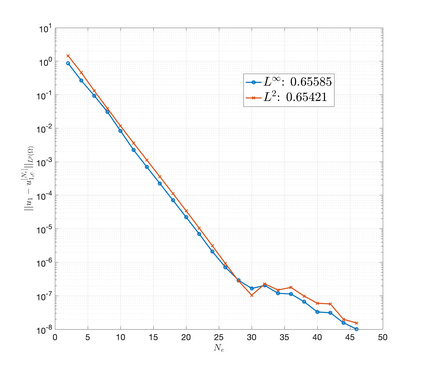
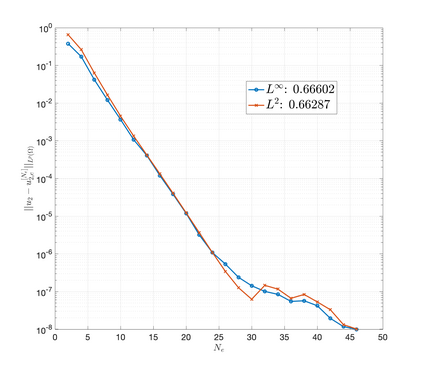
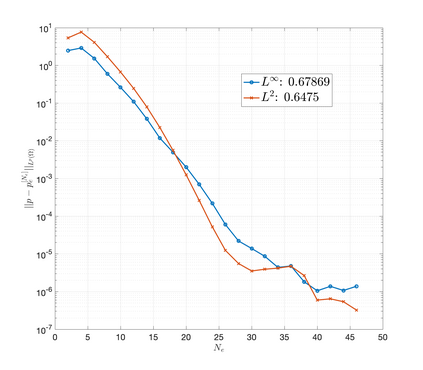
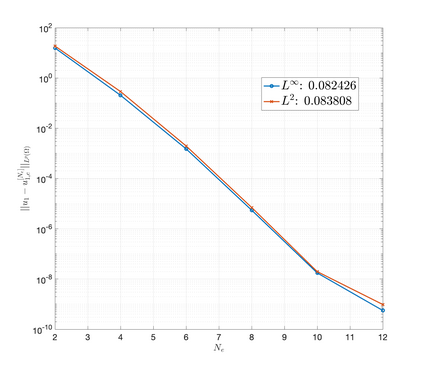
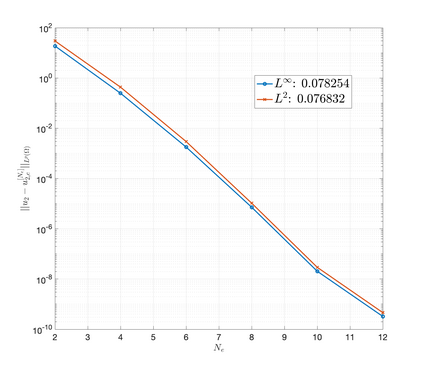
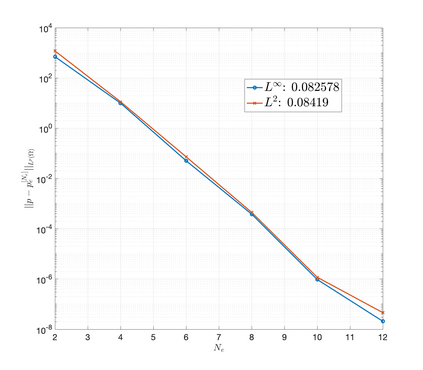
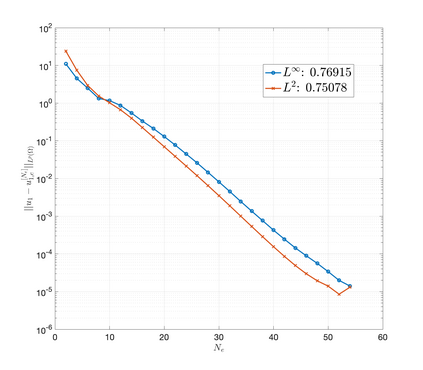
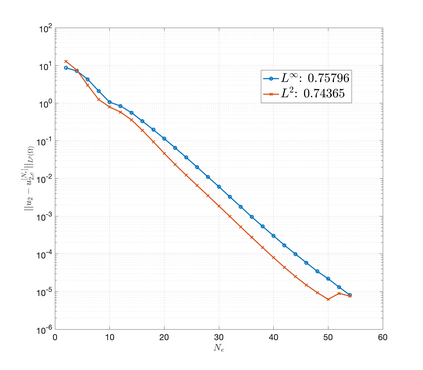
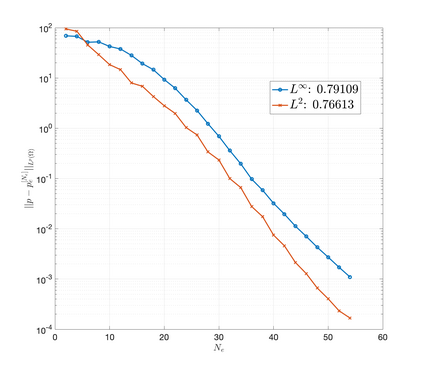
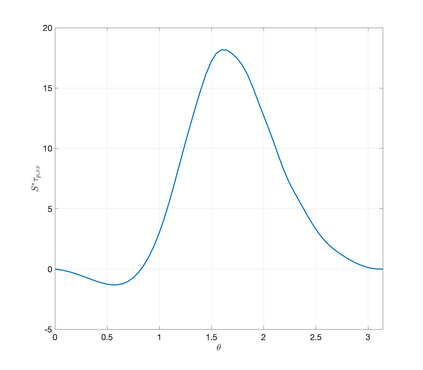
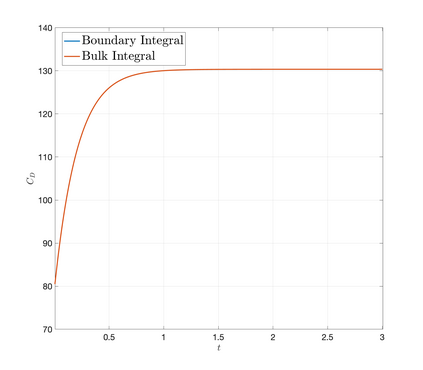
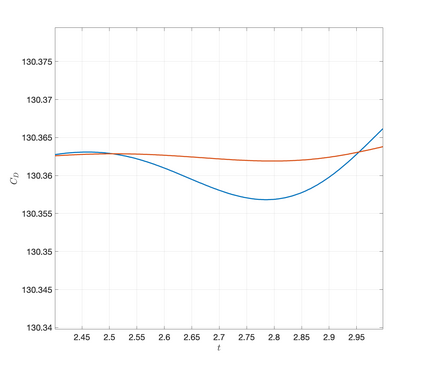
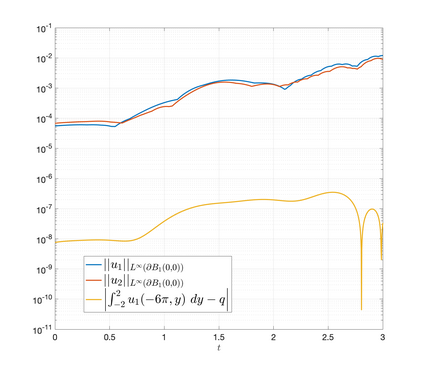
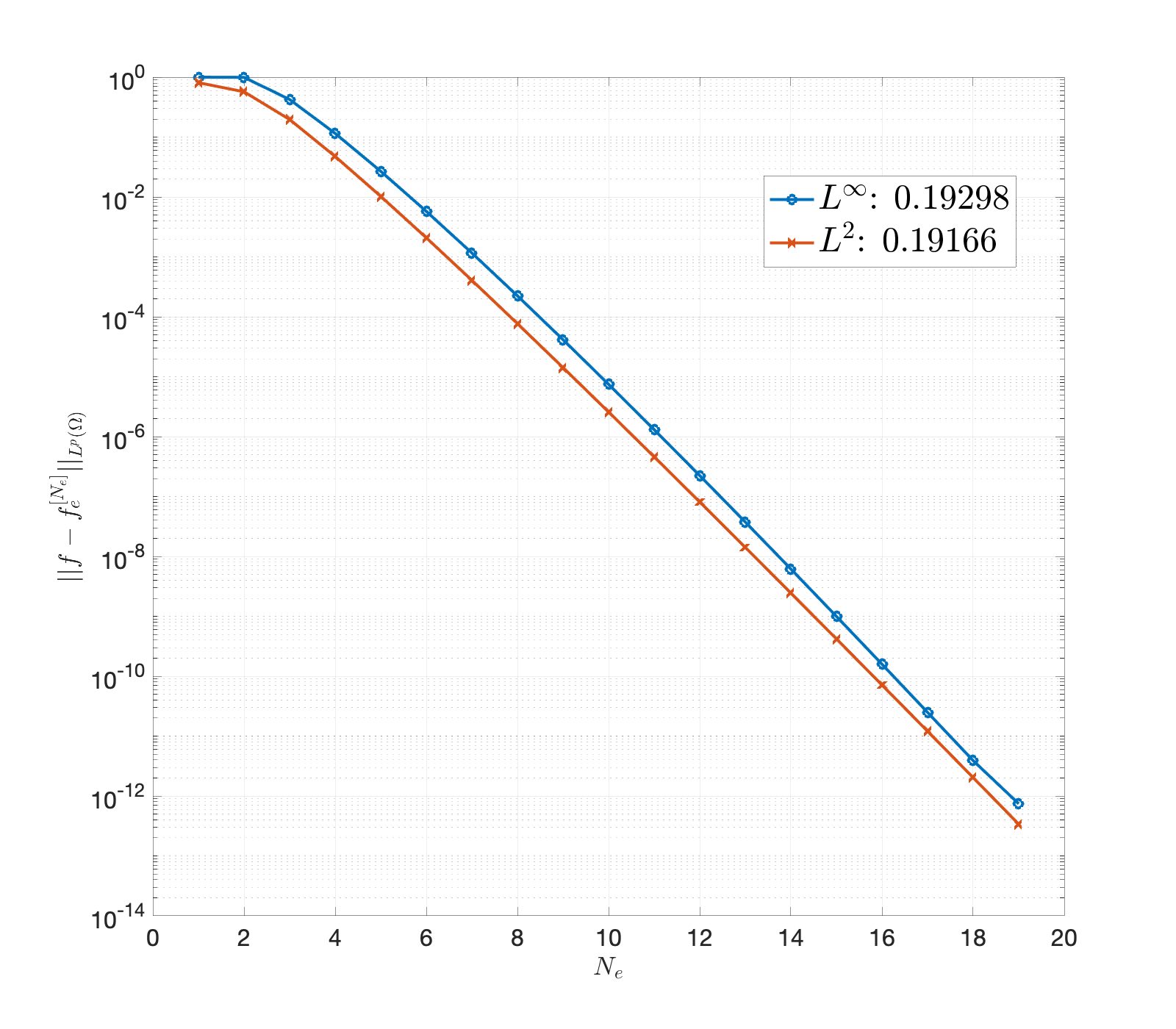
An essential ingredient of a spectral method is the choice of suitable bases for test and trial spaces. On complex domains, these bases are harder to devise, necessitating the use of domain partitioning techniques such as the spectral element method. In this study, we introduce the Projection Extension (PE) method, an approach that yields spectrally accurate solutions to various problems on complex geometries without requiring domain decomposition. This technique builds on the insights used by extension methodologies such as the immersed boundary smooth extension and Smooth Forcing Extension (SFE) methods that are designed to improve the order of accuracy of the immersed boundary method. In particular, it couples an accurate extension procedure, that functions on arbitrary domains regardless of connectedness or regularity, with a least squares minimization of the boundary conditions. The resulting procedure is stable under iterative application and straightforward to generalize to higher dimensions. Moreover, it rapidly and robustly yields exponentially convergent solutions to a number of challenging test problems, including elliptic, parabolic, Newtonian fluid flow, and viscoelastic problems.
翻译:光谱方法的一个基本成分是选择测试和试验空间的适当基础。 在复杂领域,这些基础较难设计,需要使用光谱元素法等域分隔技术。在本研究中,我们引入了投影扩展法(PE),这一方法可以产生对复杂地貌的各种问题的光谱准确的解决方案,而不需要域分解。这一技术以诸如浸入边界的平滑扩展法和平滑推进法(SFE)等延伸方法所使用的洞察力为基础,这些方法旨在提高浸入的边界方法的准确性。特别是,它结合了精确的扩展程序,即任意域的功能,而不论连接性或规律性,而边界条件最小化为平方最小。由此产生的程序在迭接应用下稳定,直通到更高的尺寸。此外,它迅速和稳健地产生对若干具有挑战性的试验问题,包括椭圆、抛物、牛顿流和粘结的液流和粘结问题。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem