Search of fractal space-filling curves with minimal dilation

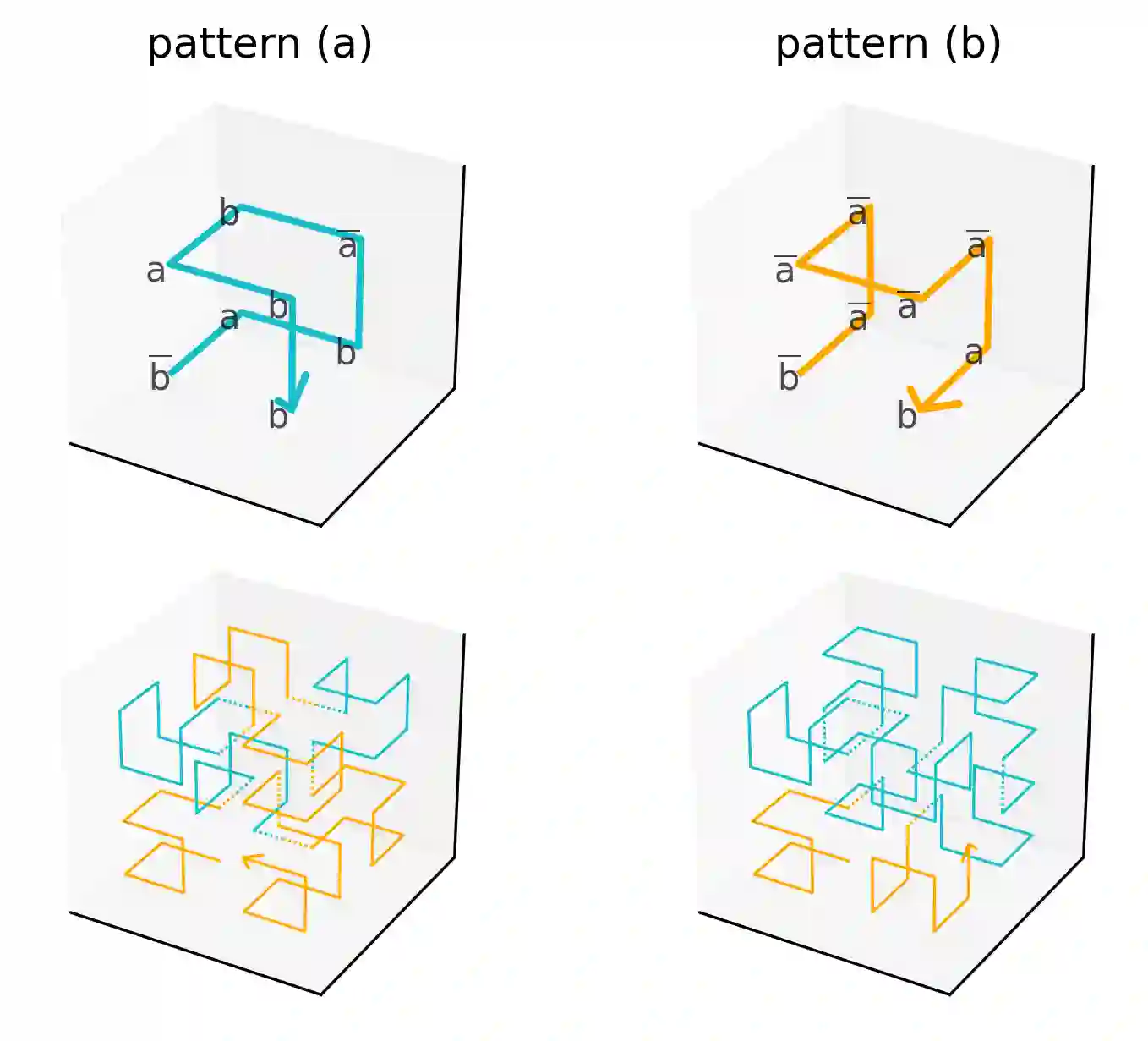
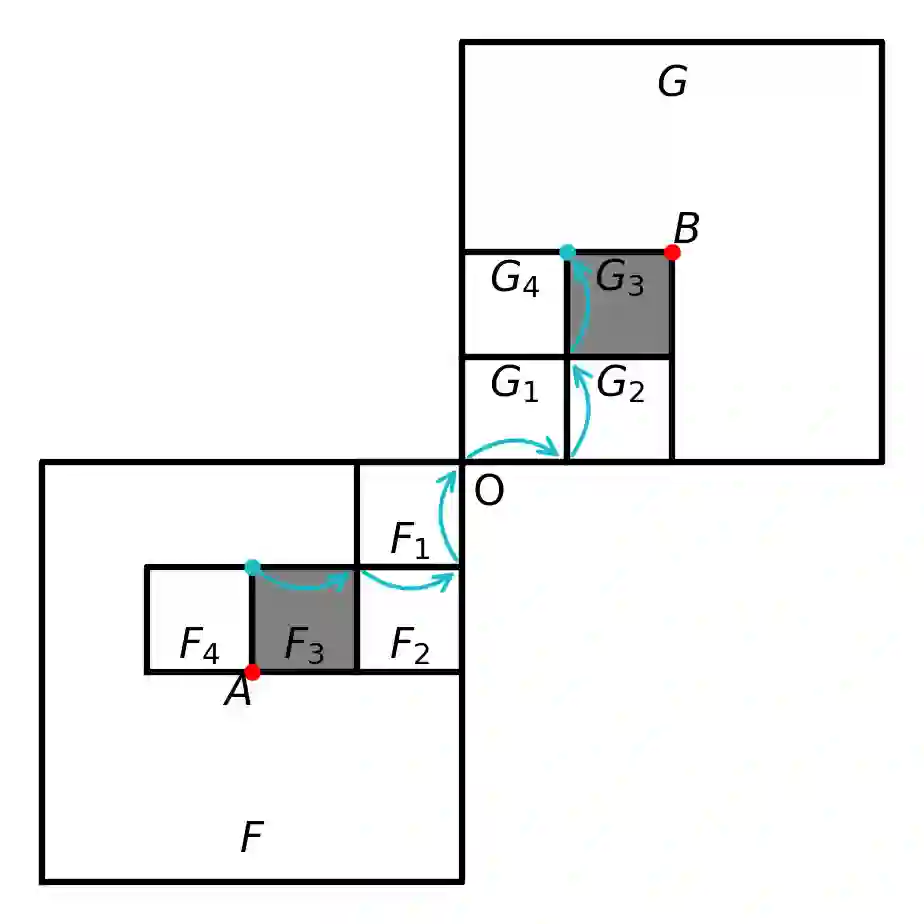
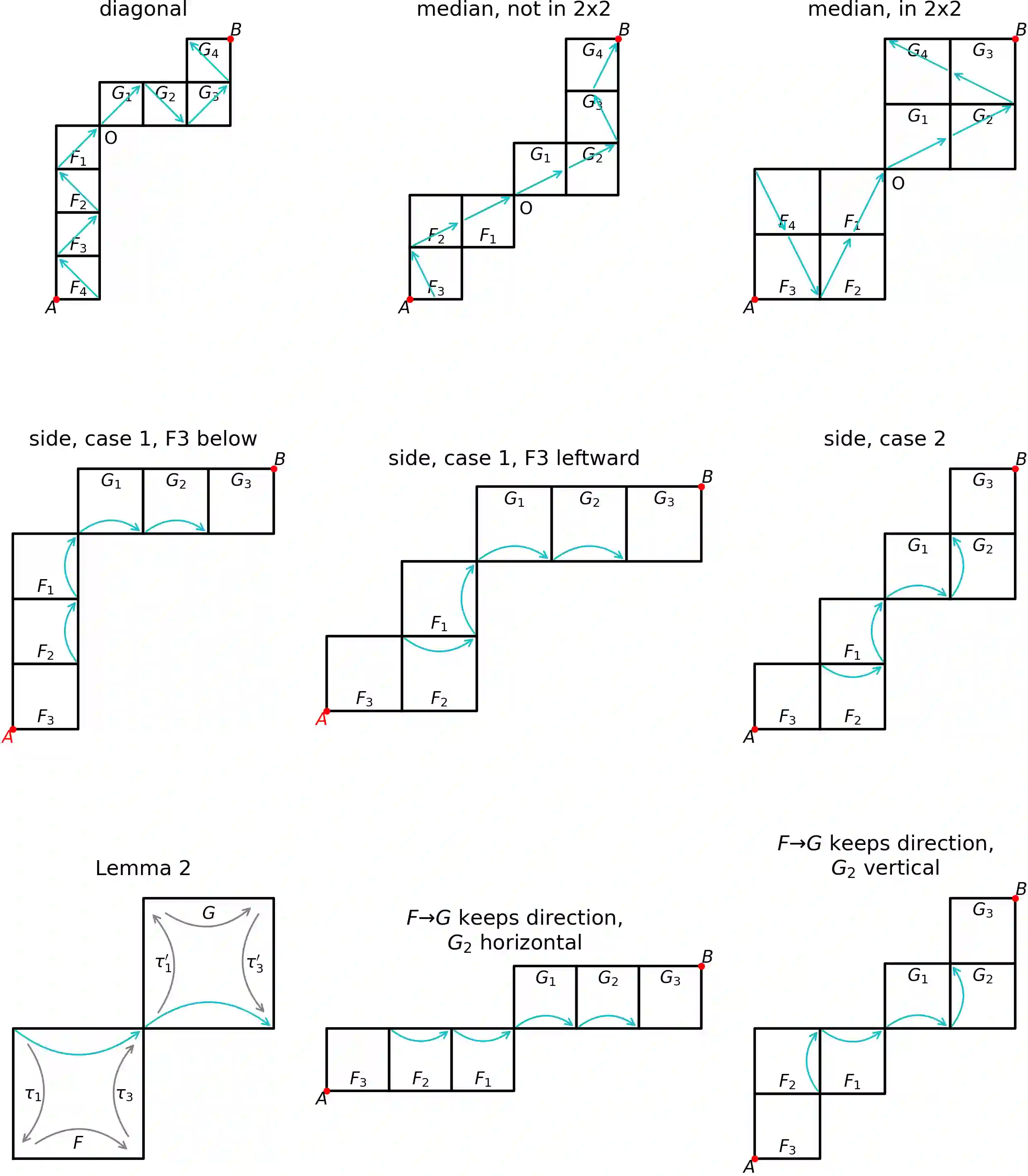
We introduce an algorithm for a search of extremal fractal curves in large curve classes. It heavily uses SAT-solvers -- heuristic algorithms that find models for CNF boolean formulas. Our algorithm was implemented and applied to the search of fractal surjective curves $\gamma\colon[0,1]\to[0,1]^d$ with minimal dilation $$\sup_{t_1<t_2}\frac{\|\gamma(t_2)-\gamma(t_1)\|^d}{t_2-t_1}.$$ We report new results of that search in the case of Euclidean norm. One of the results is a new curve that we call "YE", a self-similar (monofractal) plain curve of genus $5\times 5$ with dilation $5\frac{43}{73}=5.5890\ldots$, which is best-known among plain monofractals. Moreover, the YE-curve is the unique minimal curve among monofractals of genus $\le 6\times 6$. We give a proof of minimality, which relies both on computations and theoretical results. We notice that the classes of facet-gated multifractals are rigid enough to allow an efficient search, and contain many curves with small dilation. In dimension $3$ we have found facet-gated bifractals (that we call "Spring") of genus $2\times2\times 2$ with dilation $<17$. In dimension $4$ we obtained that there is a curve with dilation $<62$. Some lower bounds on the dilation for wider classes of cubically decomposable curves are proved.}