Learning differentiable solvers for systems with hard constraints

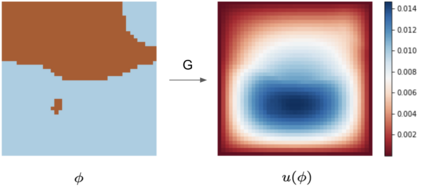
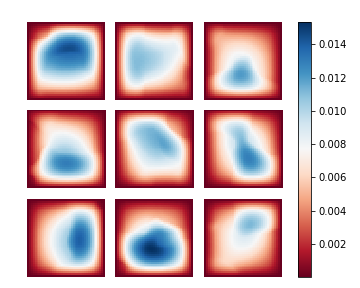
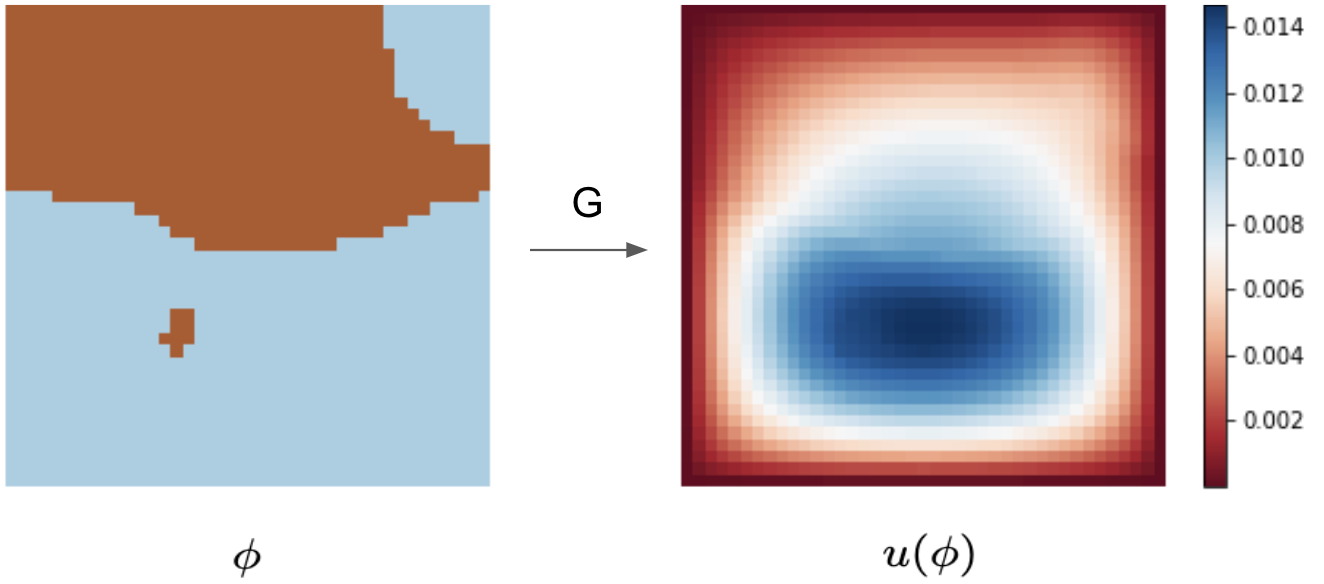
We introduce a practical method to enforce linear partial differential equation (PDE) constraints for functions defined by neural networks (NNs), up to a desired tolerance. By combining methods in differentiable physics and applications of the implicit function theorem to NN models, we develop a differentiable PDE-constrained NN layer. During training, our model learns a family of functions, each of which defines a mapping from PDE parameters to PDE solutions. At inference time, the model finds an optimal linear combination of the functions in the learned family by solving a PDE-constrained optimization problem. Our method provides continuous solutions over the domain of interest that exactly satisfy desired physical constraints. Our results show that incorporating hard constraints directly into the NN architecture achieves much lower test error, compared to training on an unconstrained objective.