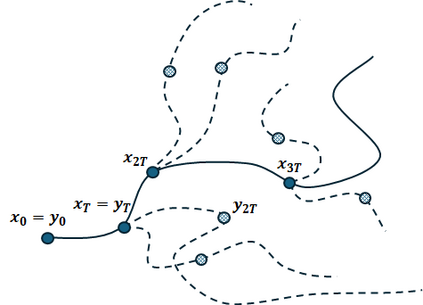
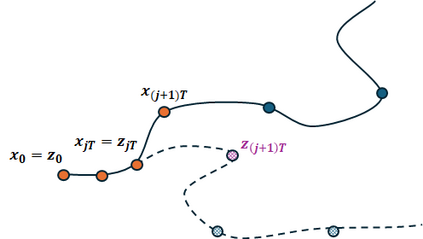
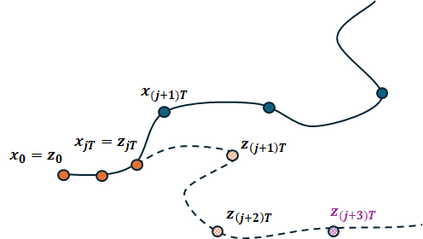
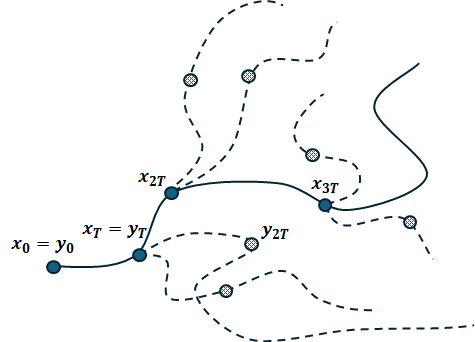
Local search is a powerful heuristic in optimization and computer science, the complexity of which has been studied in the white box and black box models. In the black box model, we are given a graph $G = (V,E)$ and oracle access to a function $f : V \to \mathbb{R}$. The local search problem is to find a vertex $v$ that is a local minimum, i.e. with $f(v) \leq f(u)$ for all $(u,v) \in E$, using as few queries to the oracle as possible. We show that if a graph $G$ admits a lazy, irreducible, and reversible Markov chain with stationary distribution $\pi$, then the randomized query complexity of local search on $G$ is $\Omega\left( \frac{\sqrt{n}}{t_{mix} \cdot \exp(3\sigma)}\right)$, where $t_{mix}$ is the mixing time of the chain and $\sigma = \max_{u,v \in V(G)} \frac{\pi(v)}{\pi(u)}.$ This theorem formally establishes a connection between the query complexity of local search and the mixing time of the fastest mixing Markov chain for the given graph. We also get several corollaries that lower bound the complexity as a function of the spectral gap, one of which slightly improves a lower bound based on spectral gaps from prior work.
翻译:暂无翻译