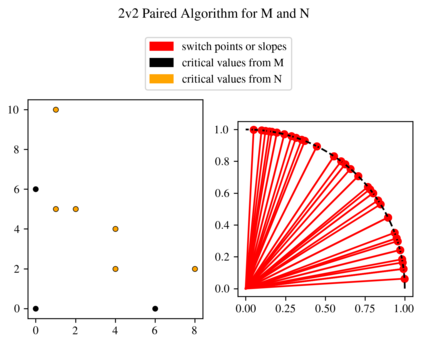
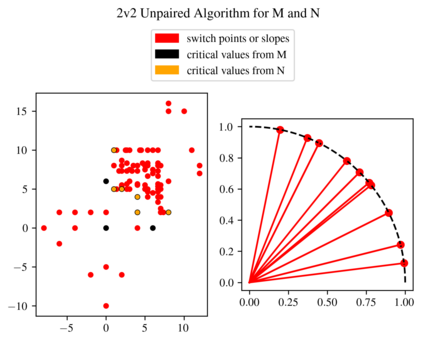
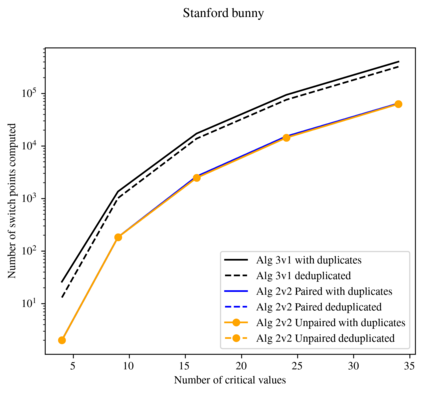
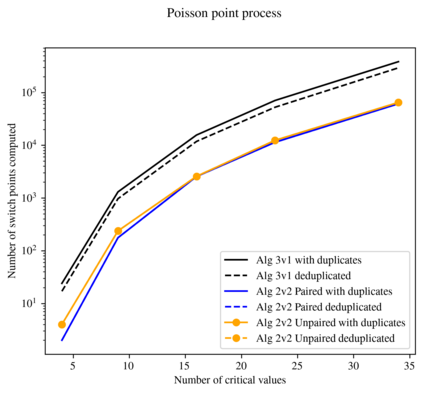
In multi-parameter persistence, the matching distance is defined as the supremum of weighted bottleneck distances on the barcodes given by the restriction of persistence modules to lines with a positive slope. In the case of finitely presented bi-persistence modules, all the available methods to compute the matching distance are based on restricting the computation to lines through pairs from a finite set of points in the plane. Some of these points are determined by the filtration data as they are entrance values of critical simplices. However, these critical values alone are not sufficient for the matching distance computation and it is necessary to add so-called switch points, i.e. points such that on a line through any of them, the bottleneck matching switches the matched pair. This paper is devoted to the algorithmic computation of the set of switch points given a set of critical values. We find conditions under which a candidate switch point is erroneous or superfluous. The obtained conditions are turned into algorithms that have been implemented. With this, we analyze how the size of the set of switch points increases as the number of critical values increases, and how it varies depending on the distribution of critical values. Experiments are carried out on various types of bi-persistence modules.
翻译:暂无翻译