Bias in Zipf's Law Estimators

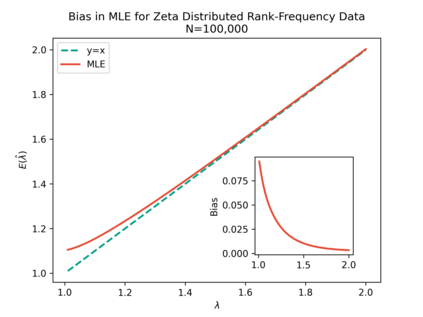
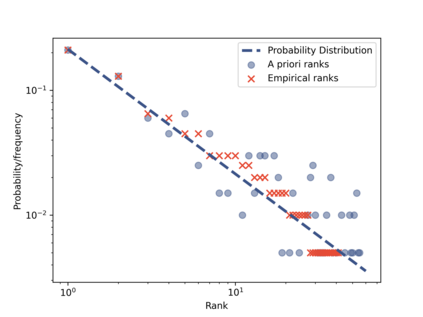
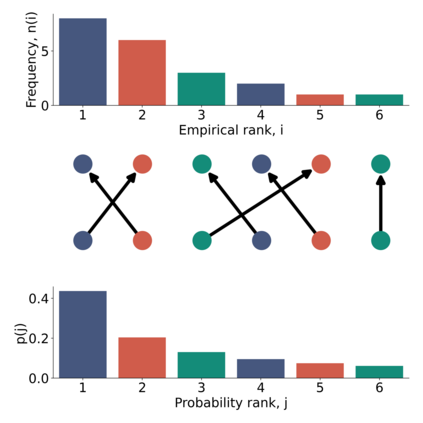
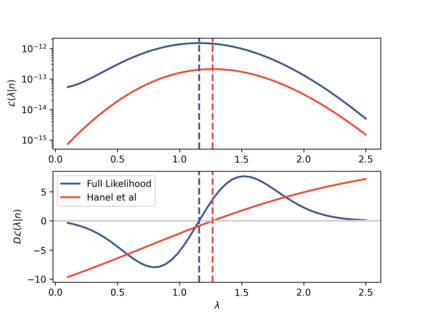
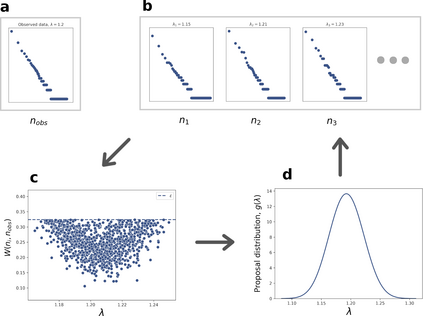
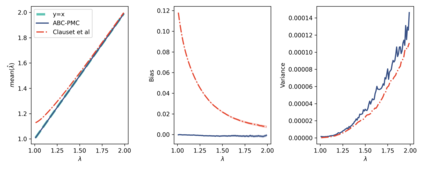
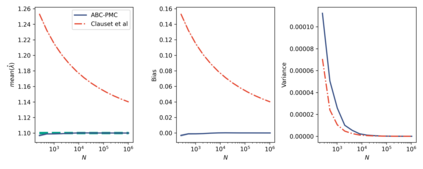
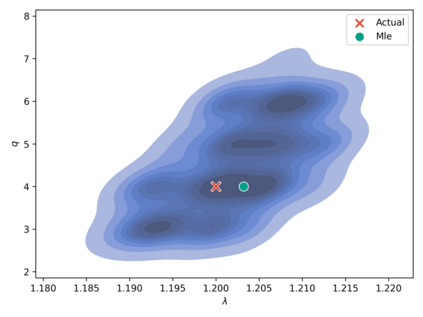
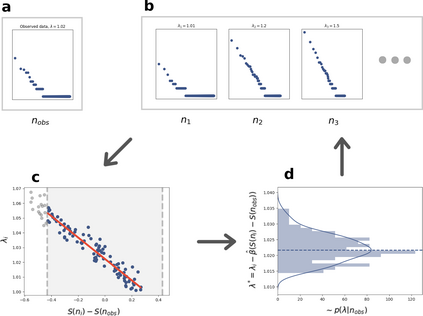
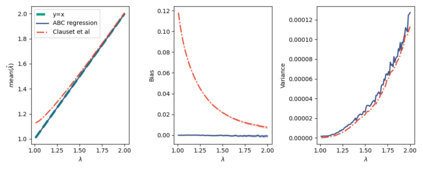
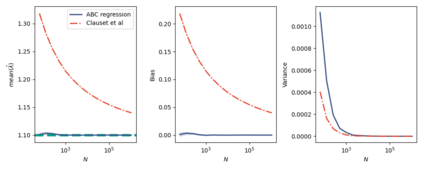
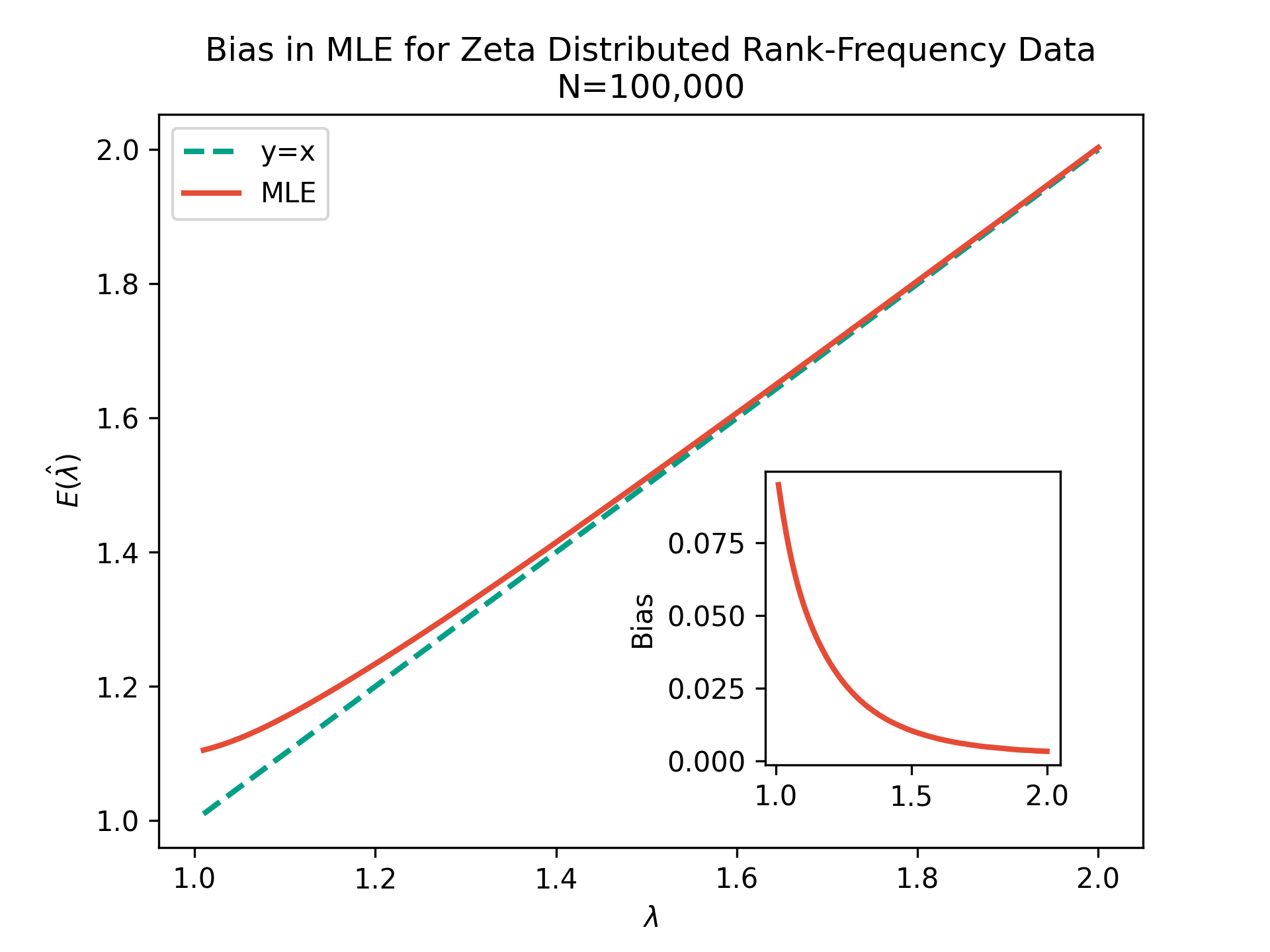
The prevailing maximum likelihood estimators for inferring power law models from rank-frequency data are biased. The source of this bias is an inappropriate likelihood function. The correct likelihood function is derived and shown to be computationally intractable. A more computationally efficient method of approximate Bayesian computation (ABC) is explored. This method is shown to have less bias for data generated from idealised rank-frequency Zipfian distributions. However, the existing estimators and the ABC estimator described here assume that words are drawn from a simple probability distribution, while language is a much more complex process. We show that this false assumption leads to continued biases when applying any of these methods to natural language to estimate Zipf exponents. We recommend caution when applying maximum likelihood estimation to investigate power laws in rank-frequency data, and suggest that researchers instead consider using graphical methods such as ordinary least squares and/or transform the data to a frequency-size representation.